forecast
Forecast conditional variances from conditional variance models
Syntax
Description
V = forecast(Mdl,numperiods,Y0)V of the fully
specified, univariate conditional variance model Mdl, over
a numperiods forecast horizon. The model
Mdl can be a garch, egarch, or gjr model object. The forecasts
represent the continuation of the conditional variances associated with the
presample data in the numeric array Y0.
Tbl2 = forecast(Mdl,numperiods,Tbl1)Tbl2 containing the paths of
MMSE conditional variance variable forecasts of the model
Mdl over a numperiods forecast
horizon. forecast uses the table or timetable of
presample data Tbl1 to initialize the response
series. (since R2023a)
To initialize the forecast, forecast selects the
response variable named in Mdl.SeriesName or the sole
variable in Tbl1. To select a different response variable
in Tbl1 to initialize the forecasts, use the
PresampleResponseVariable name-value argument.
[___] = forecast(___,
specifies options using one or more name-value arguments in
addition to any of the input argument combinations in previous syntaxes.
Name,Value)forecast returns the output argument combination for the
corresponding input arguments. For example, forecast(Mdl,10,Y0,V0=v0)
initializes the conditional variances for the forecast using the presample data
in v0.
Examples
Forecast the conditional variance of simulated data over a 30-period horizon. Supply a vector of presample response data.
Simulate 100 observations from a GARCH(1,1) model with known parameters.
Mdl = garch(Constant=0.02,GARCH=0.8,ARCH=0.1); rng("default") % For reproducibility [v,y] = simulate(Mdl,100);
Forecast the conditional variances over a 30-period horizon. Specify the simulated response data. Plot the forecasts.
vF = forecast(Mdl,30,y); figure plot(v,"-b") hold on plot(101:130,vF,"r--",LineWidth=2); title("Forecasted Conditional Variances") legend("Simulated presample","Forecasts") hold off

Forecasts converge asymptotically to the unconditional innovation variance.
Forecast the conditional variance of simulated data over a 30-period horizon.
Simulate 100 observations from an EGARCH(1,1) model with known parameters.
Mdl = egarch(Constant=0.01,GARCH=0.6,ARCH=0.2, ... Leverage=-0.2); rng("default") % For reproducibility [v,y] = simulate(Mdl,100);
Forecast the conditional variance over a 30-period horizon. Specify the simulated data as presample responses. Plot the forecasts.
VF1 = forecast(Mdl,30,y); figure plot(v,"r-") hold on plot(101:130,VF1,"b--",LineWidth=2); title("Forecasted Conditional Variances") legend("Simulated responses","Forecasts") hold off
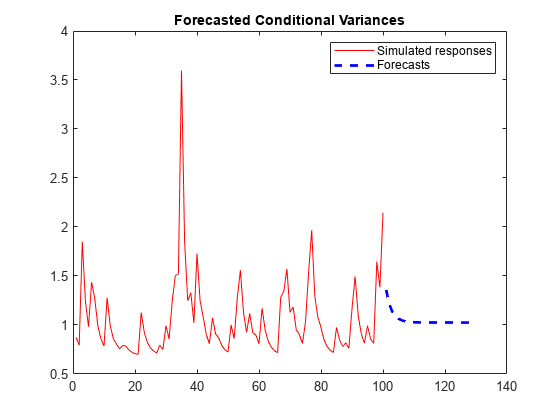
Forecast the conditional variance of simulated data over a 30-period horizon.
Simulate 100 observations from a GJR(1,1) model with known parameters.
Mdl = gjr(Constant=0.01,GARCH=0.6,ARCH=0.2, ... Leverage=0.2); rng("default") % For reproducibility [v,y] = simulate(Mdl,100);
Forecast the conditional variances over a 30-period horizon. Specify the simulated presample responses. Plot the forecasts.
vF = forecast(Mdl,30,y); figure plot(v,"r") hold on plot(101:130,vF,'b--',LineWidth=2); title("Forecasted Conditional Variances") legend("Observed","Forecasts") hold off

Since R2023a
Forecast the conditional variance of the average weekly closing NASDAQ returns from fitted GARCH(1,1), EGARCH(1,1) and GJR(1,1) models.
Load the U.S. equity indices data Data_EquityIdx.mat.
load Data_EquityIdxThe timetable DataTimeTable contains the daily NASDAQ closing prices, among other indices.
Compute the weekly average closing prices of all timetable variables.
DTTW = convert2weekly(DataTimeTable,Aggregation="mean");Compute the weekly percent returns and their sample mean.
DTTRet = price2ret(DTTW); DTTRet.Interval = []; DTTRet.NASDAQ = DTTRet.NASDAQ*100; T = height(DTTRet)
T = 626
meanRet = mean(DTTRet.NASDAQ)
meanRet = 0.0330
figure plot(DTTRet.Time,100*DTTRet.NASDAQ); hold on yline(100*meanRet,'--r') title("Daily NASDAQ Returns"); xlabel("Date"); ylabel("Return (%)");
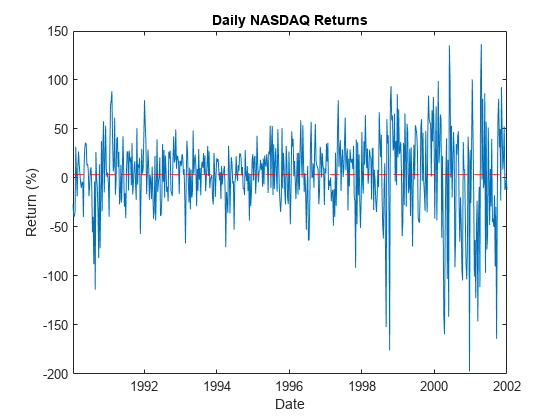
The variance of the series seems to change. This change is an indication of volatility clustering. The conditional mean model offset is very close to zero.
When you plan to supply a timetable, you must ensure it has all the following characteristics:
The selected response variable is numeric and does not contain any missing values.
The timestamps in the
Timevariable are regular, and they are ascending or descending.
Remove all missing values from the timetable, relative to the NASDAQ returns series.
DTTRet = rmmissing(DTTRet,DataVariables="NASDAQ");
numobs = height(DTTRet)numobs = 626
Because all sample times have observed NASDAQ returns, rmmissing does not remove any observations.
Determine whether the sampling timestamps have a regular frequency and are sorted.
areTimestampsRegular = isregular(DTTRet,"weeks")areTimestampsRegular = logical
1
areTimestampsSorted = issorted(DTTRet.Time)
areTimestampsSorted = logical
1
areTimestampsRegular = 1 indicates that the timestamps of DTTRet represent a regular weekly sample. areTimestampsSorted = 1 indicates that the timestamps are sorted.
Fit GARCH(1,1), EGARCH(1,1), and GJR(1,1) models to the data. By default, the software sets the conditional mean model offset to zero.
MdlGARCH = garch(1,1);
MdlEGARCH = egarch(1,1);
MdlGJR = gjr(1,1);
EstMdlGARCH = estimate(MdlGARCH,DTTRet,ResponseVariable="NASDAQ");
GARCH(1,1) Conditional Variance Model (Gaussian Distribution):
Value StandardError TStatistic PValue
_________ _____________ __________ ___________
Constant 0.0030629 0.0011827 2.5897 0.0096065
GARCH{1} 0.86501 0.02911 29.715 4.8912e-194
ARCH{1} 0.11835 0.024582 4.8144 1.4765e-06
EstMdlEGARCH = estimate(MdlEGARCH,DTTRet,ResponseVariable="NASDAQ");
EGARCH(1,1) Conditional Variance Model (Gaussian Distribution):
Value StandardError TStatistic PValue
_________ _____________ __________ __________
Constant -0.081262 0.030237 -2.6875 0.0071983
GARCH{1} 0.95557 0.01335 71.579 0
ARCH{1} 0.2768 0.052237 5.299 1.1645e-07
Leverage{1} -0.10519 0.025542 -4.1185 3.8142e-05
EstMdlGJR = estimate(MdlGJR,DTTRet,ResponseVariable="NASDAQ");
GJR(1,1) Conditional Variance Model (Gaussian Distribution):
Value StandardError TStatistic PValue
_________ _____________ __________ __________
Constant 0.0069063 0.0020036 3.447 0.0005668
GARCH{1} 0.78545 0.043862 17.907 1.0334e-71
ARCH{1} 0.090637 0.034313 2.6415 0.0082543
Leverage{1} 0.18663 0.054402 3.4305 0.0006025
Forecast the conditional variance for 20 weeks using the fitted models. Use the observed returns as presample innovations for the forecasts.
fh = 20; DTTVFGARCH = forecast(EstMdlGARCH,fh,DTTRet, ... PresampleResponseVariable="NASDAQ"); DTTVFEGARCH = forecast(EstMdlEGARCH,fh,DTTRet, ... PresampleResponseVariable="NASDAQ"); DTTVFGJR= forecast(EstMdlGJR,fh,DTTRet, ... PresampleResponseVariable="NASDAQ");
The forecasted conditional variance variables are called Y_Variance in each returned timetable.
Plot the forecasts along with the conditional variances inferred from the data.
DTTVGARCH = infer(EstMdlGARCH,DTTRet,ResponseVariable="NASDAQ"); DTTVEGARCH = infer(EstMdlEGARCH,DTTRet,ResponseVariable="NASDAQ"); DTTVGJR = infer(EstMdlGJR,DTTRet,ResponseVariable="NASDAQ"); figure tiledlayout(3,1) nexttile plot(DTTRet.Time(end-100:end),DTTVGARCH.Y_Variance(end-100:end), ... "r",DTTVFGARCH.Time,DTTVFGARCH.Y_Variance,"b--") legend("Inferred","Forecast",Location="northeast") title("GARCH(1,1) Conditional Variances") nexttile plot(DTTRet.Time(end-100:end),DTTVEGARCH.Y_Variance(end-100:end),"r", ... DTTVFEGARCH.Time,DTTVFEGARCH.Y_Variance,"b--") legend("Inferred","Forecast",Location="northeast") title("EGARCH(1,1) Conditional Variances") nexttile plot(DTTRet.Time(end-100:end),DTTVGJR.Y_Variance(end-100:end),"r", ... DTTVFGJR.Time,DTTVFGJR.Y_Variance,'b--') legend("Inferred","Forecast",Location="northeast") title("GJR(1,1) Conditional Variances")
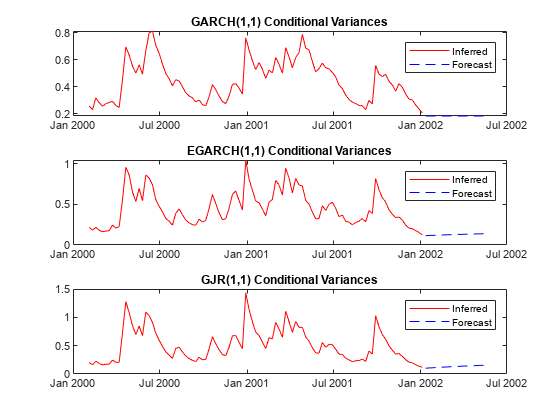
Plot conditional variance forecasts for the next 500 weeks after the sample.
fh = 500; DTTVF1000GARCH = forecast(EstMdlGARCH,fh,DTTRet, ... PresampleResponseVariable="NASDAQ"); DTTVF1000EGARCH = forecast(EstMdlEGARCH,fh,DTTRet, ... PresampleResponseVariable="NASDAQ"); DTTVF1000GJR= forecast(EstMdlGJR,fh,DTTRet, ... PresampleResponseVariable="NASDAQ"); figure plot(DTTVF1000GARCH.Time,DTTVF1000GARCH.Y_Variance,'b',... DTTVF1000EGARCH.Time,DTTVF1000EGARCH.Y_Variance,'r',... DTTVF1000GJR.Time,DTTVF1000GJR.Y_Variance,'k') legend("GARCH Forecast","EGARCH Foecast","GJR Forecast",Location="northeast") title("Long-Run Conditional Variance Forecast")
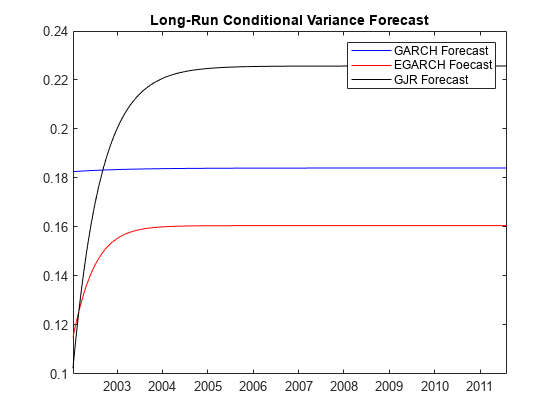
The forecasts converge asymptotically to the unconditional variances of their respective processes.
Input Arguments
Forecast horizon, or the number of time points in the forecast period, specified as a positive integer.
Data Types: double
Presample response data yt used
to infer presample innovations εt,
and whose conditional variance process
σt2
is forecasted, specified as a numpreobs-by-1 numeric
column vector or a
numpreobs-by-numpaths numeric
matrix. When you supply Y0, supply all optional data as
numeric arrays, and forecast returns results in
numeric arrays.
numpreobs is the number of presample
observations.
Y0 can represent a mean 0 presample innovations series
with a variance process characterized by the conditional variance model
Mdl. Y0 can also represent a
presample innovations series plus an offset (stored in
Mdl.Offset). For more details, see Algorithms.
Each row is a presample observation, and measurements in each row occur
simultaneously. The last row contains the latest presample observation.
numpreobs must be at least Mdl.Q
to initialize the conditional variance model. If
numpreobs > Mdl.Q,
forecast uses only the latest
Mdl.Q rows. For more details, see Time Base Partitions for Forecasting.
Columns of Y0 correspond to separate, independent
paths.
If
Y0is a column vector, it represents a single path of the response series.forecastapplies it to each forecasted path. In this case, all forecast pathsYderive from the same initial responses.If
Y0is a matrix, each column represents a presample path of the response series.numpathsis the maximum among the second dimensions of the specified presample observation matricesY0andV0.
Data Types: double
Since R2023a
Presample data containing the response variable
yt and, optionally, the
conditional variance variable
σt2
used to initialize the model for the forecast, specified as a table or
timetable, the same type as Tbl1, with
numprevars variables and numpreobs
rows. You can select a response variable or conditional variance variable
from Tbl1 by using the
PresampleResponseVariable or
PresampleVarianceVariable name-value argument,
respectively.
Each selected variable is single path (numpreobs-by-1
vector) or multiple paths
(numpreobs-by-numpaths matrix) of
presample response or conditional variance data. Each row is a presample
observation, and measurements in each row occur simultaneously.
numpreobs must be one of the following values:
Mdl.QwhenTbl1provides only presample responsesmax([Mdl.P Mdl.Q])whenTbl1also provides presample conditional variances
If you supply more rows than necessary,
forecast uses the latest required number of
observations only.
If Tbl1 is a timetable, all the following conditions
must be true:
Tbl1must represent a sample with a regular datetime time step (seeisregular).The datetime vector of sample timestamps
Tbl1.Timemust be ascending or descending.
If Tbl1 is a table, the last row contains the latest
presample observation.
Although forecast requires presample response
data, forecast sets default presample conditional
variance data in one of the following ways:
If
numpreobs≥max([Mdl.P Mdl.Q]) + Mdl.P,forecastinfers presample conditional variances from the presample response data (seeinfer).Otherwise:
If
Mdlis a GARCH(P,Q) or GJR(P,Q) model,forecastsets all required conditional variances to the unconditional variance of the conditional variance process.If
Mdlis a EGARCH(P,Q) model,forecastsets all required conditional variances to the exponentiated, unconditional mean of the logarithm of the EGARCH(P,Q) variance process.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: forecast(Mdl,10,Y0,V0=[1 0.5;1 0.5]) specifies two
different presample paths of conditional variances.
Presample conditional variances
σt2
used to initialize the conditional variance model, specified as a
numpreobs-by-1 positive column vector or
numpreobs-by-numpaths positive
matrix. Use V0 only when you supply the numeric array
of presample response data Y0.
Rows of V0 correspond to periods in the presample,
and the last row contains the latest presample conditional variance.
For GARCH(P,Q) and GJR(P,Q) models,
numpreobsmust be at leastMdl.Pto initialize the variance equation.For EGARCH(P,Q) models,
numpreobsmust be at leastmax([Mdl.P Mdl.Q])to initialize the variance equation.
If numpreobs exceeds the minimum number,
forecast uses only the latest
observations.
Columns of V0 correspond to separate, independent paths.
If
V0is a column vector,forecastapplies it to each forecasted path. In this case, the conditional variance model of all forecast pathsVderives from the same initial conditional variances.If
V0is a matrix, it must havenumpathscolumns, the same number of columns asY0.
forecast sets default presample conditional
variance data in one of the following ways:
If the number of rows of
Y0numpreobs≥max([Mdl.P Mdl.Q]) + Mdl.P,forecastinfersV0fromY0(seeinfer).Otherwise:
If
Mdlis a GARCH(P,Q) or GJR(P,Q) model,forecastsets all required conditional variances to the unconditional variance of the conditional variance process.If
Mdlis a EGARCH(P,Q) model,forecastsets all required conditional variances to the exponentiated, unconditional mean of the logarithm of the EGARCH(P,Q) variance process.
Data Types: double
Since R2023a
Variable of Tbl1 containing presample response
paths yt, specified as one of
the following data types:
String scalar or character vector containing a variable name in
Tbl1.Properties.VariableNamesVariable index (integer) to select from
Tbl1.Properties.VariableNamesA length
numprevarslogical vector, wherePresampleResponseVariable(selects variablej) = truejTbl1.Properties.VariableNames, andsum(PresampleResponseVariable)is1
The selected variable must be a numeric matrix and cannot contain
missing values (NaN).
If Tbl1 has one variable, the default specifies
that variable. Otherwise, the default matches the variable to name in
Mdl.SeriesName.
Example: PresampleResponseVariable="StockRate"
Example: PresampleResponseVariable=[false false true
false] or PresampleResponseVariable=3
selects the third table variable as the presample response
variable.
Data Types: double | logical | char | cell | string
Since R2023a
Variable of Tbl1 containing presample conditional
variance paths
σt2,
specified as one of the following data types:
String scalar or character vector containing a variable name in
Tbl1.Properties.VariableNamesVariable index (integer) to select from
Tbl1.Properties.VariableNamesA length
numprevarslogical vector, wherePresampleVarianceVariable(selects variablej) = truejTbl1.Properties.VariableNames, andsum(PresampleVarianceVariable)is1
The selected variable must be a numeric vector and cannot contain
missing values (NaN).
To use presample conditional variance data in
Tbl1, you must specify
PresampleVarianceVariable.
Example: PresampleVarianceVariable="StockRateVar"
Example: PresampleVarianceVariable=[false false true
false] or PresampleVarianceVariable=3
selects the third table variable as the presample conditional variance
variable.
Data Types: double | logical | char | cell | string
Note
NaNvalues in numeric presample data setsY0andV0indicate missing data.forecastremoves missing data from the presample data sets following this procedure:forecasthorizontally concatenatesY0andV0such that the latest observations occur simultaneously. The result can be a jagged array because the presample data sets can have a different number of rows. In this case,forecastprepads variables with an appropriate amount of zeros to form a matrix.forecastapplies list-wise deletion to the combined presample matrix by removing all rows containing at least oneNaN.forecastextracts the processed presample data sets from the result of step 2, and removes all prepadded zeros.
List-wise deletion reduces the sample size and can create irregular time series.
For numeric data inputs,
forecastassumes that you synchronize the presample data such that the latest observations occur simultaneously.forecastissues an error when any table or timetable input contains missing values.
Output Arguments
Paths of MMSE forecasts of conditional variances
σt2
of future model innovations εt,
returned as a numperiods-by-1 numeric column vector or
a numperiods-by-numpaths numeric
matrix. forecast returns V only
when you supply the input Y0.
V represents a continuation of V0
(V(1,:) occurs in the next time point after
V0(end,:)).
V(
contains the j,k)j-period-ahead forecasted
conditional variance of path k.
forecast determines numpaths
from the number of columns in the presample data sets
Y0 and V0. For details, see
Algorithms. If each
presample data set has one column, then V is a column
vector.
Since R2023a
Paths of MMSE forecasts of conditional variances
σt2
of future model innovations εt,
returned as a table or timetable, the same data type as
Tbl1. forecast returns
Tbl2 only when you supply the input
Tbl1.
Tbl2 contains a variable for all forecasted conditional
variance paths, which are in a
numperiods-by-numpaths numeric
matrix, with rows representing periods in the forecast horizon and columns
representing independent paths, each corresponding to the input presample
response and conditional variance paths in Tbl1.
forecast names the forecasted conditional
variance variable in Tbl2
responseName_VarianceresponseNameMdl.SeriesName. For example, if
Mdl.SeriesName is StockReturns,
Tbl2 contains a variable for the corresponding
forecasted conditional variance paths with the name
StockReturns_Variance.
Tbl2.
represents a continuation of the presample conditional variance process,
either supplied by responseName_VarianceTbl1 or set by default
(Tbl2.
occurs in the next time point, with respect to the periodicity
responseName_Variance(1,:)Tbl1, after the last presample conditional
variance).
Tbl2.
contains the responseName_Variance(j,k)j-period-ahead forecasted
conditional variance of path k.
If Tbl1 is a timetable, the following conditions hold:
The row order of
Tbl2, either ascending or descending, matches the row order ofTbl1.Tbl2.Time(1)is the next time afterTbl1.Time(end)relative the sampling frequency, andTbl2.Time(2:numobs)are the following times relative to the sampling frequency.
More About
Time base partitions for forecasting are
two disjoint, contiguous intervals of the time base; each interval contains time
series data for forecasting a dynamic model. The forecast
period (forecast horizon) is a numperiods
length partition at the end of the time base during which
forecast generates forecasts V from
the dynamic model Mdl. The presample
period is the entire partition occurring before the forecast period.
forecast can require observed responses (or innovations)
Y0 or conditional variances V0 in the
presample period to initialize the dynamic model for forecasting. The model
structure determines the types and amounts of required presample
observations.
A common practice is to fit a dynamic model to a portion of the data set, then
validate the predictability of the model by comparing its forecasts to observed
responses. During forecasting, the presample period contains the data to which the
model is fit, and the forecast period contains the holdout sample for validation.
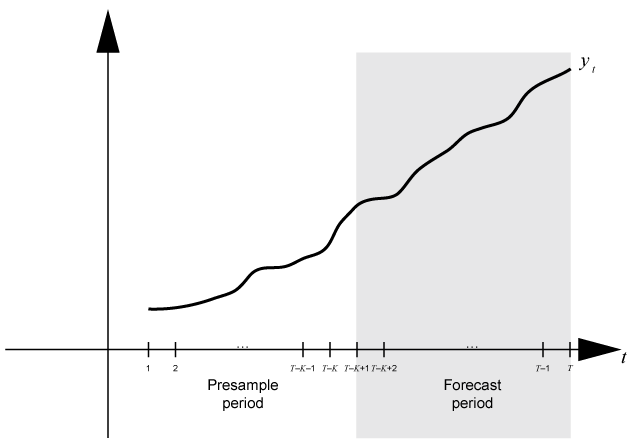
Suppose that yt is an observed response
series. Consider forecasting conditional variances from a dynamic model of
yt
numperiods = K periods. Suppose that the
dynamic model is fit to the data in the interval [1,T –
K] (for more details, see estimate). This figure shows the time base partitions for
forecasting.
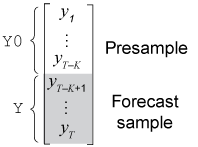
For example, to generate forecasts Y from a GARCH(0,2) model,
forecast requires presample responses (innovations)
Y0 = to initialize the model. The 1-period-ahead forecast requires both
observations, whereas the 2-periods-ahead forecast requires
yT –
K and the 1-period-ahead forecast
V(1). forecast generates all other
forecasts by substituting previous forecasts for lagged responses in the
model.
Dynamic models containing a GARCH component can require presample conditional
variances. Given enough presample responses, forecast infers
the required presample conditional variances. This figure shows the arrays of
required observations for this case, with corresponding input and output
arguments.
Algorithms
If the conditional variance model
Mdlhas an offset (Mdl.Offset),forecastsubtracts it from the specified presample responses to obtain presample innovations. Subsequently,forecastuses to initialize the conditional variance model for forecasting.forecastsets the number of sample paths to forecastnumpathsto the maximum number of columns among the specified presample response and conditional variance data sets. All presample data sets must have eithernumpaths> 1 columns or one column. Otherwise,forecastissues an error. For example, ifY0has five columns, representing five paths, thenV0can either have five columns or one column. IfV0has one column, thenforecastappliesV0to each path.
References
[1] Bollerslev, T. “Generalized Autoregressive Conditional Heteroskedasticity.” Journal of Econometrics. Vol. 31, 1986, pp. 307–327.
[2] Bollerslev, T. “A Conditionally Heteroskedastic Time Series Model for Speculative Prices and Rates of Return.” The Review of Economics and Statistics. Vol. 69, 1987, pp. 542–547.
[3] Box, G. E. P., G. M. Jenkins, and G. C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.
[4] Enders, W. Applied Econometric Time Series. Hoboken, NJ: John Wiley & Sons, 1995.
[5] Engle, R. F. “Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation.” Econometrica. Vol. 50, 1982, pp. 987–1007.
[6] Glosten, L. R., R. Jagannathan, and D. E. Runkle. “On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks.” The Journal of Finance. Vol. 48, No. 5, 1993, pp. 1779–1801.
[7] Hamilton, J. D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[8] Nelson, D. B. “Conditional Heteroskedasticity in Asset Returns: A New Approach.” Econometrica. Vol. 59, 1991, pp. 347–370.
Version History
Introduced in R2012aIn addition to accepting input presample data in numeric arrays,
forecast accepts input data in tables or regular
timetables. When you supply data in a table or timetable, the following conditions
apply:
forecastchooses the default series on which to operate, but you can use the specified optional name-value argument to select a different variable.forecastreturns results in a table or timetable.
Name-value arguments to support tabular workflows include:
PresampleResponseVariablespecifies the variable name of the response paths in the input presample dataTbl1to initialize the response series for the forecast.PresampleVarianceVariablespecifies the variable name of the conditional variance paths in the input presample dataTbl1to initialize the conditional variance series for the forecast.
forecast now has a third input argument for you to supply
presample response data.
forecast(Mdl,numperiods,Y0) forecast(Mdl,numperiods,Y0,Name,Value)
Before R2019a, the syntaxes were:
forecast(Mdl,numperiods) forecast(Mdl,numperiods,Name,Value)
Y0
name-value argument.There are no plans to remove the previous syntaxes or the Y0
name-value argument at this time. However, you are encouraged to supply presample
responses because, to forecast conditional variances from a conditional variance
model, forecast must initialize models containing lagged
variables. Without specified presample responses, forecast
initializes models by using reasonable default values, but the default might not
support all workflows. This table describes the default values for each conditional
variance model object.
| Model Object | Presample Default |
|---|---|
garch | All presample responses are the unconditional standard deviation of the process. |
egarch | All presample responses are 0. |
gjr | All presample responses are the unconditional standard deviation of the process. |
Update your code by specifying presample response data in the third input argument.
If you do not supply presample responses, forecast
provides default presample values that might not support all workflows.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)