hpfilter

Hodrick-Prescott filter for trend and cyclical components

Syntax

[Trend,Cyclical] = hpfilter(Y)

[TTbl,CTbl] = hpfilter(Tbl)

[___] = hpfilter(___,Name=Value)

hpfilter(___)

hpfilter(ax,___)

[___,h] = hpfilter(___)

Description

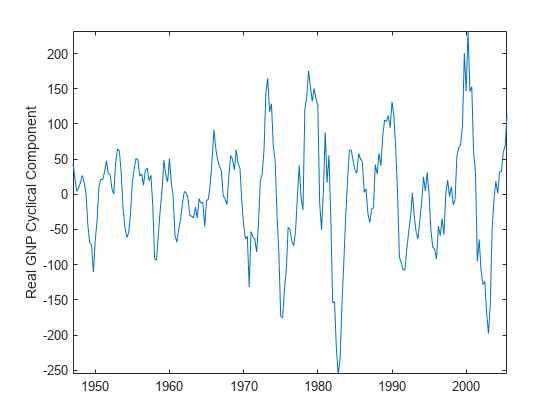
The hpfilter function applies the Hodrick-Prescott filter to separate one or more time series into additive trend and cyclical components. hpfilter optionally plots the series and trend component, with cycles removed. The plot helps you select a smoothing parameter.

In addition to the Hodrick-Prescott filter, Econometrics Toolbox™ supports the Baxter-King (bkfilter), Christiano-Fitzgerald (cffilter), and Hamilton (hfilter) filters.

[Trend,Cyclical] = hpfilter(Y) returns the additive trend and cyclical components from applying the Hodrick-Prescott filter [1] to each variable (column) of the input matrix of time series data. The smoothing parameter default is 1600, suggested in [1] for quarterly data.

[TTbl,CTbl] = hpfilter(Tbl) returns tables or timetables containing variables for the trend and cyclical components from applying the Hodrick-Prescott filter to each variable in the input table or timetable. To select different variables to filter, use the DataVariables name-value argument. (since R2022a)

[___] = hpfilter(___,Name=Value) specifies options using one or more name-value arguments in addition to any of the input argument combinations in previous syntaxes. hpfilter returns the output argument combination for the corresponding input arguments. For example, hpfilter(Tbl,Smoothing=100,DataVariables=1:5) applies the Hodrick-Prescott filter to the first five variables in the input table Tbl and sets the smoothing parameter to 100. (since R2022a)

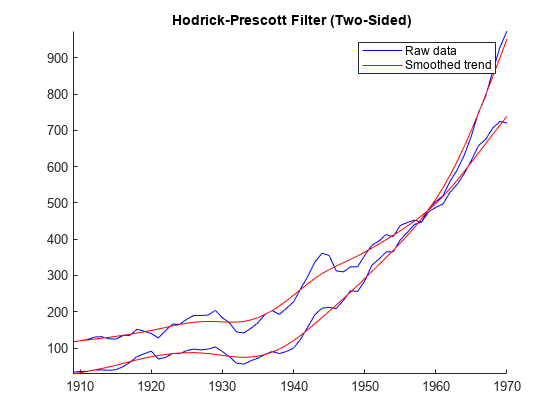
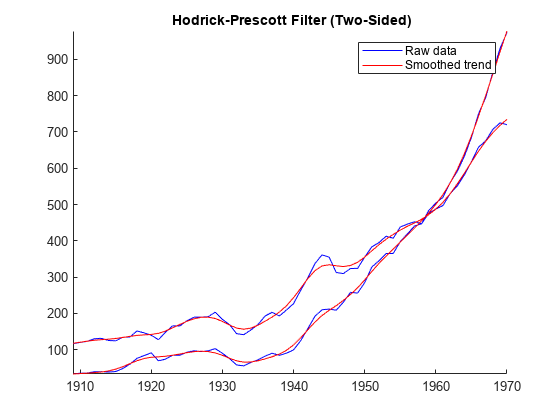
hpfilter(___) plots time series variables in the input data and their respective trend components, computed by the Hodrick-Prescott filter, on the same axes.

hpfilter(ax,___) plots on the axes specified by ax instead of the current axes (gca). ax can precede any of the input argument combinations in the previous syntaxes. (since R2022a)

[___,h] = hpfilter(___) plots the specified series and their trend components, and additionally returns handles to plotted graphics objects. Use elements of h to modify properties of the plot after you create it. (since R2022a)

Examples

Apply Hodrick-Prescott Filter to Matrix of Data

Plot the cyclical component of the US post-WWII, seasonally adjusted, quarterly, real gross national product (GNPR).

load Data_GNP
GNPR = Data(:,2);
[trend,cyclical] = hpfilter(GNPR);
T = numel(trend)

T = 
235

trend and cyclical are 235-by-1 vectors containing the trend and cyclical components, respectively, resulting from applying the Hodrick-Prescott filter to the series with default smoothing parameter 1600.

plot(dates,cyclical) 
axis tight
ylabel("Real GNP Cyclical Component")

Apply Hodrick-Prescott Filter to Table Variables

Since R2022a

Apply the Hodrick-Prescott filter to all variables in input table variables.

Load the Schwert stock data set Data_SchwertStock.mat, which contains monthly returns of the NYSE index from 1871 through 2008 in DataTimeTableMth, among three other variables (for details, enter Description). Remove all missing observations from all series.

load Data_SchwertStock
TTM = rmmissing(DataTimeTableMth);

Aggregate the monthly data in the timetable to quarterly measurements.

TTQ = convert2quarterly(TTM);

Apply the Hodrick-Prescott filter to all variables in the quarterly timetable. The default smoothing parameter value is 1600. Display the last few observed components.

[TQTT,CQTT] = hpfilter(TTQ);
size(TQTT)

ans = 1×2

   220     4

tail(TQTT)

       Time         Return       DivYld        CapGain       CapGainA  
    ___________    _________    _________    ___________    ___________

    31-Mar-1924    0.0046179    0.0067678     -0.0021499     -0.0021499
    30-Jun-1924     0.005586    0.0067204     -0.0011344     -0.0011344
    30-Sep-1924    0.0066431    0.0066689    -2.5812e-05    -2.5812e-05
    31-Dec-1924    0.0077772    0.0066142      0.0011629      0.0011629
    31-Mar-1925    0.0089687    0.0065574      0.0024113      0.0024113
    30-Jun-1925     0.010231    0.0064998      0.0037314      0.0037314
    30-Sep-1925     0.011543    0.0064423      0.0051005      0.0051005
    31-Dec-1925     0.012878    0.0063854      0.0064922      0.0064922

tail(CQTT)

       Time          Return        DivYld        CapGain       CapGainA 
    ___________    __________    ___________    __________    __________

    31-Mar-1924     -0.019683     0.00033141     -0.020014     -0.020014
    30-Jun-1924      0.059151     5.7125e-05      0.059093      0.059093
    30-Sep-1924     -0.011788     0.00044598     -0.012234     -0.012234
    31-Dec-1924      0.052846     0.00052627       0.05232       0.05232
    31-Mar-1925     -0.056652    -0.00078018     -0.055872     -0.055872
    30-Jun-1925    -0.0069909     -0.0010415    -0.0059494    -0.0059494
    30-Sep-1925     0.0052352     -0.0011402     0.0063755     0.0063755
    31-Dec-1925      0.036713     0.00070754      0.036006      0.036006

TQTT and CQTT are 220-by-4 timetables containing the trend and cyclical components, respectively, of the series in TTQ. Variables in the input and output timetables correspond.

By default, hpfilter filters all variables in the input table or timetable. To select a subset of variables, set the DataVariables option.

To compare outputs between different tabular inputs, apply the Hodrick-Prescott filter to all variables in the table of monthly data DataTableMth and the timetable of monthly data TTM.

% Table input of daily data
DTM = rmmissing(DataTableMth);
[TMDT,CMDT] = hpfilter(DTM);
size(TMDT)

ans = 1×2

   656     4

tail(TMDT)

                Return      DivYld      CapGain     CapGainA
               ________    _________    ________    ________

    May1925     0.02665    0.0045709    0.022079    0.022079
    Jun1925      0.0275     0.004558    0.022942    0.022942
    Jul1925    0.028372    0.0045491    0.023823    0.023823
    Aug1925     0.02926    0.0045437    0.024716    0.024716
    Sep1925    0.030152     0.004542     0.02561     0.02561
    Oct1925    0.031049     0.004543    0.026506    0.026506
    Nov1925    0.031941    0.0045461    0.027395    0.027395
    Dec1925    0.032844    0.0045508    0.028293    0.028293

tail(CMDT)

                 Return        DivYld       CapGain     CapGainA 
               __________    __________    _________    _________

    May1925      0.039536    -0.0020878     0.041624     0.041624
    Jun1925      -0.02426    0.00090028     -0.02516     -0.02516
    Jul1925    -0.0095168    0.00066325     -0.01018     -0.01018
    Aug1925      0.018948    -0.0018318      0.02078      0.02078
    Sep1925     -0.013374    0.00076008    -0.014134    -0.014134
    Oct1925      0.037148    9.6588e-05     0.037051     0.037051
    Nov1925     -0.040405    -0.0017316    -0.038674    -0.038674
    Dec1925      0.016747     0.0025421     0.014205     0.014205

% Timetable input of daily data
[TMTT,CMTT] = hpfilter(TTM);
size(TMTT)

ans = 1×2

   656     4

tail(TMTT)

       Time         Return      DivYld      CapGain     CapGainA
    ___________    ________    _________    ________    ________

    01-May-1925     0.02665    0.0045709    0.022079    0.022079
    01-Jun-1925      0.0275     0.004558    0.022942    0.022942
    01-Jul-1925    0.028372    0.0045491    0.023823    0.023823
    01-Aug-1925     0.02926    0.0045437    0.024716    0.024716
    01-Sep-1925    0.030152     0.004542     0.02561     0.02561
    01-Oct-1925    0.031049     0.004543    0.026506    0.026506
    01-Nov-1925    0.031941    0.0045461    0.027395    0.027395
    01-Dec-1925    0.032844    0.0045508    0.028293    0.028293

tail(CMTT)

       Time          Return        DivYld       CapGain     CapGainA 
    ___________    __________    __________    _________    _________

    01-May-1925      0.039536    -0.0020878     0.041624     0.041624
    01-Jun-1925      -0.02426    0.00090028     -0.02516     -0.02516
    01-Jul-1925    -0.0095168    0.00066325     -0.01018     -0.01018
    01-Aug-1925      0.018948    -0.0018318      0.02078      0.02078
    01-Sep-1925     -0.013374    0.00076008    -0.014134    -0.014134
    01-Oct-1925      0.037148    9.6588e-05     0.037051     0.037051
    01-Nov-1925     -0.040405    -0.0017316    -0.038674    -0.038674
    01-Dec-1925      0.016747     0.0025421     0.014205     0.014205

Because the data is disaggregated, the outputs of the daily data have more rows than from the quarterly data. The filter results of the daily inputs are equal among the corresponding outputs, but hpfilter returns tables of results, instead of timetables, when you supply data in a table.

Visually Compare Results from Various Smoothing Parameter Values

Since R2022a

Load the Nelson-Plosser macroeconomic data set Data_NelsonPlosser.mat, which contains series measured yearly in the table DataTable.

load Data_NelsonPlosser

Filter the real and nominal GNP series, GNPR and GNPN, respectively. Plot the trend component with each series by additionally returning the vector of graphics objects. Set the smoothing parameter to 100, as suggested in [1] for yearly data.

[TTblHP,CTblHP,hHP] = hpfilter(DataTimeTable,Smoothing=100, ...
    DataVariables=["GNPR" "GNPN"]);

Filter the series again, but set the smoothing parameter to 6.25, which is the suggested smoothing parameter value in [3] for yearly data.

figure
[TTblRU,CTblRU,hRU] = hpfilter(DataTimeTable,Smoothing=6.25, ...
    DataVariables=["GNPR" "GNPN"]);

The smoothed trend of the latter plot contains more higher frequency cycles than the former plot, and, therefore, the smoothed trend in the latter plot follows the data more tightly.

Experiment with the smoothing parameter value by filtering the series several more times and setting the smoothing parameter to 0, 10, 100, 1000, 10,000, and Inf. Plot each set of results by not returning any outputs.

smoothing = [10.^(0:4) Inf];
tiledlayout(2,3)
for j = 1:numel(smoothing)
    nexttile
    hpfilter(DataTimeTable,Smoothing=smoothing(j), ...
        DataVariables=["GNPR" "GNPN"]);
    title("\lambda = " + string(smoothing(j)));
    legend("off")
end

Input Arguments

Y — Time series data

numeric matrix

Time series data, specified as a numObs-by-numVars numeric matrix. Each column of Y corresponds to a variable, and each row corresponds to an observation.

Data Types: double

Tbl — Time series data

table | timetable

Since R2022a

Time series data, specified as a table or timetable with numObs rows. Each row of Tbl is an observation.

Specify numVars variables to filter by using the DataVariables argument. The selected variables must be numeric.

ax — Axes on which to plot

Axes object

Since R2022a

Axes on which to plot, specified as an Axes object.

By default, hpfilter plots to the current axes (gca).

Note

hpfilter removes, from the specified data, all rows containing at least one missing observation, represented by a NaN value. (since R2022a)

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: hpfilter(Tbl,Smoothing=100,DataVariables=1:5) applies the Hodrick-Prescott filter to the first five variables in the input table Tbl and sets the smoothing parameter to 100.

Smoothing — Trend component smoothing parameter

1600 (default) | Inf | nonnegative numeric scalar | nonnegative numeric vector

Since R2022a

Trend component smoothing parameter, specified as a nonnegative numeric scalar or vector of length numVars.

For a scalar, hpfilter applies Smoothing to all specified input series. For a vector, hpfilter applies Smoothing(k) to specified input series k in the data.

If Smoothing(k) = 0, hpfilter does not smooth the corresponding trend components. In this case, these conditions apply:

• Trend(:,k) = y_k, where y_k is the input data of specified variable k.

• Cyclical(:,k) = zeros(numObs,1).

If Smoothing(k) = Inf, hpfilter applies maximum smoothing. In this case, these conditions apply:

• Trend(:,k) is the linear time trend computed by least squares.

• Cyclical(:,k) is the detrended series.

As the smoothing parameter increases, Trend approaches the linear time trend.

The default is 1600, which is suggested in [1] and [3] for quarterly data.

Example: Smoothing=100

Data Types: double

FilterType — Type of filter

"two-sided" (default) | "one-sided" | character vector

Since R2023a

Type of filter, specified as value in this table.

Value	Description
"two-sided"	hpfilter implements the two-sided Hodrick-Prescott filter [1].
"one-sided"	hpfilter implements the one-sided Hodrick-Prescott filter [4].

Example: FilterType="one-sided"n

Data Types: char | string

DataVariables — Variables in Tbl

all variables (default) | string vector | cell vector of character vectors | vector of integers | logical vector

Since R2022a

Variables in Tbl that hpfilter filters, specified as a string vector or cell vector of character vectors containing variable names in Tbl.Properties.VariableNames, or an integer or logical vector representing the indices of names. The selected variables must be numeric.

Example: DataVariables=["GDP" "CPI"]

Example: DataVariables=[true true false false] or DataVariables=[1 2] selects the first and second table variables.

Data Types: double | logical | char | cell | string

Output Arguments

Trend — Smoothed trend component τ_t

numeric vector | numeric matrix

Trend component τ_t of each series in the data, returned as a numObs-by-numVars numeric matrix. hpfilter returns Trend when you supply the input Y.

Cyclical — Cyclical component c_t

numeric vector | numeric matrix

Cyclical component c_t of each series in the data, returned as a numObs-by-numVars numeric matrix. hpfilter returns Cyclical when you supply the input Y.

TTbl — Smoothed trend component τ_t

table | timetable

Since R2022a

Trend component τ_t of each specified series, returned as a numObs-by-numVars table or timetable, the same data type as Tbl. hpfilter returns TTbl when you supply the input Tbl.

CTbl — Cyclical component c_t

table | timetable

Since R2022a

Cyclical component c_t of each specified series, returned as a numObs-by-numVars table or timetable, the same data type as Tbl. hpfilter returns CTbl when you supply the input Tbl.

h — Handles to plotted graphics objects

vector of graphics objects

Since R2022a

Handles to plotted graphics objects, returned as a vector of graphics objects. hpfilter plots the data and trend only when you return no outputs or you return h.

h contains unique plot identifiers, which you can use to query or modify properties of the plot.

More About

Hodrick-Prescott Filter

The Hodrick-Prescott filter decomposes an observed time series y_t (Y) into a trend component τ_t (Trend) and a cyclical component c_t (Cyclical) such that y_t = τ_t + c_t. The method implements a high-pass filter for the cycle that penalizes variations in the trend to a degree determined by the smoothing parameter [1].

The objective function of the filter is

$$f({\tau }_t)={\displaystyle \sum _{t=1}^T{\left(y_t-{\tau }_t\right)}^2}+\lambda {\displaystyle \sum _{t=2}^{T-1}{\left[\left({\tau }_{t+1}-{\tau }_t\right)-\left({\tau }_t-{\tau }_{t-1}\right)\right]}^2},$$

where:

• T is the sample size.

• λ is the smoothing parameter (smoothing).

• y_t – τ_t = c_t.

The programming problem is to minimize the objective function over τ₁,…,τ_T. The objective penalizes the sum of squares for the cyclical component with the sum of squares of second-order differences for the trend component (trend acceleration penalty). If λ = 0, the minimum of the objective is 0 with τ_t = y_t for all t. As λ increases, the penalty for a flexible trend increases, resulting in an increasingly smoother trend. When λ is arbitrarily large, the trend acceleration approaches 0, resulting in a linear trend.

This figure shows the effects of increasing the smoothing parameter on the trend component for a simulated series.

The filter is equivalent to a cubic spline smoother, where the smoothed component is τ_t.

Tips

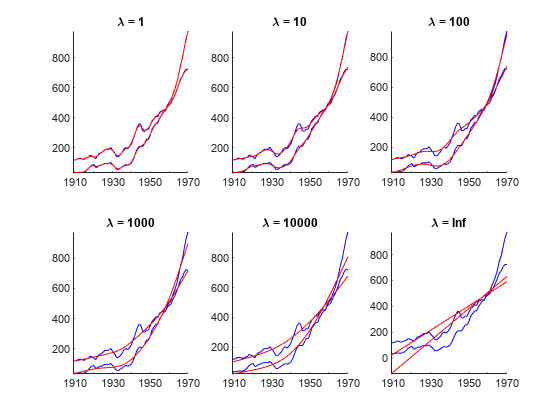
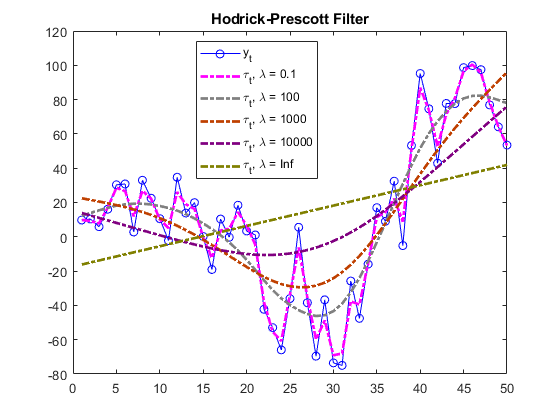
• Hodrick and Prescott [1] suggest values for the smoothing parameter λ (Smoothing) that depend upon the periodicity of the data, and Ravn and Uhlig [3] suggest adjustments to those values. This table contains their suggested smoothing parameter values for several data periodicities.

  Periodicity	Hodrick and Prescott Suggested Smoothing	Ravn and Uhlig Suggested Smoothing
  Yearly	100	6.25
  Quarterly	1600	1600
  Monthly	14400	129600

• Supply a vector of smoothing parameters for the Smoothing name-value argument to test alternatives. Plot the results to visually compare the alternatives.

• The default two-sided filter (see FilterType) uses future values of the input series to compute outputs at time t. Because the filter is typically applied to historical data, the results can contain anomalous end effects unsuitable for forecasting [4]. The one-sided filter, by contrast, is causal because it uses only current and previous values of the input series. As a result, the one-sided filter does not revise outputs when new data becomes available.

Algorithms

hpfilter implements the closed-form solution in [2], Appendix A to the original Hodrick-Prescott programming problem [1]. Therefore, hpfilter requires complete data and removes NaN values in the input data by using listwise deletion.

References

[1] Hodrick, Robert J., and Edward C. Prescott. "Postwar U.S. Business Cycles: An Empirical Investigation." Journal of Money, Credit and Banking 29, no. 1 (February 1997): 1–16. https://doi.org/10.2307/2953682.

[2] Hodrick, Robert J. "An Exploration of Trend-Cycle Decomposition Methodologies in Simulated Data." National Bureau of Economic Research Working Paper No. w26750. Social Science Research Network (February 2020). https://papers.ssrn.com/abstract=3539317.

[3] Ravn, Morton O., and Harald Uhlig. "On Adjusting the Hodrick-Prescott Filter for the Frequency of Observations." The Review of Economics and Statistics 84 , no. 2 (May 2002): 371–76. https://doi.org/10.1162/003465302317411604.

[4] Stock, James H., and Mark W. Watson. "Forecasting Inflation." Journal of Monetary Economics 44, no. 2 (October 1999): 293–335. https://doi.org/10.1016/S0304-3932(99)00027-6.

Version History

Introduced in R2006b

R2024b: Optional positional input is removed and issues error

When you use the optional positional input of hpfilter to specify the smoothing parameter value, MATLAB^® issues an error stating that the syntax is removed. To avoid the error, replace the optional positional input by using the Name=Value syntax.

This syntax issues an error.

hpfilter(Data,smoothing)

This syntax is its replacement.

hpfilter(Data,Smoothing=smoothing)

R2024a: Optional positional input is being removed and issues warning

When you use the optional positional input of hpfilter to specify the smoothing parameter value, MATLAB issues a warning stating that the syntax will be removed. To avoid the warning, replace the optional positional input by using the Name=Value syntax.

This syntax issues a warning.

hpfilter(Data,smoothing)

This syntax is its replacement.

hpfilter(Data,Smoothing=smoothing)

R2023b: Optional positional input is being removed

The optional positional input of hpfilter that specifies the smoothing parameter value will be removed. To replace the optional positional input, use the Name=Value syntax.

This syntax specifies an optional positional input and is being removed.

hpfilter(Data,smoothing)

This syntax is its replacement.

hpfilter(Data,Smoothing=smoothing)

R2023a: Apply one-sided Hodrick-Prescott filter to time series

The hpfilter function implements the one-sided Hodrick-Prescott filter. Whereas the default two-sided filter uses the entire input time series to filter each observation y_t, the one-sided filter uses only the previous and current observations to filter each y_t.

To specify the one-sided Hodrick-Prescott filter, set the FilterType optional name-value argument to "one-sided".

R2022a: hpfilter accepts input data in tables and timetables, and returns results in tables

In addition to accepting input data in numeric arrays, hpfilter accepts input data in tables and timetables. When you supply data in a table or timetable, the following conditions apply:

• hpfilter chooses the default series on which to operate, but you can use the DataVariables name-value argument to select variables.

• hpfilter returns results and selected options in tables or timetables.

R2022a: hpfilter supports name-value argument syntax for optional input

Instead of using the optional positional input of hpfilter that specifies the smoothing value, use the Name=Value argument syntax.

This syntax specifies the optional positional input before R2022a.

hpfilter(Data,smoothing)

smoothing is the value of the smoothing parameter.

This syntax is the recommended syntax for R2022a and later releases.

hpfilter(Data,Smoothing=smoothing)

R2022a: hpfilter removes missing values from the data

hpfilter removes missing observations, specified by NaN values, from the data by using listwise deletion. That is, if a row of the input data contains one NaN value, the function removes the entire row.

In previous releases, hpfilter issued an error when at least one observation was missing.