hfilter

Hamilton filter for trend and cyclical components

Since R2023a

Syntax

[Trend,Cyclical] = hfilter(Y)

[TTbl,CTbl] = hfilter(Tbl)

[___] = hfilter(___,Name=Value)

hfilter(___)

hfilter(ax,___)

[___,h] = hfilter(___)

Description

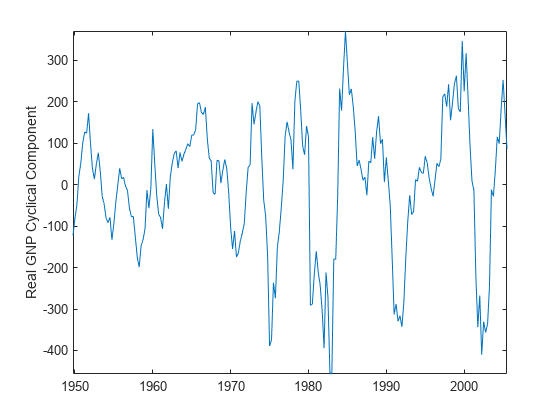
The hfilter function applies the Hamilton filter to separate one or more time series into additive trend and cyclical components. hfilter optionally plots the series and trend component, with cycles removed.

In addition to the Hamilton filter, Econometrics Toolbox™ supports the Baxter-King (bkfilter), Christiano-Fitzgerald (cffilter), and Hodrick-Prescott (hpfilter) filters.

[Trend,Cyclical] = hfilter(Y) returns the additive trend and cyclical components from applying the Hamilton filter [2] to each variable (column) of an input matrix of time series data.

[TTbl,CTbl] = hfilter(Tbl) returns tables or timetables containing variables for the trend and cyclical components from applying the Hamilton filter to each variable in an input table or timetable. To select different variables to filter, use the DataVariables name-value argument.

[___] = hfilter(___,Name=Value) specifies options using one or more name-value arguments in addition to any of the input argument combinations in previous syntaxes. hfilter returns the output argument combination for the corresponding input arguments. For example, hfilter(Tbl,LeadLength=4,DataVariables=1:5) applies the Hamilton filter to the first five variables in the input table Tbl, and, for each selected variable, specifies the lead y_{t + 4} as the response variable in the filter weight regression.

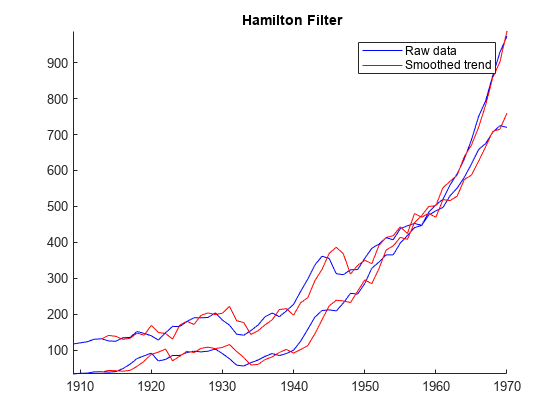
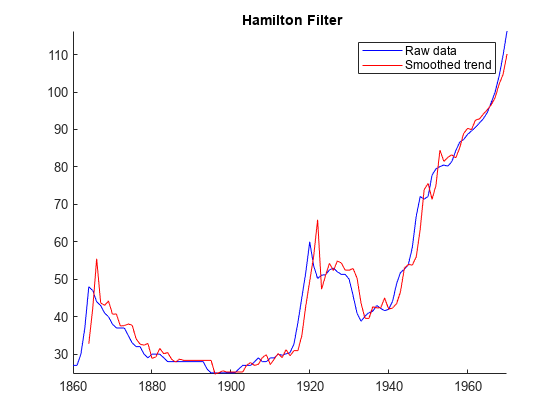
hfilter(___) plots time series variables in the input data and their respective smoothed trend components (cycles removed), computed by the Hamilton filter, on the same axes.

hfilter(ax,___) plots on the axes specified by ax instead of the current axes (gca). ax can precede any of the input argument combinations in the previous syntaxes.

[___,h] = hfilter(___) plots the specified series and their trend components, and additionally returns handles to plotted graphics objects. Use elements of h to modify properties of the plot after you create it.

Examples

Apply Hamilton Filter to Matrix of Data

Plot the cyclical component of the US post-WWII, seasonally adjusted, quarterly, real gross national product (GNPR).

load Data_GNP
GNPR = Data(:,2);
[trend,cyclical] = hfilter(GNPR);
T = numel(trend)

T = 
235

trend and cyclical are 235-by-1 vectors containing the trend and cyclical components, respectively, resulting from applying the Hamilton filter to the series with default lead and lag lengths. The first 7 values are NaNs.

plot(dates,cyclical) 
axis tight
ylabel("Real GNP Cyclical Component")

Apply Hamilton Filter to Table Variables

Apply the Hamilton filter to all variables in input table variables.

Load the Schwert stock data set Data_SchwertStock.mat, which contains monthly returns of the NYSE index from 1871 through 2008 in DataTimeTableMth, among three other variables (for details, enter Description). Remove all missing observations from all series.

load Data_SchwertStock
TTM = rmmissing(DataTimeTableMth);

Aggregate the monthly data in the timetable to quarterly measurements.

TTQ = convert2quarterly(TTM);

Apply the Hamilton filter to all variables in the quarterly timetable. Use the default lead and lag lengths.

[TQTT,CQTT] = hfilter(TTQ);
size(TQTT)

ans = 1×2

   220     4

TQTT and CQTT are 220-by-4 timetables containing the trend and cyclical components, respectively, of the series in TTQ. Variables in the input and output timetables correspond. By default, hfilter filters all variables in the input table or timetable. To select a subset of variables, set the DataVariables option.

The default lead and lag lengths are 4. Consequently, the first 7 rows in the output timetable are NaN-valued.

Remove the leading and lagging NaNs from the trends and display what remains.

TQTTCut = rmmissing(TQTT);
CQTTCut = rmmissing(CQTT);
TQTTCut

TQTTCut=209×4 timetable
       Time          Return       DivYld        CapGain       CapGainA  
    ___________    __________    _________    ___________    ___________

    31-Dec-1873     0.0052994    0.0037312    -0.00091529     0.00032353
    31-Mar-1874     0.0028083     0.003099     -0.0024575     -0.0018408
    30-Jun-1874     0.0028806    0.0041575     -0.0027131     -0.0019406
    30-Sep-1874     0.0033883    0.0030027     -0.0018109     -0.0014369
    31-Dec-1874     0.0053945    0.0032678     8.5274e-05     0.00027652
    31-Mar-1875     0.0051083    0.0026911      0.0007776     0.00072217
    30-Jun-1875     0.0035854    0.0032398    -0.00070225    -0.00041718
    30-Sep-1875     0.0081389    0.0037002      0.0032879      0.0045539
    31-Dec-1875     0.0052623    0.0029082     0.00081654     0.00098183
    31-Mar-1876     0.0074993    0.0033872      0.0030136      0.0029454
    30-Jun-1876    -0.0024581    0.0033423     -0.0052757     -0.0060788
    30-Sep-1876      0.006896    0.0022414    -0.00079166     0.00056363
    31-Dec-1876     0.0041519    0.0043172     0.00012738    -8.1701e-06
    31-Mar-1877     0.0035486    0.0025065     -0.0013859      -0.001144
    30-Jun-1877     0.0049609    0.0041852     0.00028714     0.00045375
    30-Sep-1877     0.0043711    0.0038399     0.00039172     0.00027915
      ⋮

CQTTCut

CQTTCut=209×4 timetable
       Time          Return        DivYld         CapGain       CapGainA 
    ___________    __________    ___________    ___________    __________

    31-Dec-1873       0.12276     -0.0018286         0.0963       0.12583
    31-Mar-1874      -0.02564     -0.0010152      -0.010496     -0.023075
    30-Jun-1874    3.9596e-05     -0.0010583      -0.002827     0.0017616
    30-Sep-1874      0.016762     -0.0027748       0.018478      0.021359
    31-Dec-1874    -0.0067498       0.001779     -0.0028101    -0.0066786
    31-Mar-1875      0.012784     0.00012197       0.010181      0.014357
    30-Jun-1875     -0.011816     0.00066183       -0.02152     -0.011715
    30-Sep-1875     -0.020076    -4.8708e-05      -0.014556     -0.020143
    31-Dec-1875    -0.0097873    -0.00063718    -0.00081654    -0.0077777
    31-Mar-1876     -0.011327     -0.0013573     -0.0057609    -0.0088029
    30-Jun-1876     0.0094729      0.0010775    -0.00067668     0.0086738
    30-Sep-1876     -0.061711      0.0034416      -0.059335     -0.061062
    31-Dec-1876     0.0017068      0.0025794     -0.0070239    -0.0010298
    31-Mar-1877     -0.040981        0.00309      -0.050659     -0.041885
    30-Jun-1877      -0.09557      0.0024379      -0.072017     -0.097686
    30-Sep-1877      0.059143      0.0020562       0.060833      0.057339
      ⋮

To compare outputs between different tabular inputs, apply the Hamilton filter to all variables in the table of monthly data DataTableMth and the timetable of monthly data TTM.

% Table input of daily data
DTM = rmmissing(DataTableMth);
[TMDT,CMDT] = hfilter(DTM);
TMDT = rmmissing(TMDT);
CMDT = rmmissing(CMDT);
size(TMDT)

ans = 1×2

   645     4

tail(TMDT)

                Return       DivYld       CapGain       CapGainA 
               _________    _________    __________    __________

    May1925    0.0076851    0.0035499     0.0033316     0.0032399
    Jun1925     0.007946    0.0055856     0.0038195     0.0037338
    Jul1925     0.010239    0.0044464     0.0063502     0.0063067
    Aug1925    0.0080799    0.0035821      0.003389     0.0037078
    Sep1925    0.0076608    0.0055354     0.0037118      0.003575
    Oct1925    0.0081879     0.004496     0.0042474     0.0041497
    Nov1925     0.005312    0.0034493    0.00060642    0.00071388
    Dec1925     0.009001    0.0049537     0.0052133     0.0048893

tail(CMDT)

                 Return        DivYld        CapGain       CapGainA 
               __________    ___________    __________    __________

    May1925      0.058501     -0.0010668      0.060371      0.060463
    Jun1925    -0.0047057    -0.00012725    -0.0060375    -0.0059518
    Jul1925     0.0086164     0.00076594     0.0072928     0.0073363
    Aug1925      0.040128    -0.00087019      0.042107      0.041788
    Sep1925     0.0091173    -0.00023334     0.0077642      0.007901
    Oct1925      0.060009     0.00014365       0.05931      0.059407
    Nov1925     -0.013777    -0.00063483     -0.011885     -0.011993
    Dec1925       0.04059      0.0021392      0.037285      0.037609

% Timetable input of daily data
[TMTT,CMTT] = hfilter(TTM);
TMTT = rmmissing(TMTT);
CMTT = rmmissing(CMTT);
size(TMTT)

ans = 1×2

   645     4

tail(TMTT)

       Time         Return       DivYld       CapGain       CapGainA 
    ___________    _________    _________    __________    __________

    01-May-1925    0.0076851    0.0035499     0.0033316     0.0032399
    01-Jun-1925     0.007946    0.0055856     0.0038195     0.0037338
    01-Jul-1925     0.010239    0.0044464     0.0063502     0.0063067
    01-Aug-1925    0.0080799    0.0035821      0.003389     0.0037078
    01-Sep-1925    0.0076608    0.0055354     0.0037118      0.003575
    01-Oct-1925    0.0081879     0.004496     0.0042474     0.0041497
    01-Nov-1925     0.005312    0.0034493    0.00060642    0.00071388
    01-Dec-1925     0.009001    0.0049537     0.0052133     0.0048893

tail(CMTT)

       Time          Return        DivYld        CapGain       CapGainA 
    ___________    __________    ___________    __________    __________

    01-May-1925      0.058501     -0.0010668      0.060371      0.060463
    01-Jun-1925    -0.0047057    -0.00012725    -0.0060375    -0.0059518
    01-Jul-1925     0.0086164     0.00076594     0.0072928     0.0073363
    01-Aug-1925      0.040128    -0.00087019      0.042107      0.041788
    01-Sep-1925     0.0091173    -0.00023334     0.0077642      0.007901
    01-Oct-1925      0.060009     0.00014365       0.05931      0.059407
    01-Nov-1925     -0.013777    -0.00063483     -0.011885     -0.011993
    01-Dec-1925       0.04059      0.0021392      0.037285      0.037609

Because the data is disaggregated, the outputs of the daily data have more rows than from the quarterly data. The filter results of the daily inputs are equal among the corresponding outputs, but hfilter returns tables of results, instead of timetables, when you supply data in a table.

Set Filter Parameters for Data Periodicity

Load the Nelson-Plosser macroeconomic data set Data_NelsonPlosser.mat, which contains series measured yearly in the timetable DataTimeTable.

load Data_NelsonPlosser

Apply the Hamilton filter to the real and nominal GNP series, GNPR and GNPN, respectively. Set the lead and lag lengths 2 years and 1 year, respectively. Plot the trend component with each series.

hfilter(DataTimeTable,DataVariables=["GNPR" "GNPN"], ...
    LeadLength=2,LagLength=3);

Experiment with filter parameter values by adjusting the interactive controls.

varnames = string(DataTimeTable.Properties.VariableNames);
lead = 2; % LeadLength
lag = 3;  % LagLength
vn = varnames(8); % DataVariables

figure
[TTbl,CTbl,h] = hfilter(DataTimeTable,DataVariables=vn, ...
    LeadLength=lead,LagLength=lag);

Input Arguments

Y — Time series data

numeric matrix

Time series data, specified as a numObs-by-numVars numeric matrix. Each column of Y corresponds to a variable, and each row corresponds to an observation.

Data Types: double

Tbl — Time series data

table | timetable

Time series data, specified as a table or timetable with numObs rows. Each row of Tbl is an observation.

Specify numVars variables to filter by using the DataVariables argument. The selected variables must be numeric.

ax — Axes on which to plot

Axes object

Axes on which to plot, specified as an Axes object.

By default, hfilter plots to the current axes (gca).

Note

hfilter removes, from the specified data, all rows containing at least one missing observation, represented by a NaN value.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: hfilter(Tbl,LeadLength=4,DataVariables=1:5) applies the Hamilton filter to the first five variables in the input table Tbl, and, for each selected variable, specifies the lead y_{t + 4} as the response variable in the filter weight regression.

LeadLength — Filter weight regression response variable lead h

8 (default) | positive integer | vector of positive integers

Filter weight regression response variable lead h, in units of data periodicity, specified as a positive integer or vector of positive integers. That is, the response variable in the regression is y_t+h.

For a scalar, hfilter applies LagLength to all input series.

For a vector, hfilter applies LagLength(j) to series j in the input data.

The default is 8 quarters, suggested in [2].

Example: LeadLength=[4 8] specifies that the response variable of the filter weight regression for the first series in the input data is y_t+4 and the response variable for the second input series is y_t+8.

Data Types: double

LagLength — Number of consecutive lags p

4 (default) | positive integer | vector of positive integers

Number of consecutive lags p of predictor variables y_t, y_t–1, …, y_t+p–1 in the filter weight regression, in units of data periodicity, specified as a positive integer or vector of positive integers. hfilter includes lags 0 through p – 1.

For a scalar, hfilter applies LagLength to all input series.

For a vector, hfilter applies LagLength(j) to series j in the input data.

The default is 4 quarters, suggested in [2].

Example: LagLength=[4 8] specifies lags 0 through 3 as predictors for the regression when filtering the first series of the input data and lags 0 through 8 as predictors for the regression when filtering the second series.

Data Types: double

DataVariables — Variables in Tbl

all variables (default) | string vector | cell vector of character vectors | vector of integers | logical vector

Variables in Tbl that hfilter filters, specified as a string vector or cell vector of character vectors containing variable names in Tbl.Properties.VariableNames, or an integer or logical vector representing the indices of names. The selected variables must be numeric.

Example: DataVariables=["GDP" "CPI"]

Example: DataVariables=[true true false false] or DataVariables=[1 2] selects the first and second table variables.

Data Types: double | logical | char | cell | string

Output Arguments

Trend — Smoothed trend component τ_t

numeric vector | numeric matrix

Smoothed trend component τ_t of each series in the data, returned as a numObs-by-numVars numeric matrix. hfilter returns Trend when you supply the input Y.

The first LeadLength + LagLength – 1 values are NaN.

Cyclical — Cyclical component c_t

table | timetable

Cyclical component c_t of each series in the data, returned as a numObs-by-numVars numeric matrix. hfilter returns Cyclical when you supply the input Y.

The first LeadLength + LagLength – 1 values are NaN.

TTbl — Smoothed trend component τ_t

table | timetable

Smoothed trend component τ_t of each specified series, returned as a numObs-by-numVars table or timetable, the same data type as Tbl. hfilter returns TTbl when you supply the input Tbl.

For each selected series and corresponding LeadLength and LagLength, the first LeadLength + LagLength – 1 values are NaN.

CTbl — Cyclical component c_t

numeric vector | numeric matrix

Cyclical component c_t of each specified series, returned as a numObs-by-numVars table or timetable, the same data type as Tbl. hfilter returns CTbl when you supply the input Tbl.

For each selected series and corresponding LeadLength and LagLength, the first LeadLength + LagLength – 1 values are NaN.

h — Handles to plotted graphics objects

vector of graphics objects

Handles to plotted graphics objects, returned as a vector of graphics objects. hfilter plots the data and trend only when you return no outputs or you return h.

h contains unique plot identifiers, which you can use to query or modify properties of the plot.

More About

Hamilton Filter

The Hamilton filter separates a time series y_t into a trend component τ_t (Trend and TTbl) and cyclical component c_t (Cyclical and CTbl) such that y_t = τ_t + c_t.

The Hamilton filter performs an autoregression of y_t+h on a constant and y_t, y_t–1, …, y_t–p+1, where h is the value of the LeadLength name-value argument and p is the value of the LagLength name-value argument. The filter identifies the trend and cyclical components of y_t at time t + h with the expected value of y_t+h and the forecast error, respectively [2]. The decomposition is based on a definition of business cycle in [1].

Tips

• Regarding a setting for the LeadLength name-value argument, Hamilton [2] states "If we are interested in business cycles, a 2-year horizon should be the standard benchmark." Regarding a setting for the LagLength name-value argument, the article states "One might be tempted to use a richer model to forecast y_t+h, such as using more than 4 lags, or even a nonlinear relation. However, such refinements are completely unnecessary for the goal of extracting a stationary (cyclical) component, and have the significant drawback that the more parameters we try to estimate by regression, the more the small-sample results are likely to differ from the asymptotic predictions."

References

[1] Beveridge, Stephen, and Charles R. Nelson. "A New Approach to Decomposition of Economic Time Series into Permanent and Transitory Components with Particular Attention to Measurement of the 'Business Cycle.'" Journal of Monetary Economics 7 (January 1981): 151–74. https://doi.org/10.1016/0304-3932(81)90040-4.

[2] Hamilton, James D. "Why You Should Never Use the Hodrick-Prescott Filter." The Review of Economics and Statistics 100 (December 2018): 831–43. https://doi.org/10.1162/rest_a_00706.

Version History

Introduced in R2023a