freqrespest
Frequency response estimate via filtering
Syntax
Description
[
computes the frequency response estimate of the input filter System object™. The function estimates by running input data made up from sinusoids with
uniformly distributed random frequencies through the filter and forming the ratio between
output data and input data.h,w] = freqrespest(sysobj)
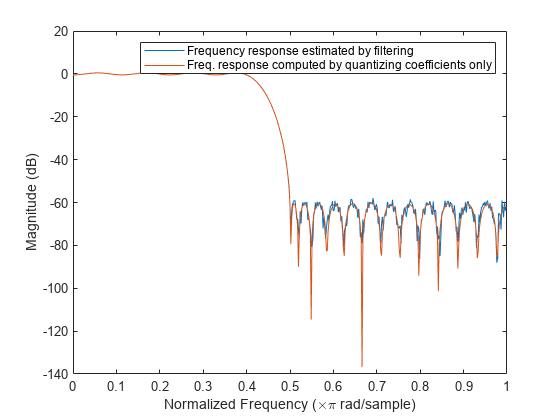
The freqrespest function computes the frequency response estimate
of the input filter object that is close to the frequency response obtained by using only
the quantized coefficients as long as:
No overflow occurs when performing the fixed-point filtering
There isn't significant quantization happening in the fixed-point additions and multiplications
freqrespest can be used as a diagnostic tool for fixed-point
implementations. If freqrespest differs significantly from freqz (which only takes into account the quantization of the coefficients), it
is an indication that at least one of the two conditions might be true.
[
uses the h,w] = freqrespest(sysobj,L,Name=Value)Name-Value pairs as input arguments to specify optional
parameters for the test.
freqrespest( with no
output argument plots the magnitude response estimate of the filter object.sysobj,___)