dsp.NotchPeakFilter
Second-order tunable notching and peaking IIR filter
Description
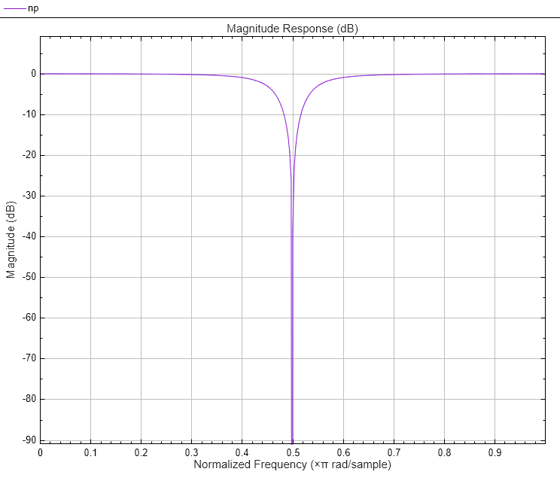
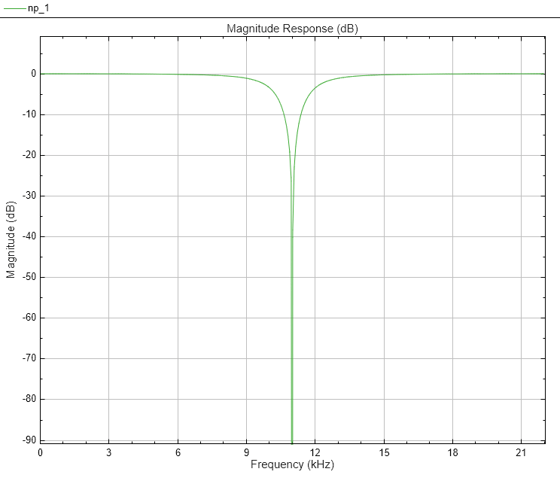
The NotchPeakFilter object filters each channel of the
input using IIR filter implementation. This object implements a second-order notch or peak IIR
filter.
To implement a high-order notch or peak IIR filter,
use the designNotchPeakIIR
function. (since R2023b)
To filter each channel of the input:
Create the
dsp.NotchPeakFilterobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
npFilter = dsp.NotchPeakFilter
npFilter = dsp.NotchPeakFilter(Specification='Quality
factor and center frequency') specifies the quality factor (Q factor) of the
notch or peak filter instead of the 3 dB bandwidth.
npFilter = dsp.NotchPeakFilter(Specification='Coefficients')
specifies the coefficient values that affect bandwidth and center frequency directly,
rather than specifying the design parameters in Hz. This removes the trigonometry
calculations involved when the properties are tuned.
npFilter = dsp.NotchPeakFilter(
returns a notch or peak filter with properties specified by one or more name-value pair
arguments. Unspecified properties have default values.Name=Value)
Properties
Usage
Description
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object™ as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Algorithms
The design equation for the peak filter is:
The design equation for the notch filter is:
with
where ω0 = 2πf0/fs is the center frequency in radians/sample (f0 is the center frequency in Hz and fs is the sampling frequency in Hz). Δω = 2πΔf/fs is the 3 dB bandwidth in radians/sample (Δf is the 3 dB bandwidth in Hz). Note that the two filters are complementary:
The filter is implemented as follows:

where
Notice that Gcf depends only on the center frequency, and G3dB depends only on the 3 dB bandwidth.
References
[1] Orfanidis, Sophocles J. Introduction to Signal Processing. Upper Saddle River, NJ: Prentice-Hall, 1996.
Version History
Introduced in R2014aSee Also
Functions
designNotchPeakIIR|getBandwidth|getCenterFrequency|getOctaveBandwidth|getQualityFactor|tf|outputDelay