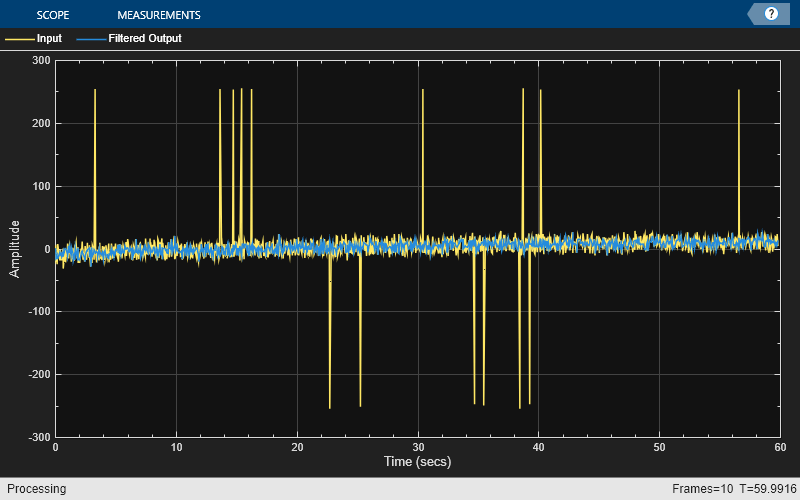
dsp.HampelFilter
Filter outliers using Hampel identifier
Description
The dsp.HampelFilter
System object™ detects and removes the outliers of the input signal by using the Hampel
identifier. The Hampel identifier is a variation of the three-sigma rule of statistics that is
robust against outliers. For each sample of the input signal, the object computes the median
of a window composed of the current sample and adjacent samples on each side of current sample. Len is
the window length you specify through the WindowLength property. The
object also estimates the standard deviation of each sample about its window median by using
the median absolute deviation. If a sample differs from the median by more than the threshold
multiplied by the standard deviation, the filter replaces the sample with the median. For more
information, see Algorithms.
To filter the input signal using a Hampel identifier:
Create the
dsp.HampelFilterobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
hampFilt = dsp.HampelFilterhampFilt, using the default properties.
hampFilt = dsp.HampelFilter(Len)WindowLength property to Len.
hampFilt = dsp.HampelFilter(Len, Lim)WindowLength property to Len and the
Threshold property to Lim.
Example: hampFilt = dsp.HampelFilter(11,2);
hampFilt = dsp.HampelFilter(Name,Value)Name,Value pairs. Unspecified properties
have default values.
Properties
Usage
Description
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
More About
Algorithms

For a given sample of data, xs, the algorithm:
Centers the window of odd length at the current sample.
Computes the local median, mi, and standard deviation, σi, over the current window of data.
Compares the current sample with nσ × σi, where nσ is the threshold value. If , the filter identifies the current sample, xs, as an outlier and replaces it with the median value, mi.
Consider a frame of data that is passed into the Hampel filter.

In this example, the Hampel filter slides a window of length 5 (Len) over the data. The filter has a threshold value of 2 (nσ). To have a complete window at the beginning of the frame, the filter algorithm prepends the frame with Len – 1 zeros. To compute the first sample of the output, the window centers on the sample in the appended frame, the third zero in this case. The filter computes the median, median absolute deviation, and the standard deviation over the data in the local window.

Current sample: xs = 0.
Window of data: win = [0 0 0 0 1].
Local median: mi = median([0 0 0 0 1]) = 0.
Median absolute deviation: . For this window of data, .
Standard deviation: σi = κ × madi = 0, where .
The current sample, xs = 0, does not obey the relation for outlier detection.
Therefore, the Hampel filter outputs the current input sample, xs = 0.
Repeat this procedure for every succeeding sample until the
algorithm centers the window on the sample, marked
as End. Because the window centered on the last samples cannot
be full, these samples are processed with the next frame of input
data.
Here is the first output frame the Hampel filter generates:

The seventh sample of the appended input frame, 23, is an outlier. The Hampel filter replaces this sample with the median over the local window [4 9 23 8 12].
References
[1] Bodenham, Dean. “Adaptive Filtering and Change Detection for Streaming Data.” PH.D. Thesis. Imperial College, London, 2012.
[2] Liu, Hancong, Sirish Shah, and Wei Jiang. “On-line outlier detection and data cleaning.” Computers and Chemical Engineering. Vol. 28, March 2004, pp. 1635–1647.
[3] Suomela, Jukka. Median Filtering Is Equivalent to Sorting, 2014.
Extended Capabilities
Version History
Introduced in R2017a