dsp.FIRInterpolator
Perform polyphase FIR interpolation
Description
The dsp.FIRInterpolator
System object™ performs an efficient polyphase interpolation using an integer upsampling factor
L along the first dimension.
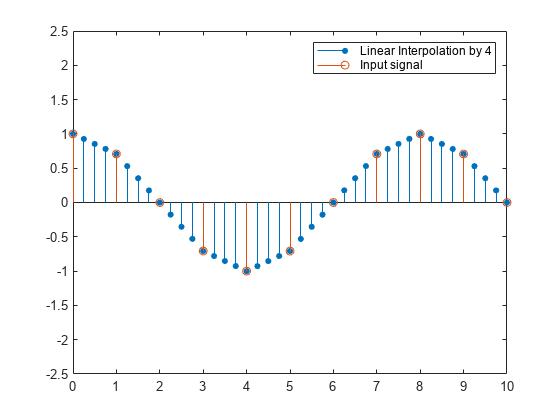
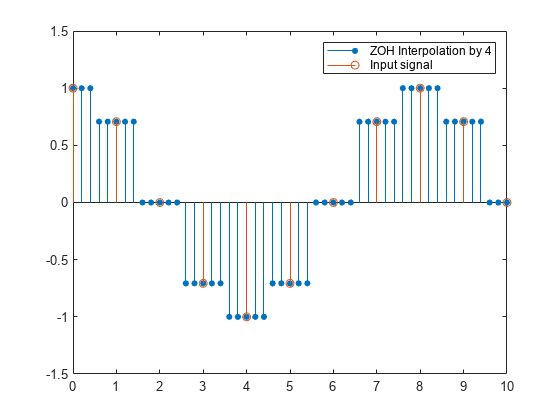
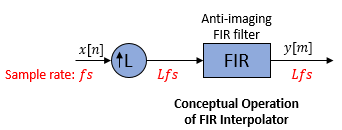
Conceptually, the FIR interpolator (as shown in the schematic) consists of an upsampler
followed by an FIR anti-imaging filter, which is usually an approximation of an ideal
band-limited interpolation filter. The coefficients of the anti-imaging filter can be
specified through the Numerator property, or can be automatically
designed by the object using the designMultirateFIR function.
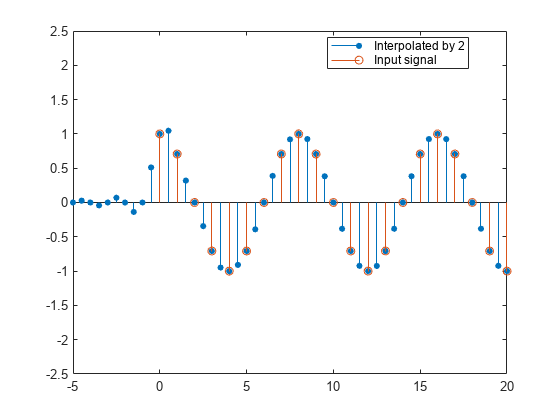
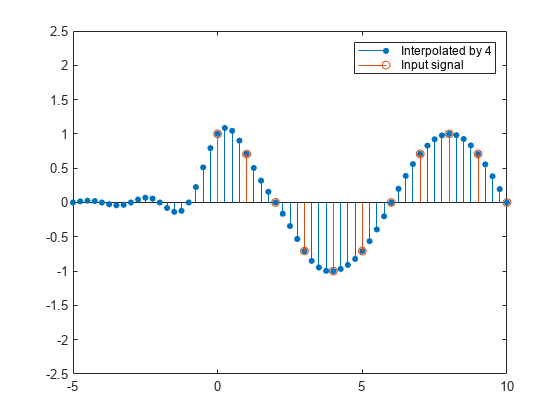
The upsampler upsamples each channel of the input to a higher rate by inserting L–1 zeros between samples. The FIR filter that follows filters each channel of the upsampled data. The resulting discrete-time signal has a sample rate that is L times the original sample rate.
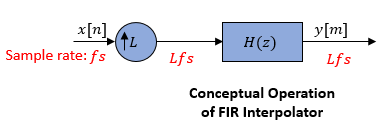
Note that the actual object algorithm implements a direct-form FIR polyphase structure, an efficient equivalent of the combined system depicted in the diagram. For more details, see Algorithms.
To upsample an input:
Create the
dsp.FIRInterpolatorobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
This object supports C/C++ code generation and SIMD code generation under certain conditions. For more information, see Code Generation.
Creation
Syntax
Description
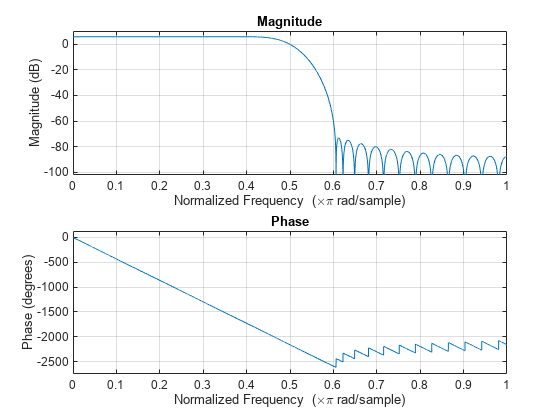
firinterp = dsp.FIRInterpolatordesignMultirateFIR(3,1) function.
firinterp = dsp.FIRInterpolator(L)InterpolationFactor property set to
L. The object designs its filter coefficients
based on the interpolation factor L that you
specify while creating the object using the
designMultirateFIR(L=1) function. The designed
filter corresponds to a lowpass with a cutoff at
π/L in radial frequency units.
firinterp = dsp.FIRInterpolator(L,"Auto")NumeratorSource property set to
"Auto". In this mode, every time there is an
update in the interpolation factor, the object redesigns the filter
using the design method specified in
DesignMethod.
firinterp = dsp.FIRInterpolator(L,num)InterpolationFactor property set to
L and the Numerator
property set to num.
firinterp = dsp.FIRInterpolator(L,method)InterpolationFactor property set to
L and the DesignMethod
property set to method. When you pass the design
method as an input, the NumeratorSource property
is automatically set to "Auto".
firinterp = dsp.FIRInterpolator(___,Name=Value)InterpolationFactor to 6.
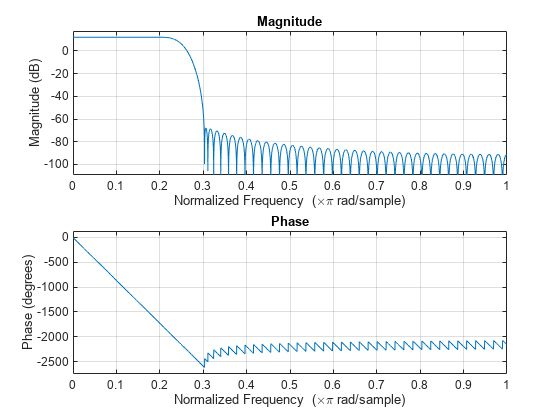
firinterp = dsp.FIRInterpolator(L,"legacy")fir1(15,0.25). The designed filter has a
cutoff frequency of 0.25π radians/sample.
Properties
Usage
Description
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Algorithms
The FIR interpolation filter is implemented efficiently using a polyphase structure.
To derive the polyphase structure, start with the transfer function of the FIR filter:
N+1 is the length of the FIR filter.
You can rearrange this equation as follows:
L is the number of polyphase components, and its value equals the interpolation factor that you specify.
You can write this equation as:
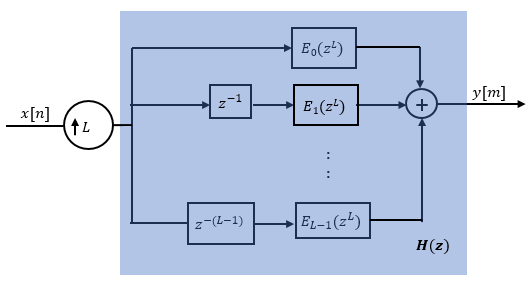
E0(zL), E1(zL), ..., EL-1(zL) are polyphase components of the FIR filter H(z).
Conceptually, the FIR interpolation filter contains an upsampler followed by an FIR lowpass filter H(z).
Replace H(z) with its polyphase representation.
Here is the multirate noble identity for interpolation.
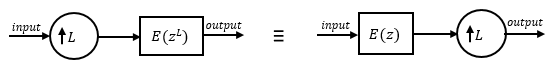
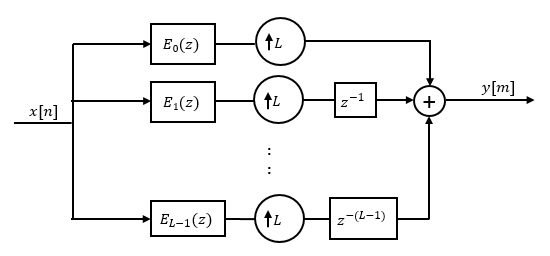
Applying the noble identity for interpolation moves the upsampling operation to after the filtering operation. This move enables you to filter the signal at a lower rate.
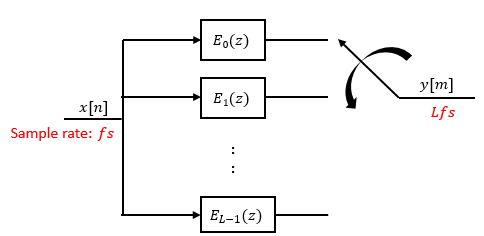
You can replace the upsampling operator, delay block, and adder with a commutator switch. The switch starts on the first branch 0 and moves in the counterclockwise direction, each time receiving one sample from each branch. The interpolator effectively outputs L samples for every one input sample it receives. Hence the sample rate at the output of the FIR interpolation filter is Lfs.
Extended Capabilities
Version History
Introduced in R2012aSee Also
Functions
freqz|freqzmr|filterAnalyzer|info|cost|polyphase|impz|coeffs|outputDelay|designRateConverter