Train Neural Networks with Error Weights
In the default mean squared error performance function (see Train and Apply Multilayer Shallow Neural Networks), each squared error contributes the same amount to the performance function as follows:
However, the toolbox allows you to weight each squared error individually as follows:
The error weighting object needs to have the same dimensions as the target data. In this
way, errors can be weighted according to time step, sample number, signal number or element
number. The following is an example of weighting the errors at the end of a time sequence more
heavily than errors at the beginning of a time sequence. The error weighting object is passed as
the last argument in the call to train.
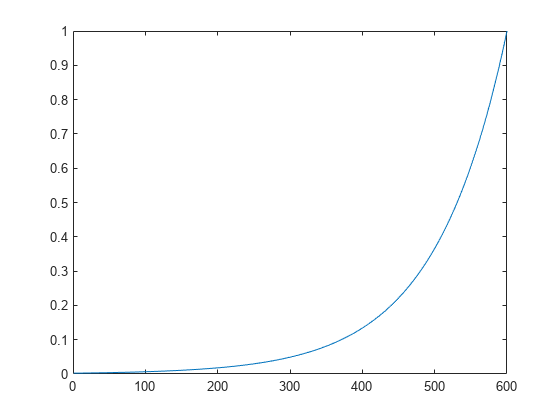
y = laser_dataset; y = y(1:600); ind = 1:600; ew = 0.99.^(600-ind); figure plot(ew)
ew = con2seq(ew);
ftdnn_net = timedelaynet([1:8],10);
ftdnn_net.trainParam.epochs = 1000;
ftdnn_net.divideFcn = '';
[p,Pi,Ai,t,ew1] = preparets(ftdnn_net,y,y,{},ew);
[ftdnn_net1,tr] = train(ftdnn_net,p,t,Pi,Ai,ew1);
The figure illustrates the error weighting for this example. There are 600 time steps in the training data, and the errors are weighted exponentially, with the last squared error having a weight of 1, and the squared error at the first time step having a weighting of 0.0024.
The response of the trained network is shown in the following figure. If you compare this response to the response of the network that was trained without exponential weighting on the squared errors, as shown in Design Time Series Time-Delay Neural Networks, you can see that the errors late in the sequence are smaller than the errors earlier in the sequence. The errors that occurred later are smaller because they contributed more to the weighted performance index than earlier errors.
