Train Variational Autoencoder (VAE) to Generate Images
This example shows how to train a deep learning variational autoencoder (VAE) to generate images.
To generate data that strongly represents observations in a collection of data, you can use a variational autoencoder. An autoencoder is a type of model that is trained to replicate its input by transforming the input to a lower dimensional space (the encoding step) and reconstructing the input from the lower dimensional representation (the decoding step).
This diagram illustrates the basic structure of an autoencoder that reconstructs images of digits.

To generate new images using a variational autoencoder, input random vectors to the decoder.

A variational autoencoder differs from a regular autoencoder in that it imposes a probability distribution on the latent space, and learns the distribution so that the distribution of outputs from the decoder matches that of the observed data. In particular, the latent outputs are randomly sampled from the distribution learned by the encoder.
Load Data
Load the Digits data as in-memory numeric arrays using the digitTrain4DArrayData and digitTest4DArrayData functions. The Digits data set consists of 10,000 synthetic grayscale images of handwritten digits. Each image is 28-by-28 pixels.
XTrain = digitTrain4DArrayData; XTest = digitTest4DArrayData;
Define Network Architecture
Autoencoders have two parts: the encoder and the decoder. The encoder takes an image input and outputs a latent vector representation (the encoding) using a series of downsampling operations such as convolutions. Similarly, the decoder takes as input the latent vector representation, and reconstructs the input using a series of upsampling operations such as transposed convolutions.
To sample the input, the example uses the custom layer samplingLayer. To access this layer, open this example as a live script. The layer takes as input the mean vector concatenated with the log-variance vector and samples elements from . The layer uses the log-variance to make the training process more numerically stable.
Define Encoder Network Architecture
Define the following encoder network that downsamples 28-by-28-by-1 images to 32-by-1 latent vectors.

For image input, specify an image input layer with input size matching the training data. Do not normalize the data.
To downsample the input, specify two blocks of 2-D convolution and ReLU layers.
To output a concatenated vector of means and log-variances, specify a fully connected layer with twice the number of output channels as the number of latent channels.
To sample an encoding specified by the statistics, include a sampling layer using the custom layer
samplingLayer. To access this layer, open this example as a live script.
numLatentChannels = 32;
imageSize = [28 28 1];
layersE = [
imageInputLayer(imageSize,Normalization="none")
convolution2dLayer(3,32,Padding="same",Stride=2)
reluLayer
convolution2dLayer(3,64,Padding="same",Stride=2)
reluLayer
fullyConnectedLayer(2*numLatentChannels)
samplingLayer];Define Decoder Network Architecture
Define the following decoder network that reconstructs 28-by-28-by-1 images from 32-by-1 latent vectors.

For feature vector input, specify a feature input layer with input size matching the number of latent channels.
Project and reshape the latent input to 7-by-7-by-64 arrays using the custom layer
projectAndReshapeLayer, attached to this example as a supporting file. To access this layer, open the example as a live script. Specify a projection size of[7 7 64].To upsample the input, specify two blocks of transposed convolution and ReLU layers.
To output an image of size 28-by-28-by-1, include a transposed convolution layer with one 3-by-3 filter.
To map the output to values in the range [0,1], include a sigmoid activation layer.
projectionSize = [7 7 64];
numInputChannels = imageSize(3);
layersD = [
featureInputLayer(numLatentChannels)
projectAndReshapeLayer(projectionSize)
transposedConv2dLayer(3,64,Cropping="same",Stride=2)
reluLayer
transposedConv2dLayer(3,32,Cropping="same",Stride=2)
reluLayer
transposedConv2dLayer(3,numInputChannels,Cropping="same")
sigmoidLayer];To train both networks with a custom training loop and enable automatic differentiation, convert the layer arrays to dlnetwork objects.
netE = dlnetwork(layersE); netD = dlnetwork(layersD);
Define Model Loss Function
Define a function that returns the model loss and the gradients of the loss with respect to the learnable parameters.
The modelLoss function, defined in the Model Loss Function section of the example, takes as input the encoder and decoder networks and a mini-batch of input data, and returns the loss and the gradients of the loss with respect to the learnable parameters in the networks. To compute the loss, the function uses the ELBOloss function, defined in the ELBO Loss Function section of the example, takes as input the mean and log-variances output by the encoder and uses them to compute the evidence lower bound (ELBO) loss.
Specify Training Options
Train for 150 epochs with a mini-batch size of 128 and a learning rate of 0.001.
numEpochs = 150; miniBatchSize = 128; learnRate = 1e-3;
Train Model
Train the model using a custom training loop.
Create a minibatchqueue object that processes and manages mini-batches of images during training. For each mini-batch:
Convert the training data to an array datastore. Specify to iterate over the 4th dimension.
Use the custom mini-batch preprocessing function
preprocessMiniBatch(defined at the end of this example) to concatenate multiple observations into a single mini-batch.Format the image data with the dimension labels
"SSCB"(spatial, spatial, channel, batch). By default, theminibatchqueueobject converts the data todlarrayobjects with underlying typesingle.Train on a GPU if one is available. By default, the
minibatchqueueobject converts each output to agpuArrayif a GPU is available. Using a GPU requires Parallel Computing Toolbox™ and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox).To ensure all mini-batches are the same size, discard any partial mini-batches.
dsTrain = arrayDatastore(XTrain,IterationDimension=4); numOutputs = 1; mbq = minibatchqueue(dsTrain,numOutputs, ... MiniBatchSize = miniBatchSize, ... MiniBatchFcn=@preprocessMiniBatch, ... MiniBatchFormat="SSCB", ... PartialMiniBatch="discard");
Initialize the parameters for the Adam solver.
trailingAvgE = []; trailingAvgSqE = []; trailingAvgD = []; trailingAvgSqD = [];
Calculate the total number of iterations for the training progress monitor
numObservationsTrain = size(XTrain,4); numIterationsPerEpoch = ceil(numObservationsTrain / miniBatchSize); numIterations = numEpochs * numIterationsPerEpoch;
Initialize the training progress monitor. Because the timer starts when you create the monitor object, make sure that you create the object close to the training loop.
monitor = trainingProgressMonitor( ... Metrics="Loss", ... Info="Epoch", ... XLabel="Iteration");
Train the network using a custom training loop. For each epoch, shuffle the data and loop over mini-batches of data. For each mini-batch:
Evaluate the model loss and gradients using the
dlfevalandmodelLossfunctions.Update the encoder and decoder network parameters using the
adamupdatefunction.Display the training progress.
epoch = 0; iteration = 0; % Loop over epochs. while epoch < numEpochs && ~monitor.Stop epoch = epoch + 1; % Shuffle data. shuffle(mbq); % Loop over mini-batches. while hasdata(mbq) && ~monitor.Stop iteration = iteration + 1; % Read mini-batch of data. X = next(mbq); % Evaluate loss and gradients. [loss,gradientsE,gradientsD] = dlfeval(@modelLoss,netE,netD,X); % Update learnable parameters. [netE,trailingAvgE,trailingAvgSqE] = adamupdate(netE, ... gradientsE,trailingAvgE,trailingAvgSqE,iteration,learnRate); [netD, trailingAvgD, trailingAvgSqD] = adamupdate(netD, ... gradientsD,trailingAvgD,trailingAvgSqD,iteration,learnRate); % Update the training progress monitor. recordMetrics(monitor,iteration,Loss=loss); updateInfo(monitor,Epoch=epoch + " of " + numEpochs); monitor.Progress = 100*iteration/numIterations; end end

Test Network
Test the trained autoencoder with a the held-out test set. Create a mini-batch queue of the data using the same steps as for the training data, except do not discard any partial mini-batches of data.
dsTest = arrayDatastore(XTest,IterationDimension=4); numOutputs = 1; mbqTest = minibatchqueue(dsTest,numOutputs, ... MiniBatchSize = miniBatchSize, ... MiniBatchFcn=@preprocessMiniBatch, ... MiniBatchFormat="SSCB");
Make predictions using the trained autoencoder using the modelPredictions function.
YTest = modelPredictions(netE,netD,mbqTest);
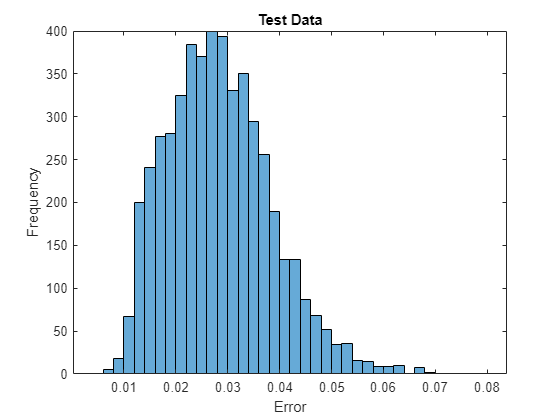
Visualize the reconstruction errors by taking the mean-squared-error of the test images and the reconstructed images and visualizing them in a histogram.
err = mean((XTest-YTest).^2,[1 2 3]); figure histogram(err) xlabel("Error") ylabel("Frequency") title("Test Data")
Generate New Images
Generate a batch of new images by passing randomly sampled image encodings through the decoder.
numImages = 64;
ZNew = randn(numLatentChannels,numImages);
ZNew = dlarray(ZNew,"CB");
YNew = predict(netD,ZNew);
YNew = extractdata(YNew);Display the generated images in a figure.
figure
I = imtile(YNew);
imshow(I)
title("Generated Images")
Here, the VAE has learned a strong feature representation that allows it to generate images that are similar to the training data.
Helper Functions
Model Loss Function
The modelLoss function takes as input the encoder and decoder networks and a mini-batch of input data, and returns the loss and the gradients of the loss with respect to the learnable parameters in the networks. The function passes the training images through the encoder and passes the resulting image encodings through the decoder. To calculate the loss, the function uses the elboLoss function with the mean and log-variance statistics output by the sampling layer of the encoder.
function [loss,gradientsE,gradientsD] = modelLoss(netE,netD,X) % Forward through encoder. [Z,mu,logSigmaSq] = forward(netE,X); % Forward through decoder. Y = forward(netD,Z); % Calculate loss and gradients. loss = elboLoss(Y,X,mu,logSigmaSq); [gradientsE,gradientsD] = dlgradient(loss,netE.Learnables,netD.Learnables); end
ELBO Loss Function
The ELBOloss function takes the mean and log-variances output by the encoder and uses them to compute the evidence lower bound (ELBO) loss. The ELBO loss is given by the sum of two separate loss terms:
.
The reconstruction loss measures how close the decoder output is to the original input by using the mean-squared error (MSE):
.
The KL loss, or Kullback–Leibler divergence, measures the difference between two probability distributions. Minimizing the KL loss in this case means ensuring that the learned means and variances are as close as possible to those of the target (normal) distribution. For a latent dimension of size , the KL loss is obtained as
.
The practical effect of including a KL loss term is to pack the clusters learned due to the reconstruction loss tightly around the center of the latent space, forming a continuous space to sample from.
function loss = elboLoss(Y,T,mu,logSigmaSq) % Reconstruction loss. reconstructionLoss = mse(Y,T); % KL divergence. KL = -0.5 * sum(1 + logSigmaSq - mu.^2 - exp(logSigmaSq),1); KL = mean(KL); % Combined loss. loss = reconstructionLoss + KL; end
Model Predictions Function
The modelPredictions function takes as input the encoder and decoder network objects and minibatchqueue of input data mbq and computes the model predictions by iterating over all data in the minibatchqueue object.
function Y = modelPredictions(netE,netD,mbq) Y = []; % Loop over mini-batches. while hasdata(mbq) X = next(mbq); % Forward through encoder. Z = predict(netE,X); % Forward through decoder. XGenerated = predict(netD,Z); % Extract and concatenate predictions. Y = cat(4,Y,extractdata(XGenerated)); end end
Mini Batch Preprocessing Function
The preprocessMiniBatch function preprocesses a mini-batch of predictors by concatenating the input along the fourth dimension.
function X = preprocessMiniBatch(dataX) % Concatenate. X = cat(4,dataX{:}); end
See Also
trainnet | trainingOptions | dlnetwork | dlarray | adamupdate | dlfeval | dlgradient | sigmoid