Linearize Simulink Model to a Sparse Second-Order Model Object
This example shows how to linearize a Simulink® Model to obtain a sparse second-order model object (mechss). The Simulink model sparseSimulinkModel.slx contains a plant modeled using a Sparse Second Order block connected in a feedback loop with a PID controller and an actuator and sensor. The sensor and actuator are modeled using transfer functions. You need a Simulink Control Design™ license to perform linearization.
For more information on sparse models, see Sparse Model Basics.
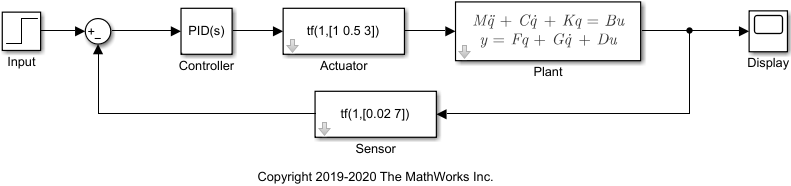
Load the model data contained in linData.mat and open the Simulink model.
load('linData.mat') mdl = 'sparseSimulinkModel'; open_system(mdl);
Next, construct the linearization I/O settings using linio (Simulink Control Design) and linearize the Simulink model.
sys_io(1) = linio('sparseSimulinkModel/Controller',1,'input'); sys_io(2) = linio('sparseSimulinkModel/Plant',1,'output'); sys = linearize(mdl,sys_io)
Sparse continuous-time second-order model with 1 outputs, 1 inputs, and 3415 degrees of freedom.
Use "spy" and "showStateInfo" to inspect model structure.
Type "properties('mechss')" for a list of model properties.
Type "help mechssOptions" for available solver options for this model.
The resultant linearized model sys is a mechss model object with 3415 degrees of freedom, 1 input and 1 output.
You can use spy to visualize the sparsity of the sparse model. Right-click on the plot to switch to select the matrices to be displayed.
spy(sys)

Use showStateInfo to view the partition information of the sparse second-order model sys.
showStateInfo(sys)
The state groups are:
Type Name Size
----------------------------------------------
Component 5
Component sparseSimulinkModel/Plant 3408
Signal 2
Examine the step response of the sparse second-order model. You must specify the final time or the time vector for sparse models.
t = 0:0.01:20; step(sys,t)

See Also
linearize (Simulink Control Design) | linio (Simulink Control Design) | mechss | showStateInfo | xsort | spy | Sparse Second
Order