Main Content

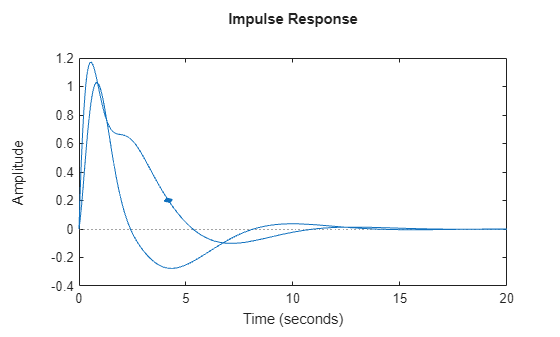
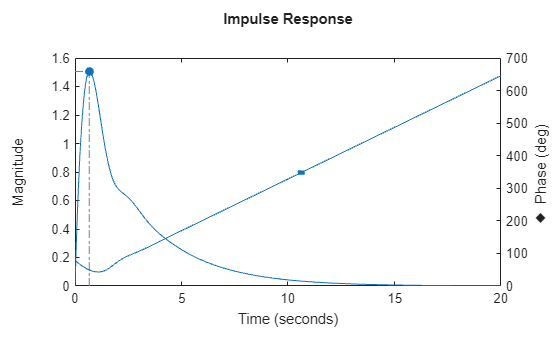
impulseplot

Plot impulse response of dynamic system

expand all in page

    Description

    The impulseplot function plots the impulse response of a dynamic system model and returns an ImpulsePlot chart object. To customize the plot, modify the properties of the chart object using dot notation. For more information, see Customize Linear Analysis Plots at Command Line.

    To obtain impulse response data or create an impulse plot with default plotting options, use impulse.

    Creation

    Syntax

    ip = impulseplot(sys)
    ip = impulseplot(sys1,sys2,...,sysN)
    ip = impulseplot(sys1,LineSpec1,...,sysN,LineSpecN)
    ip = initialplot(___,t)
    ip = impulseplot(sys,IC,t,p)
    ip = impulseplot(___,config)
    ip = impulseplot(___,plotoptions)
    ip = impulseplot(parent,___)

    Description

    ip = impulseplot(sys) plots the impulse response of the dynamic system model sys and returns the corresponding chart object.

    example

    ip = impulseplot(sys1,sys2,...,sysN) plots the impulse response of multiple dynamic systems sys1,sys2,…,sysN on the same plot.

    example

    ip = impulseplot(sys1,LineSpec1,...,sysN,LineSpecN) sets the line style, marker type, and color for the impulse response of each specified system.

    example

    ip = initialplot(___,t) simulates the response for the time steps specified by t. To define the time steps, you can specify:

    • Final simulation time using a scalar value.

    • The initial and final simulation times using a two-element vector. (since R2023b)

    • All the time steps using a vector.

    example

    ip = impulseplot(sys,IC,t,p) also specifies the parameter trajectory p for LPV models. (since R2023a)

    ip = impulseplot(___,config) specifies additional options for computing the step response, such as the step amplitude (dU) or input offset (U). Use RespConfig to create config.

    ip = impulseplot(___,plotoptions) plots the impulse response with the plotting options specified in plotoptions. Settings you specify in plotoptions override the plotting preferences for the current MATLAB® session. This syntax is useful when you want to write a script to generate multiple plots that look the same regardless of the local preferences.

    ip = impulseplot(parent,___) plots the impulse response in the specified parent graphics container, such as a Figure or TiledChartLayout, and sets the Parent property. Use this syntax when you want to create a plot in a specified open figure or when creating apps in App Designer.

    Input Arguments

    expand all

    Dynamic system, specified as a SISO or MIMO dynamic system model or array of dynamic system models. Dynamic systems that you can use include:

    • Continuous-time or discrete-time numeric LTI models, such as tf, zpk, or ss models.

    • Generalized or uncertain LTI models such as genss or uss models. (Using uncertain models requires Robust Control Toolbox™ software.)

      • For tunable control design blocks, the function evaluates the model at its current value for both plotting and returning response data.

      • For uncertain control design blocks, the function plots the nominal value and random samples of the model. When you use output arguments, the function returns response data for the nominal model only.

    • Sparse state-space models such as sparss and mechss models.

    • Identified LTI models, such as idtf, idss, or idproc models. For such models, the function can also plot confidence intervals and return standard deviations of the frequency response. See Step Responses of Identified Models with Confidence Regions. (Using identified models requires System Identification Toolbox™ software.)

    • Linear time-varying (ltvss) and linear parameter-varying (lpvss) models.

    This function does not support frequency-response data models such as frd, genfrd, or idfrd models.

    If sys is an array of models, the function plots the responses of all models in the array on the same axes. See Step Response of Systems in a Model Array.

    Line style, marker, and color, specified as a string or character vector containing symbols. The symbols can appear in any order. You do not need to specify all three characteristics (line style, marker, and color). For example, if you omit the line style and specify the marker, then the plot shows only the marker and no line.

    Example: '--or' is a red dashed line with circle markers

    Line StyleDescription
    "-"Solid line
    "--"Dashed line
    ":"Dotted line
    "-."Dash-dotted line
    MarkerDescription
    "o"Circle
    "+"Plus sign
    "*"Asterisk
    "."Point
    "x"Cross
    "_"Horizontal line
    "|"Vertical line
    "s"Square
    "d"Diamond
    "^"Upward-pointing triangle
    "v"Downward-pointing triangle
    ">"Right-pointing triangle
    "<"Left-pointing triangle
    "p"Pentagram
    "h"Hexagram
    ColorDescription
    "r"red
    "g"green
    "b"blue
    "c"cyan
    "m"magenta
    "y"yellow
    "k"black
    "w"white

    Time steps at which to compute the response, specified as one of the following:

    • Positive scalar tFinal— Compute the response from t = 0 to t = tFinal.

    • Two-element vector [t0 tFinal] — Compute the response from t = t0 to t = tFinal. (since R2023b)

    • Vector Ti:dt:Tf— Compute the response for the time points specified in t.

      • For continuous-time systems, dt is the sample time of a discrete approximation to the continuous system.

      • For discrete-time systems with a specified sample time, dt must match the sample time property Ts of sys.

      • For discrete-time systems with an unspecified sample time (Ts = -1), dt must be 1.

    • [] — Automatically select time values based on system dynamics.

    When you specify a time range using either tFinal or [t0 tFinal]:

    • For continuous-time systems, the function automatically determines the size of the time step and number of points based on the system dynamics.

    • For discrete-time systems with a specified sample time, the function uses the sample time of sys as the step size.

    • For discrete-time systems with unspecified sample time (Ts = -1), the function interprets tFinal as the number of sampling periods to simulate with a sample time of 1 second.

    Express t using the time units specified in the TimeUnit property of sys.

    If you specified a step delay td using config, the function applies the step at t = t0+td.

    Parameter trajectory of the LPV model, specified as a matrix or a function handle.

    • For exogenous or explicit trajectories, specify p as a matrix with dimensions N-by-Np, where N is the number of time samples and Np is the number of parameters.

      Thus, the row vector p(i,:) contains the parameter values at the ith time step.

    • For endogenous or implicit trajectories, specify p as a function handle of the form p = F(k,x,u) that gives parameters as a function of time sample k, state x, and input u. impulse only supports this option for discrete-time LPV models.

      This option is useful when you want to simulate quasi-LPV models.

    Configuration of the applied impulse signal, specified as a RespConfig object. By default, impulse applies an input at time t = 0. Use this input argument to change the response configuration, such as specifying a delay or input offset. See Configure Options for Impulse Response for an example.

    For lpvss and ltvss models with offsets (x0(t),u0(t)), you can use RespConfig to define the input relative to u0(t,p) and initialize the simulation with the state x0(t,p).

    Time response plot options, specified as a timeoptions object. You can use these options to customize the plot appearance. Settings you specify in plotoptions override the preference settings for the current MATLAB session.

    Parent container of the chart, specified as one of the following objects:

    • Figure

    • TiledChartLayout

    • UIFigure

    • UIGridLayout

    • UIPanel

    • UITab

    Properties

    expand all

    Note

    The properties listed here are only a subset. For a complete list, see ImpulsePlot Properties.

    Model responses, specified as an ImpulseResponse object or an array of such objects. Use this property to modify the dynamic system model or appearance for each response in the plot. Each ImpulseResponse object has the following fields.

    Source data for the response, specified as a structure with the following fields.

    Dynamic system, specified as a SISO or MIMO dynamic system model or array of dynamic system models.

    When you initially create a plot, Model matches the value you specify for sys.

    Time steps at which to compute the response, specified as one of the following:

    • Positive scalar tFinal— Compute the response from t = 0 to t = tFinal.

    • Two-element vector [t0 tFinal] — Compute the response from t = t0 to t = tFinal. (since R2023b)

    • Vector Ti:dt:Tf— Compute the response for the time points specified in t.

      • For continuous-time systems, dt is the sample time of a discrete approximation to the continuous system.

      • For discrete-time systems with a specified sample time, dt must match the sample time property Ts of sys.

      • For discrete-time systems with an unspecified sample time (Ts = -1), dt must be 1.

    • [] — Automatically select time values based on system dynamics.

    When you specify a time range using either tFinal or [t0 tFinal]:

    • For continuous-time systems, the function automatically determines the size of the time step and number of points based on the system dynamics.

    • For discrete-time systems with a specified sample time, the function uses the sample time of sys as the step size.

    • For discrete-time systems with unspecified sample time (Ts = -1), the function interprets tFinal as the number of sampling periods to simulate with a sample time of 1 second.

    Express t using the time units specified in the TimeUnit property of sys.

    If you specified a step delay td using config, the function applies the step at t = t0+td.

    Response configuration options, specified as a RespConfig object.

    Response name, specified as a string or character vector and stored as a string.

    Response visibility, specified as one of the following logical on/off values:

    • "on", 1, or true — Display the response in the plot.

    • "off", 0, or false — Do not display the response in the plot.

    The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.

    Option to list response in legend, specified as one of the following logical on/off values:

    • "on", 1, or true — List the response in the legend.

    • "off", 0, or false — Do not list the response in the legend.

    The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.

    Marker style, specified as one of the following values.

    MarkerDescription
    "none"No marker
    "o"Circle
    "+"Plus sign
    "*"Asterisk
    "."Point
    "x"Cross
    "_"Horizontal line
    "|"Vertical line
    "s"Square
    "d"Diamond
    "^"Upward-pointing triangle
    "v"Downward-pointing triangle
    ">"Right-pointing triangle
    "<"Left-pointing triangle
    "p"Pentagram
    "h"Hexagram

    Plot color, specified as an RGB triplet or a hexadecimal color code and stored as an RGB triplet.

    Alternatively, you can specify some common colors by name. The following table lists these colors and their corresponding RGB triplets and hexadecimal color codes.

    Color NameRGB TripletHexadecimal Color Code

    "red" or "r"

    		[1 0 0]#FF0000

    "green" or "g"

    		[0 1 0]#00FF00

    "blue" or "b"

    		[0 0 1]#0000FF

    "cyan" or "c"

    		[0 1 1]#00FFFF

    "magenta" or "m"

    		[1 0 1]#FF00FF

    "yellow" or "y"

    		[1 1 0]#FFFF00

    "black" or "k"

    		[0 0 0]#000000

    "white" or "w"

    		[1 1 1]#FFFFFF

    Line style, specified as one of the following values.

    Line StyleDescription
    "-"Solid line
    "--"Dashed line
    ":"Dotted line
    "-."Dash-dotted line

    Marker size, specified as a positive scalar.

    Line width, specified as a positive scalar.

    Response characteristics to display in the plot, specified as a CharacteristicsManager object with the following properties.

    Peak response, specified as a CharacteristicOption object with the following property.

    Peak response visibility, specified as one of the following logical on/off values:

    • "on", 1, or true — Display the peak response.

    • "off", 0, or false — Do not display the peak response.

    The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.

    Transient time, specified as a CharacteristicOption object with the following properties.

    Threshold for detecting steady state, specified as a scalar value between 0 and 1. For example, to measure when the response remains with 5% of the steady-state value, set a threshold value of 0.05.

    Transient time visibility, specified as one of the following logical on/off values:

    • "on", 1, or true — Display the peak response.

    • "off", 0, or false — Do not display the peak response.

    The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.

    Confidence region for identified models, specified as a CharacteristicOption object with the following properties.

    Confidence region visibility, specified as one of the following logical on/off values:

    • "on", 1, or true — Display the confidence region.

    • "off", 0, or false — Do not display the confidence region.

    The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.

    Number of standard deviations to display for the confidence region, specified as a positive scalar.

    Dependencies

    ConfidenceRegion is supported only for identified models, which require System Identification Toolbox software.

    Time units, specified as one of the following values:

    • "nanoseconds"

    • "microseconds"

    • "milliseconds"

    • "seconds"

    • "minutes"

    • "hours"

    • "days"

    • "weeks"

    • "months"

    • "years"

    Dependencies

    By default, the response uses the time units of the plotted linear system. You can override the default units by specifying toolbox preferences. For more information, see Specify Toolbox Preferences for Linear Analysis Plots.

    Option to normalize plot, specified as one of the following logical on/off values:

    • "on", 1, or true — Normalize the plot.

    • "off", 0, or false — Do not normalize the plot.

    The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.

    Chart visibility, specified as one of the following logical on/off values:

    • "on", 1, or true — Display the chart.

    • "off", 0, or false — Hide the chart without deleting it. You still can access the properties of chart when it is not visible.

    The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.

    Grouping of inputs and outputs pairs, specified as one of the following:

    • "none" — Do not group inputs or outputs.

    • "inputs" — Group only inputs.

    • "outputs" — Group only outputs.

    • "all" — Group all input-output pairs.

    Option to display inputs, specified as one of the following logical on/off values or an array of such values:

    • "on", 1, or true — Display the corresponding input.

    • "off", 0, or false — Hide the corresponding input.

    InputVisible is an array when the plotted system has multiple inputs. By default, all inputs are visible in the plot.

    The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState or an array of such values.

    Option to display outputs, specified as one of the following logical on/off values or an array of such values:

    • "on", 1, or true — Display the corresponding output.

    • "off", 0, or false — Hide the corresponding output.

    OutputVisible is an array when the plotted system has multiple outputs. By default, all outputs are visible in the plot.

    The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState or an array of such values.

    Object Functions

    addResponseAdd dynamic system response to existing response plot
    showConfidence (System Identification Toolbox)Display confidence regions on response plots for identified models

    Examples

    collapse all

    Open Live Script

    Generate a random state-space model with 5 states and create the impulse response plot with chart object ip.

    rng("default")
sys = rss(5);
ip = impulseplot(sys);

    MATLAB figure

    Change the time units to minutes and turn on the grid.

    ip.TimeUnit = "minutes";
grid on

    MATLAB figure

    The impulse plot automatically updates when you modify the chart object properties.

    Open Live Script

    For this example, consider a MIMO state-space model with 3 inputs, 3 outputs and 3 states. Create an impulse plot with red colored grid lines.

    Create the MIMO state-space model sys_mimo.

    J = [8 -3 -3; -3 8 -3; -3 -3 8];
F = 0.2*eye(3);
A = -J\F;
B = inv(J);
C = eye(3);
D = 0;
sys_mimo = ss(A,B,C,D);
size(sys_mimo)
    State-space model with 3 outputs, 3 inputs, and 3 states.

    Create an impulse plot with chart object ip and display the grid.

    ip = impulseplot(sys_mimo);
grid on

    MATLAB figure

    Set the grid color to red.

    ip.AxesStyle.GridColor = [1 0 0];

    MATLAB figure

    The impulse plot automatically updates when you modify the chart object. For MIMO models, impulseplot produces a grid of plots, each plot displaying the impulse response of one I/O pair.

    Open Live Script

    Compare the impulse response of a parametric identified model to a nonparametric (empirical) model, and view their 3-σ confidence regions. (Identified models require System Identification Toolbox™ software.)

    Identify a parametric and a nonparametric model from sample data.

    load iddata1 z1
sys1 = ssest(z1,4); 
sys2 = impulseest(z1);

    Plot the impulse responses of both identified models. Use the plot handle to display the 3-σ confidence regions.

    t = -1:0.1:5;
h = impulseplot(sys1,'r',sys2,'b',t);
showConfidence(h,3)
legend('parametric','nonparametric')

    MATLAB figure

    The nonparametric model sys2 shows higher uncertainty.

    Open Live Script

    For this example, examine the impulse response of the following zero-pole-gain model and limit the impulse plot to tFinal = 15 s. Use 15-point blue text for the title.

    sys = zpk(-1,[-0.2+3j,-0.2-3j],1)*tf([1 1],[1 0.05]);
tFinal = 15;

    Create the impulse response plot and specify the title size and color..

    ip = impulseplot(sys,tFinal);
ip.Title.FontSize = 15;
ip.Title.Color = [0 0 1];

    MATLAB figure

    Version History

    Introduced before R2006a

    See Also

    Topics