Train DQN Agent for Beam Selection
This example shows how to train a deep Q-network (DQN) reinforcement learning agent to accomplish the beam selection task in a 5G New Radio (NR) communications system. Instead of an exhaustive beam search over all the beam pairs, the trained agent increases beam selection accuracy by selecting the beam with highest signal strength while reducing the beam transitions based on the received RSRP. When you use an access network node (gNB) and a user equipment (UE) with 8 beams each, simulation results in this example show the trained agent selects beam pairs with greater than 80% maximum possible signal strengths and greater than 90% of the signal strength of the third optimal beam pair while reducing the beam switching frequency by 89%.
Introduction
To enable millimeter wave (mmWave) communications, beam management techniques must be used due to the high pathloss and blockage experienced at high frequencies. Beam management is a set of Layer 1 (physical layer) and Layer 2 (medium access control) procedures to establish and retain an optimal beam pair (transmit beam and a corresponding receive beam) for good connectivity [1]. For examples of NR beam management procedures, see NR SSB Beam Sweeping (5G Toolbox) and NR Downlink Transmit-End Beam Refinement Using CSI-RS (5G Toolbox).
This example considers beam selection procedures when a connection is established between the UE and gNB. In 5G NR, the beam selection procedure for initial access consists of beam sweeping, which requires exhaustive searches over all the beams on the transmitter and the receiver sides, and then selection of the beam pair offering the strongest reference signal received power (RSRP). Since mmWave communications require many antenna elements, implying many beams, an exhaustive search over all beams becomes computationally expensive and increases the initial access time.
To avoid repeatedly performing an exhaustive search and to reduce the communication overhead, this example uses a reinforcement learning (RL) agent to perform beam selection using the GPS coordinates of the receiver and the current beam angle while the UE moves around a track.
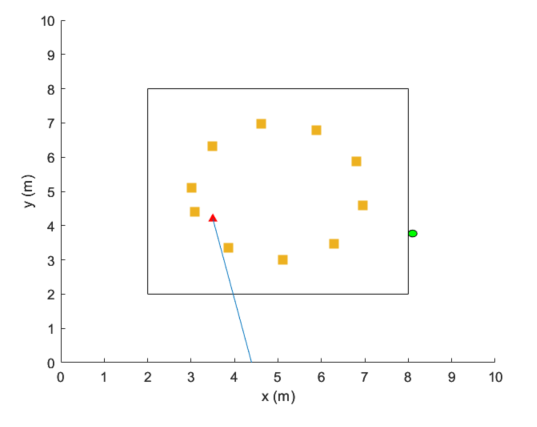
In this figure, the square represents the track that the UE (green circle) moves around, the red triangle represents the location of the base station (gNB), the yellow squares represent the channel scatterers, and the yellow line represents the gNB selected beam.
For more information on DQN reinforcement learning agents, see Deep Q-Network (DQN) Agent (Reinforcement Learning Toolbox).
Define Environment
To train a reinforcement learning agent, you must define the environment with which it will interact. The reinforcement learning agent selects actions given observations. The goal of the reinforcement learning algorithm is to find optimal actions that maximize the expected cumulative long-term reward received from the environment during the task. For more information about reinforcement learning agents, see Reinforcement Learning Agents (Reinforcement Learning Toolbox).
For the beam selection environment:
The observations are represented by UE position information and the current beam selection.
The actions are a selected beam out of 64 total beam pairs from the gNB and UE.
The reward at time step is given by:
is a reward for the signal strength measured from the UE (rsrp) if the agent selected the optimal beam, is a penalty for selecting a non-optimal action, and is a scaling factor.
The environment is created from the RSRP data generated using helperDQNBSGenerateData function. In the prerecorded data, receivers are randomly distributed on the perimeter of a 12-meter square and configured with 64 beam pairs (eight beams on each end, analog beamformed with one RF chain). Using a MIMO scattering channel, the example considers 10,000 receiver locations in the training set (DQNBS_TrainingData.mat) and 1000 receiver locations in the test sets (DQNBS_TestData.mat). The prerecorded data uses 2-D location coordinates.
The DQNBS_TrainingData.mat file contains a matrix of receiver locations, locationMatTrain, and an RSRP measurements of 64 beam pairs, rsrpMatTrain. Thus, the action space is 64 beam pair indices. You reorder the recorded data to imitate the receiver moving clockwise around the base station.
To generate new training and test sets, set useSavedData to false. Be aware that regenerating data can take up to a few hours.
% Set the random generator seed for reproducibility rng(0) useSavedData = true; if useSavedData % Load data generated from helperDQNBSGenerateData load DQNBS_TrainingData load DQNBS_TestData load DQNBS_position load DQNBS_txBeamAngle else % Generate data helperDQNBSGenerateData(); %#ok position.posTX = prm.posTx; position.ScatPos = prm.ScatPos; end txBeamAng = txBeamAng(1,:); % Sort location in clockwise order secLen = size(locationMatTrain,1)/4; [~,b1] = sort(locationMatTrain(1:secLen,2)); [~,b2] = sort(locationMatTrain(secLen+1:2*secLen,1)); [~,b3] = sort(locationMatTrain(2*secLen+1:3*secLen,2),"descend"); [~,b4] = sort(locationMatTrain(3*secLen+1:4*secLen,1),"descend"); idx = [b1;secLen+b2;2*secLen+b3;3*secLen+b4]; locationMat = locationMatTrain(idx,:); % Reshape RSRP for all transmit and receive beam pair indices and sort in clockwise order rsrpTrain = reshape(rsrpMatTrain, size(rsrpMatTrain,1)*size(rsrpMatTrain,2),[]); rsrpTrain = rsrpTrain(:,idx); % Agent step size during training simulation stepSize = size(locationMatTrain,1)/size(locationMatTest,1); % Create training environment using generated data envTrain = BeamSelectEnv(locationMat,rsrpTrain,position,txBeamAng,stepSize);
The environment is defined in the BeamSelectEnv supporting class, which is created using the rlCreateEnvTemplate class. BeamSelectEnv.m is located in this example folder. The reward and penalty functions are defined within and are updated as the agent interacts with the environment.
Create Agent
A DQN agent approximates the long-term reward for the given observations and actions by using a rlVectorQValueFunction (Reinforcement Learning Toolbox) critic. Vector Q-value function approximators have observations as inputs and state-action values as outputs. Each output element represents the expected cumulative long-term reward for taking the corresponding discrete action from the state indicated by the observation inputs.
The example uses the default critic network structures for the given observation and action specification.
obsInfo = getObservationInfo(envTrain); actInfo = getActionInfo(envTrain); agent = rlDQNAgent(obsInfo,actInfo); agent.ExperienceBuffer = rlPrioritizedReplayMemory(obsInfo,actInfo);
View the critic neural network.
criticNetwork = getModel(getCritic(agent)); analyzeNetwork(criticNetwork)
To foster exploration, the DQN agent in this example optimizes with a learning rate of 1e-3 and an epsilon decay factor of 3e-6. For a full list of DQN hyperparameters and their descriptions, see rlDQNAgentOptions (Reinforcement Learning Toolbox). Specify the agent hyperparameters for training.
if canUseGPU critic = getCritic(agent); critic.UseDevice = "gpu"; setCritic(agent, critic); end agent.AgentOptions.CriticOptimizerOptions.LearnRate = 1e-3; agent.AgentOptions.EpsilonGreedyExploration.EpsilonDecay = 3e-6; agent.AgentOptions.EpsilonGreedyExploration.EpsilonMin = 1e-3; agent.AgentOptions.NumStepsToLookAhead = 1; agent.AgentOptions.ExperienceBufferLength = 1e7; agent.AgentOptions.MiniBatchSize = 512; agent.AgentOptions.DiscountFactor = 0.99;
Train Agent
To train the agent, first specify the training options using rlTrainingOptions (Reinforcement Learning Toolbox). For this example, run each training session for at most 1000 episodes, with each episode lasting at most 1000 time steps, corresponding to one full loop of the track.
trainOpts = rlTrainingOptions(... MaxEpisodes=1000, ... MaxStepsPerEpisode=1000, ... % # of steps in testing dataset = 1000 StopTrainingCriteria="AverageReward", ... StopTrainingValue=10000, ... Plots="training-progress");
Train the agent using the train (Reinforcement Learning Toolbox) function. Training this agent is a computationally intensive process that takes several minutes to complete. To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true.
doTraining =false; if doTraining trainingStats = train(agent,envTrain,trainOpts); %#ok else load("DQNBS_TrainedAgent.mat") end
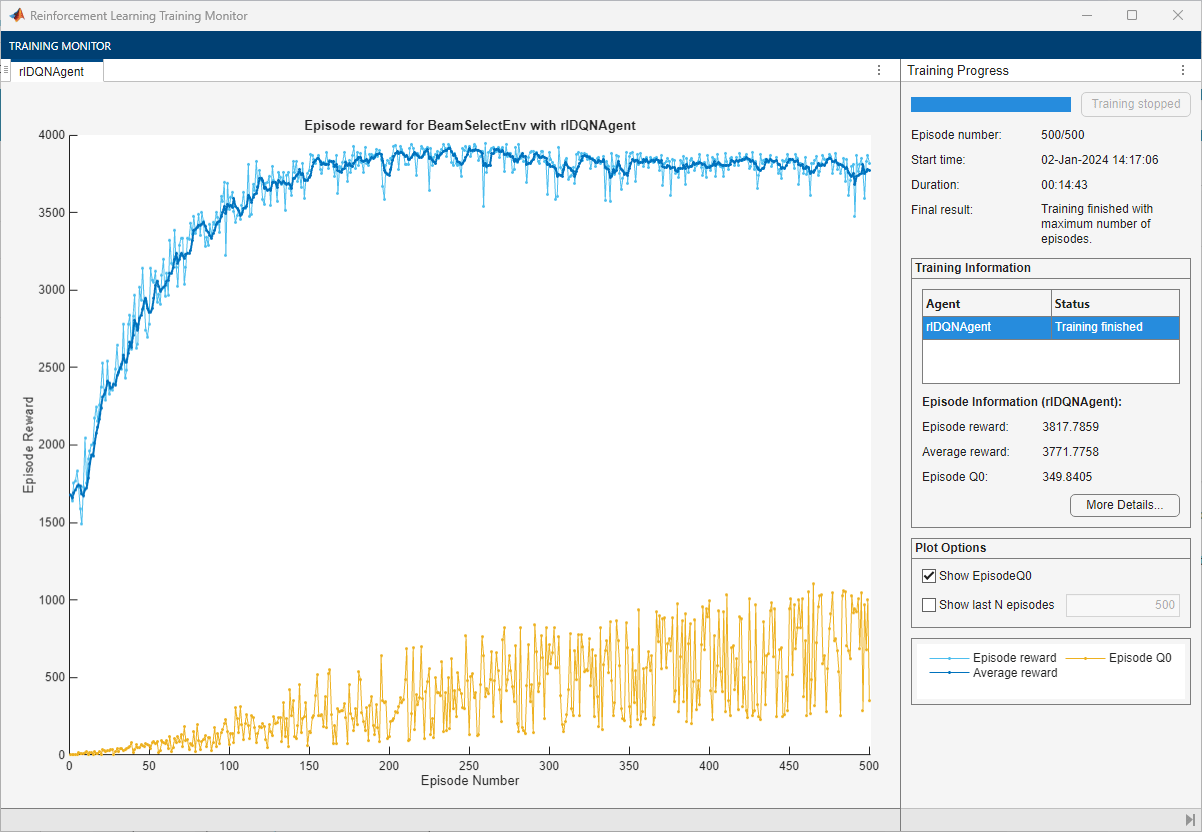
This figure shows the progression of the training. You can expect different results due to randomness inherent to the training process.
Simulate Trained Agent
To validate the trained agent, first set up a test environment with UE locations that the agent has not seen in the training process.
% Sort location in clockwise order secLen = size(locationMatTest,1)/4; [~,b1] = sort(locationMatTest(1:secLen,2)); [~,b2] = sort(locationMatTest(secLen+1:2*secLen,1)); [~,b3] = sort(locationMatTest(2*secLen+1:3*secLen,2),"descend"); [~,b4] = sort(locationMatTest(3*secLen+1:4*secLen,1),"descend"); idx = [b1;secLen+b2;2*secLen+b3;3*secLen+b4]; locationMat = locationMatTest(idx,:); % Reshape test RSRP values for all transmit and receive beam pairs and sort % in a clock-wise order rsrpTest = reshape(rsrpMatTest, size(rsrpMatTest,1)*size(rsrpMatTest,1),[]); rsrpTest = rsrpTest(:,idx); % Create test environment envTest = BeamSelectEnv(locationMat,rsrpTest,position,txBeamAng,1);
Simulate the environment with the trained agent. For more information on agent simulation, see rlSimulationOptions (Reinforcement Learning Toolbox) and sim (Reinforcement Learning Toolbox).
plot(envTest)
experience = sim(envTest,agent,rlSimulationOptions("MaxSteps",1000));
top3RSRP = maxk(squeeze(rsrpTest), 3, 1); top3TotalRSRP = sum(top3RSRP,2); rsrpSim = envTest.EpisodeRsrp; [top1rsrp,top1BeamIdx] = maxk((rsrpTest),1,1); stepAction=squeeze(experience.Action.act1.Data); resultsTable = table(rsrpSim/top3TotalRSRP(1), rsrpSim/top3TotalRSRP(2), rsrpSim/top3TotalRSRP(3), ... RowNames="Agent Total RSRP (%)", ... VariableNames=["Compared to 1st Optimal Beam Pair", "Compared to 2nd Optimal Beam Pair", "Compared to 3rd Optimal Beam Pair"]); disp(resultsTable)
Compared to 1st Optimal Beam Pair Compared to 2nd Optimal Beam Pair Compared to 3rd Optimal Beam Pair
_________________________________ _________________________________ _________________________________
Agent Total RSRP (%) 0.80559 0.85349 0.90792
disp("Agent reduced frequency of beam switching by " + num2str((1 - sum(diff(stepAction)>0)/sum(diff(top1BeamIdx)>0))*100) +"%")
Agent reduced frequency of beam switching by 89.0855%
References
[1] 3GPP TR 38.802. "Study on New Radio Access Technology Physical Layer Aspects." 3rd Generation Partnership Project; Technical Specification Group Radio Access Network.
[2] Sutton, Richard S., and Andrew G. Barto. Reinforcement Learning: An Introduction. Second edition. Cambridge, MA: MIT Press, 2020.
See Also
Topics
- Neural Network for Beam Selection (5G Toolbox)
- What Is Reinforcement Learning? (Reinforcement Learning Toolbox)
- Train Reinforcement Learning Agents (Reinforcement Learning Toolbox)
- Deep Learning in MATLAB (Deep Learning Toolbox)