Reconstruct 3-D Antenna Pattern from 2-D Slices Using Deep Learning

Since R2024a

This example shows how to use deep learning to reconstruct a 3-D antenna radiation pattern from two orthogonal 2-D slices. You then benchmark this reconstructed 3-D pattern against the results from a numerical simulation. The example includes these steps.

• Perform full-wave, electromagnetic simulation to generate 2-D slices of an antenna radiation pattern.

• Reconstruct the 3-D pattern from the 2-D slices using the patternFromAI function.

• Compare the predicted (reconstructed) pattern from the deep learning model to the actual (simulated) 3-D pattern from the numerical solution.

Note that the patternFromAI function uses a pretrained deep learning model trained on subsets of the Antenna Toolbox™ antenna and array catalogs. The training has taught the model the mapping between 2-D slices and their corresponding 3-D patterns across a broad range of antenna and array structures and variations of their design parameters. For more information on the pretrained deep learning model, see [1].

Background and Overview

Antenna radiation patterns are vital for evaluating the directional properties and overall performance of an antenna. Antenna patterns are often depicted using two principal cuts: the azimuthal (horizontal) and elevation (vertical) slices. These 2-D plots provide cross-sectional views of the antenna radiation characteristics along specific, orthogonal planes. However, a full 3-D pattern is sometimes essential for comprehensive design, analysis, and planning. A 3-D characterization typically demands extensive measurements or simulations that are both time-consuming and resource-intensive, especially in comparison to slice data. Sometimes, the 3-D pattern is simply unavailable, such as when antenna manufacturer datasheets or pattern files provide only the 2-D slice data.

Traditional approaches interpolate or reconstruct the 3-D pattern from the 2-D slices, and numerous analytical methods have been developed to perform this task—Antenna Toolbox provides two popular techniques in the patternFromSlices function. However, these traditional approaches have limitations in accuracy and generalizability, and make assumptions in the problem formulation. Reconstructing a 3-D pattern from its 2-D slices can be challenging due to the complexity of antenna radiation behavior and the potential for information loss in the process of taking the slices.

Advancements in deep learning and artificial intelligence provide promising solutions to these challenges. Deep learning models can learn and generalize complex relationships, such as the mapping between 2-D slices and their corresponding 3-D patterns, enabling accurate reconstruction despite limited data. The patternFromAI function uses a pretrained deep neural network to process the azimuthal and elevation cuts and reconstruct the full 3-D radiation pattern, and does not require extensive computational resources or deep learning expertise.

This example demonstrates the use of the patternFromAI function to reconstruct the 3-D radiation patterns of a rhombic antenna, specifically chosen for these reasons.

1. The radiation pattern of this antenna exhibits characteristics that challenge the limitations of the standard analytical pattern reconstruction methods.

2. The pretrained network has not seen or been trained on data from this specific antenna type. This test case highlights the ability of the network to generalize and its predictive capability when applied to new and unseen inputs.

3. You can simulate the rhombic antenna in Antenna Toolbox using the full-wave solver to obtain the actual 3-D pattern, which you can then use to compare and benchmark the accuracy of the prediction from the deep learning model.

Generate and Visualize 2-D Slice Data

Create the rhombic antenna object on which to perform full-wave electromagnetic simulation to generate the 2-D pattern slices for this example.

f = 6.11e9;
ant = design(rhombic,f);

Orient the antenna so that you can capture the key features of the 3-D pattern along both, or at least one of the principal planes, namely the azimuthal (X-Y) and elevation (X-Z) planes. When the 2-D slices contain the information about the primary radiation lobes, nulls, and other salient response behaviors, you can more accurately reconstruct the 3-D pattern. You can reasonably assume that a typical measurement setup would orient the antenna to capture the most important information along the principal planes used to represent the pattern characterization of the antenna.

ant.TiltAxis = [0 1 0];
ant.Tilt = 90;

Generate Horizontal Slice

Use the patternAzimuth function to compute the azimuthal pattern. Observe that the computation is quick, as the simulation for this 2-D slice contains only 361 points.

phi = 0:360;
az = phi;
tic
pA = patternAzimuth(ant,f,Azimuth=az);
toc

Elapsed time is 1.452866 seconds.

Use the polarpattern function to visualize the calculated azimuthal pattern.

figure
polarpattern(az,pA,TitleTop="Azimuthal Cut")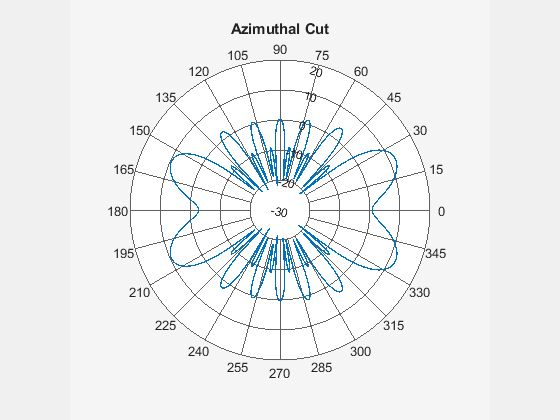

Generate Vertical Slice

Use the patternElevation function to compute the elevation pattern. Observe that the computation is quick, as the simulation for this 2-D slice contains only 361 points.

theta = 0:360;
el = 90-theta;
tic
pE = patternElevation(ant,f,Elevation=el);
toc

Elapsed time is 0.801387 seconds.

Use the polarpattern function to visualize the calculated elevation pattern.

figure
polarpattern(el,pE,TitleTop="Elevation Cut")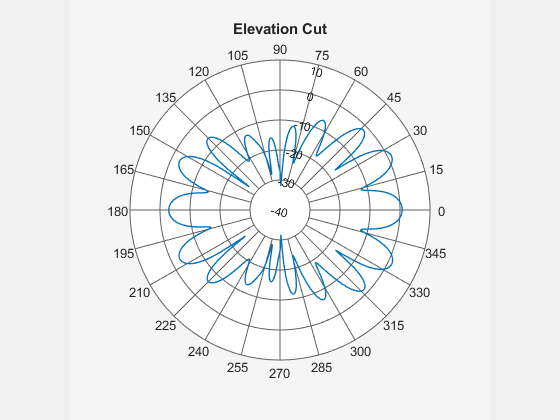

Examine Slice Data

Here are a few observations about the 2-D pattern slice data:

• The data contains many finely spaced side lobes, and the directivity pattern appears to have a complicated structure. You cannot easily discern how the 3-D pattern looks from the slices. To build the full 3-D pattern, you must use sophisticated reconstruction techniques.

• The main radiation lobes and maximum directivity are not along the boresight direction, namely the positive x-axis or $\left(\varphi ,\theta \right)=\left(0°,90°\right)$. This violates a key assumption of many traditional analytical methods, such as those used by the patternFromSlices function, rendering them ineffective.

• Radiation is similarly as strong in the back plane as it is in the front plane, and so the back plane data is important and cannot be ignored or discarded. However, many of the existing reconstruction techniques prioritize the front plane data and de-emphasize or do not account for the back plane data in one or both slices.

Reconstruct and Visualize 3-D Pattern Using Deep Learning

Use the patternFromAI function to predict the 3-D pattern using a deep-learning-based approach. Note that this step does not involve any full-wave electromagnetic simulation.

tic
[pR,thetaR,phiR] = patternFromAI(pE,theta,pA,phi);
toc

Elapsed time is 8.064804 seconds.

Use the patternCustom function to visualize the reconstructed pattern. Alternatively, you can call the patternFromAI function without any output arguments to directly visualize the reconstructed pattern. Observe that the reconstruction is relatively quick due to the fast inference time of the pretrained network.

figure
patternCustom(pR,thetaR,phiR)
title("Reconstructed 3-D Pattern — Deep Learning Model")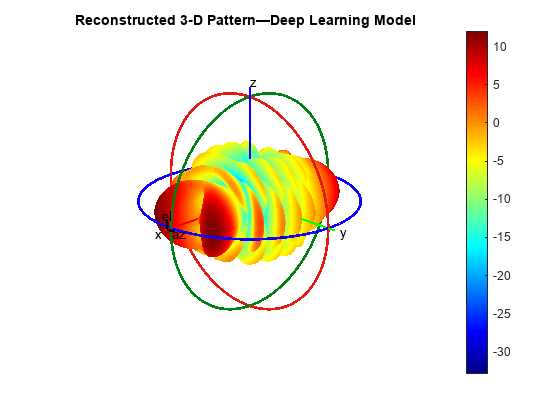

Compute and Visualize 3-D Pattern Using Full-Wave Simulation

Use the pattern function to perform full-wave electromagnetic simulation to compute the 3-D pattern of the rhombic antenna. Note that the elevation angles span only a 180° range to avoid redundancy in the spatial locations or angular directions, given that the azimuthal angles also span a 360° range. Observe that the computation is time-consuming due to the dense angular resolution of 361-by-181 points.

azR = phiR;
elR = 90-thetaR;
tic
p0 = pattern(ant,f,azR,elR);
toc

Elapsed time is 47.615554 seconds.

Use the patternCustom function to visualize the pattern data. First, transpose the output returned by the pattern function so that it is of size M-by-N, where M = numel(az) and N = numel(el). This facilitates a direct comparison to the prediction made by the patternFromAI function, which returns an output of size M-by-N.

p0 = p0.';
assert(isequal(size(pR),size(p0)))

figure
patternCustom(p0,thetaR,phiR)
title("Actual 3-D Pattern — Full-Wave Simulation")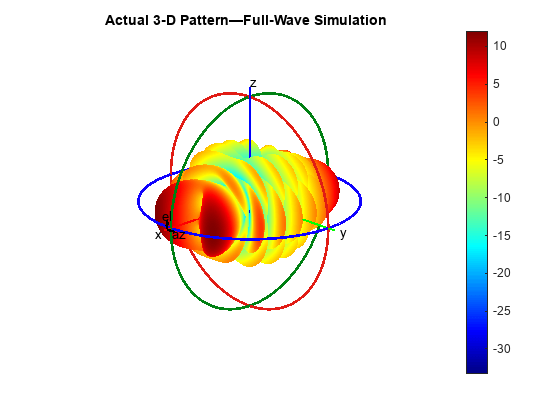

Compare Predicted and Actual 3-D Patterns

This example uses several visualization techniques and statistical metrics to compare the predicted (reconstructed) pattern from the deep learning model to the actual (simulated) pattern from numerical solution. Note that the actual pattern would generally not be available as a reference, or ground truth, for comparison, as the intention behind the deep learning model prediction is to create a reliable alternative to full 3-D pattern measurement or full-wave simulation. The purpose of the comparison in this example is to demonstrate that the patternFromAI function is capable of achieving strong reconstruction accuracy for antennas with high-complexity patterns.

Visualize Patterns Side-by-Side in Rectangular Coordinate System

Examine and compare the 3-D patterns as plotted in the rectangular coordinate system. As with the pattern plots seen earlier in the spherical coordinate system, the predicted and actual 3-D patterns are nearly indistinguishable upon visual comparison.

figure
tiledlayout(1,2)
nexttile
helperPatternCustomRectangular(pR,thetaR,phiR,"Predicted Pattern")
nexttile
helperPatternCustomRectangular(p0,thetaR,phiR,"Actual Pattern")

Visualize Directional Distribution of Absolute Prediction Error

Use the helperPatternCustomRectangular function, defined in the Supporting Functions section of this example, to plot the absolute error in the rectangular coordinate system as a function of the two angular coordinates. Overall, the reconstruction accuracy is very good.

figure
pAbsErr = abs(pR-p0);
helperPatternCustomRectangular(pAbsErr,thetaR,phiR,"Absolute Error (dBi)")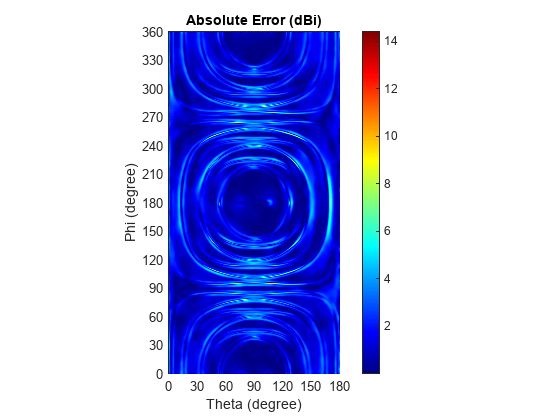

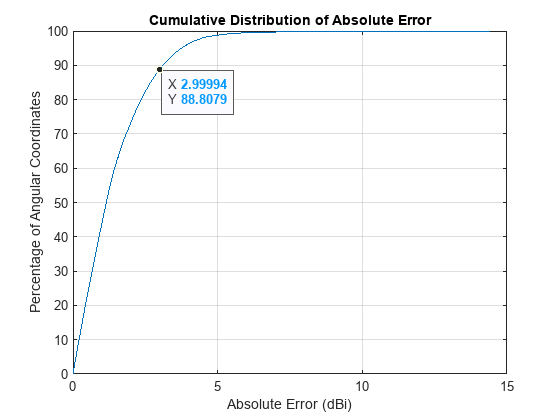
Create Cumulative Distribution Plot of Absolute Errors

Visualize the distribution of the errors in a cumulative distribution plot. Observe that the absolute prediction error is less than 3 dBi for more than 90% of the angular coordinates.

pAbsErrSorted = sort(pAbsErr(:));
nAbsErr = numel(pAbsErrSorted);
pAbsErrCDF = (1:nAbsErr)./nAbsErr*100;

figure
hPlot = stairs(pAbsErrSorted,pAbsErrCDF);
xlabel("Absolute Error (dBi)")
ylabel("Percentage of Angular Coordinates")
title("Cumulative Distribution of Absolute Error")
grid on

idx = find(pAbsErrSorted<=3,1,"last");
[~] = datatip(hPlot,DataIndex=idx);

Quantify Overall Prediction Accuracy Using Statistical Error Metrics

Calculate the root-mean-squared error (RMSE) and mean absolute error (MAE) over the entire 3-D pattern to quantify the overall prediction error. Both metrics are in units of dBi.

errorRMSE = sqrt(mean(pAbsErr.^2,"all"))

errorRMSE = 
1.6514

errorMAE = mean(pAbsErr,"all")

errorMAE = 
1.1457

Supporting Functions

The helperPatternCustomRectangular local function plots the angular distribution of the input quantity, such as directivity pattern or absolute error, in the rectangular coordinate system and configures some of the axes properties for display purposes.

function helperPatternCustomRectangular(p,theta,phi,titletext)
    patternCustom(p,theta,phi,CoordinateSystem="rectangular")
    title(titletext)
    view(2)
    colorbar
    xlim([-1 180])
    xticks(0:30:180)
    xtickangle(0)
    ylim([0 361])
    yticks(0:30:360)
    ytickangle(0)
    box on
end

References

[1] DiMeo, Peter, Sudarshan Sivaramakrishnan, and Vishwanath Iyer. “AI-Based 3D Antenna Pattern Reconstruction.” In 2024 IEEE International Symposium on Antennas and Propagation. Florence: IEEE, 2024.