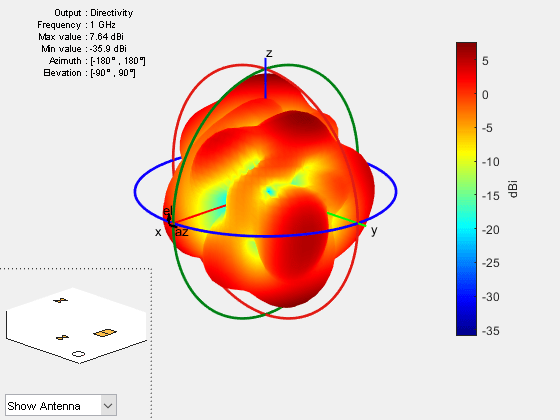
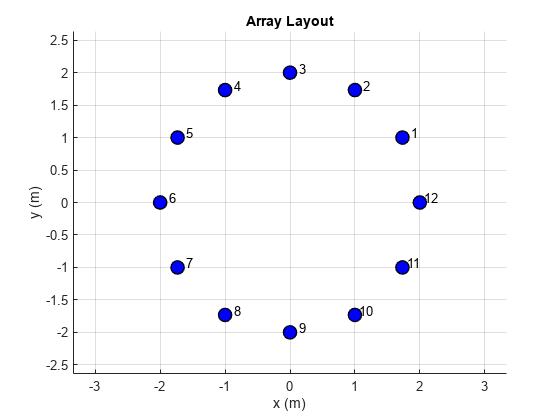
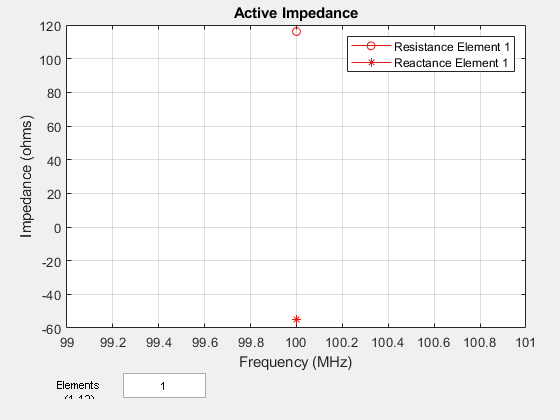
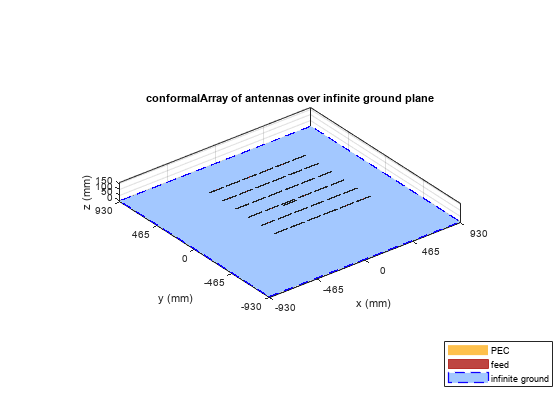
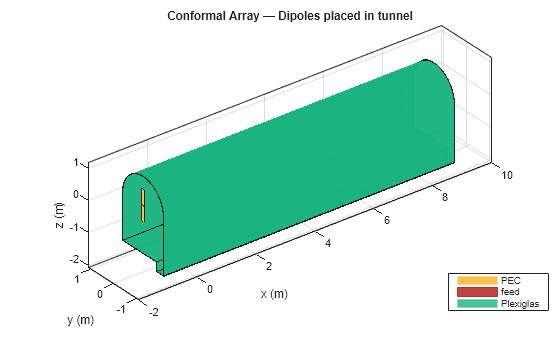
conformalArray
Create conformal array
Description
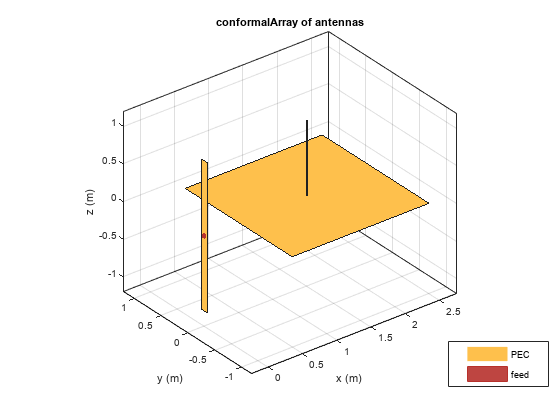
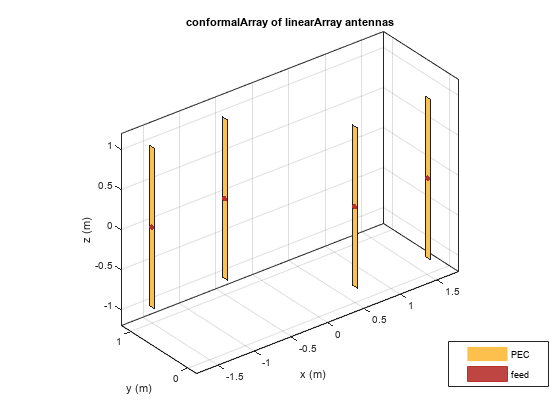
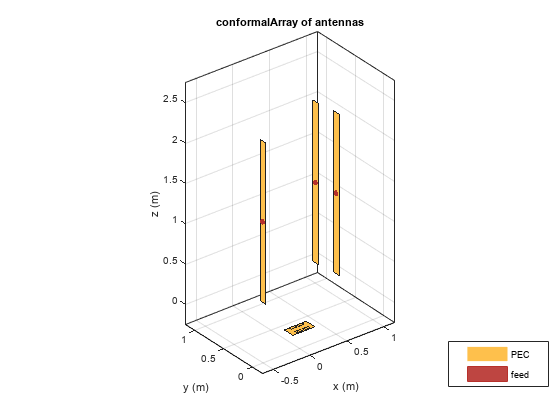
The conformalArray object creates a conformal array of the
specified antenna, array, or shape. You can also specify an array of any arbitrary
geometry, such as a circular array, a nonplanar array, an array with nonuniform
geometry, or a conformal array of arrays.
Conformal arrays are used in:
Direction-finding systems that use circular arrays or stacked circular arrays.
Aircraft systems due to surface irregularities or mechanical stress.
Creation
Description
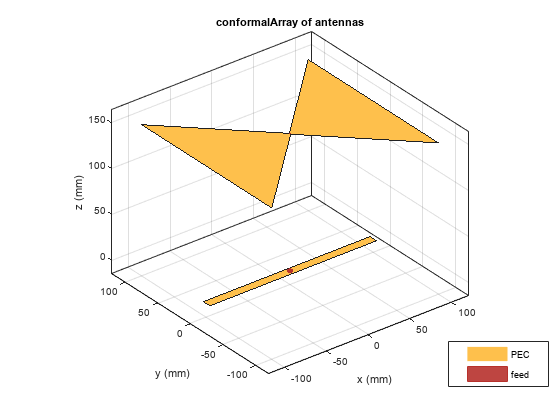
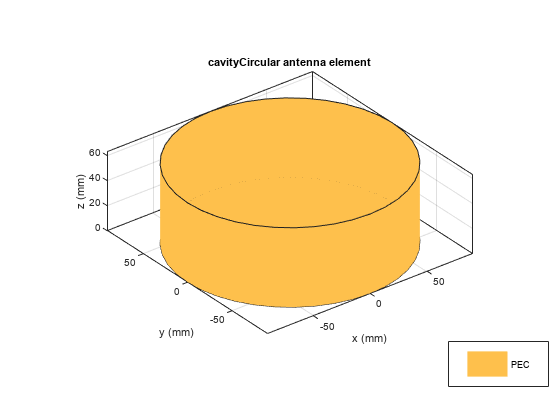
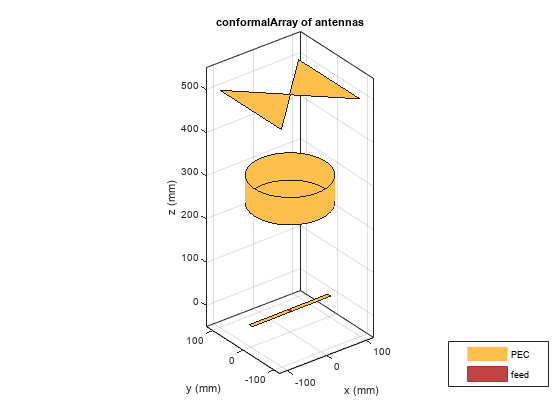
c = conformalArraydipole
object resonating around 700 MHz and a center-fed
bowtieTriangular object resonating around 403 MHz when
isolated. The antennas are spaced 0.15m apart from each other along the
positive z-axis.
c = conformalArray(PropertyName=Value)PropertyName is the
property name and Value is the corresponding value. You
can specify several name-value arguments in any order as
PropertyName1=Value1,...,PropertyNameN=ValueN.
Properties that you do not specify, retain default values.
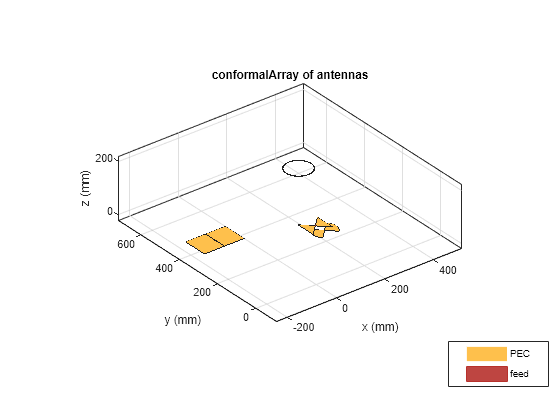
For example, c = conformalArray(Element={dipole
monopole},ElementPosition=[0,0,0.1; 0,0,0.2]) creates a
conformal array of a dipole and a monopole antenna whose feeds are at a
distance of 0.1 m and 0.2 m from the origin along the positive
z-axis.
Properties
Object Functions
arrayFactor | Array factor in dB |
axialRatio | Calculate and plot axial ratio of antenna or array |
beamwidth | Beamwidth of antenna |
charge | Charge distribution on antenna or array surface |
correlation | Correlation coefficient between two antennas in array |
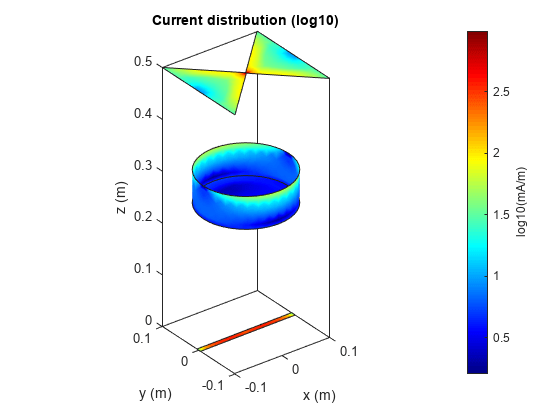
current | Current distribution on antenna or array surface |
design | Create antenna, array, or AI-based antenna resonating at specified frequency |
doa | Direction of arrival of signal |
efficiency | Calculate and plot radiation efficiency of antenna or array |
EHfields | Electric and magnetic fields of antennas or embedded electric and magnetic fields of antenna element in arrays |
feedCurrent | Calculate current at feed for antenna or array |
impedance | Calculate and plot input impedance of antenna or scan impedance of array |
info | Display information about antenna, array, or platform |
layout | Display array or PCB stack layout |
memoryEstimate | Estimate memory required to solve antenna or array mesh |
mesh | Generate and view mesh for antennas, arrays, and custom shapes |
meshconfig | Change meshing mode of antenna, array, custom antenna, custom array, or custom geometry |
msiwrite | Write antenna or array analysis data to MSI planet file |
optimize | Optimize antenna and array catalog elements using SADEA or TR-SADEA algorithm |
pattern | Plot radiation pattern of antenna, array, or embedded element of array |
patternAzimuth | Azimuth plane radiation pattern of antenna or array |
patternElevation | Elevation plane radiation pattern of antenna or array |
patternMultiply | Radiation pattern of array using pattern multiplication |
peakRadiation | Calculate and mark maximum radiation points of antenna or array on radiation pattern |
phaseShift | Calculate phase shift values for arrays or multi-feed PCB stack |
rcs | Calculate and plot monostatic and bistatic radar cross section (RCS) of platform, antenna, or array |
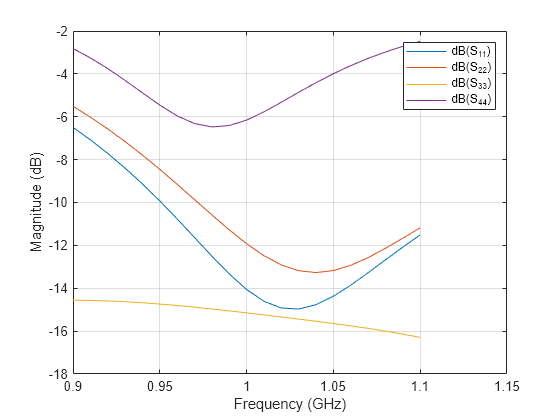
returnLoss | Calculate and plot return loss of antenna or scan return loss of array |
show | Display antenna, array structures, shapes, or platform |
sparameters | Calculate S-parameters for antenna or array |
stlwrite | Write mesh information to STL file |
vswr | Calculate and plot voltage standing wave ratio (VSWR) of antenna or array element |
Examples
Create a default conformal array.
c = conformalArray
c =
conformalArray with properties:
Element: {[1×1 dipole] [1×1 bowtieTriangular]}
ElementPosition: [2×3 double]
Reference: 'feed'
AmplitudeTaper: 1
PhaseShift: 0
Tilt: 0
TiltAxis: [1 0 0]
show(c)
This example shows how to create a conformal array consisting of bowtieRounded, bowtieTriangular, dipoleBlade, and loopCircular antennas operating at 1 GHz. The same workflow using Antenna Array Designer app is also shown in a complementary video.
Video Walkthrough
For a walkthrough of the example, play the video.
In this video, we are going to design the conformalArrays with the antennaArrayDesigner app. conformalArray is the antenna toolbox functionality which allows the user to create an array with different antenna elements. The array can have an arbitrary geometry. It can be a non-planar array or an array with non-uniform geometry. This is a documentation page for the conformalArray.
And you can see that we have shown a default conformalArray with a dipole and a bow-tie triangular antenna element. In this way, you can create arrays with different antenna elements, and you can place them at any arbitrary locations to create an array. Now, let us go to the antenna array designer app and let us create a conformalArray.
Type the antennaArrayDesigner in the command line and hit Enter. Once the antennaArrayDesigner app opens up, we will start designing the conformalArray. The antennaArrayDesigner has opened. And in order to start the design, click on the plus symbol. Now the antenna antennaArrayDesigner layout page has opened. And in this page, you can start creating the conformalArray.
In the first section, you have something called as the array type where you can select the conformalArray. Once you select the conformalArray, there are two windows that open up. One is the layout window, and second one is the array window. So in this particular window, you can see that there are two antennas. One is the dipole, and the other one is the bow-tie triangular element.
The layout window shows the location of these antenna elements in all the three planes. You can interactively select any one of the antenna element here, and you can change the antenna element. You can move the positions of the antenna elements, or you can add additional antenna elements using this canvas. First, I'll select one of the elements from here, and then I will change that element to a different antenna.
So whenever I move the mouse over these blue dots, you can see that it shows the name of that antenna and the location of that antenna. So I'll just select the dipole here and change the dipole to a bow-tie-rounded antenna. So once I select on this, you can see that the dipole is changed to the bow-tie-rounded, and that particular element is shown here.
Now, you can also change the position of these antenna elements interactively using this canvas. So I will just move this position one from 0 to 0.15 on the x-axis. Once I move here, you can see that automatically the 3D layout of these antennas changes.
You can also move the antennas on the yz plane and on the xy plane. So if you want to move the antennas on the xy plane, I can click this and place it on 0.15 on both x and y. Once I do that, automatically the 3D geometry changes here. And the two antennas are now placed at the location selected on the canvas. In this way, the canvas can be interactively used to change the locations of the array and also be used to change the elements.
Now that we have changed the location and we have also changed one of the element, let us add additional elements into this particular array layout. And then we will design this particular array at a specific frequency. So click on the canvas such that the elements are unselected. Now click on the dropdown here, and you can select any one of these antennas from the given antennas. And you can bring those into the canvas.
For now, I will select a blade dipole antenna. I will click on that antenna. And as soon as I click on it, there is a message on the canvas saying, "place antenna on the canvas." So I can select any arbitrary location here, and I can place the antenna. So for now, I will select the location that is minus 0.1 and 0.4, and I'll click on that particular location.
Once I click on that location, you can see that a blade dipole is created here at that specific location. The antenna can be rotated later whenever we go into the next pane. Now, let us add another antenna. So I will again click on the canvas so that the element is unselected. And I will again click on the dropdown here. And from the dropdown, I will select any one of the antenna.
I will click on the loop antenna, and I will place the antenna on the canvas here. Once I click on 0.4 ,0.6 on the canvas, a loop antenna will be created there. As you can see, the dimensions of these antennas are set at different frequencies. But once we design it at a specific frequency, all the antenna dimensions will be calculated for that frequency.
Now, out of the four antennas that we have selected, from the canvas you can also right click, and you can change the properties of those elements, that is, you can delete the element. You can add backing to that element. So these are all the options that you can exercise from the canvas. Now, let us keep the antenna elements as it is. And I will change the design frequency to 1 gigahertz, and I will click on Accept.
Now all the four antenna dimensions will be designed at 1 gigahertz. And in the next pane, we will see the finalized dimensions. So these are the calculated dimensions at 1 gigahertz. And you can see that our array contains four different elements which are placed at arbitrary locations.
On the left hand side, you can see the properties panel, which shows the properties from the conformalArray and the properties of the individual elements. The first element here is the element position. And the element position is shown for all the elements. The reference is set at origin. And the amplitude taper and the phase shift for the array is given. And the tilt and tilt axes are given.
In the dropdown, you can see the elements that are present in the array. So you see that the first element is the bow-tie-round, bow-tie triangular dipole blade, and loop antenna. Whichever element is selected here, that element's properties can be accessed in this particular section. Now, the bow-tie-rounded is selected and the properties of the bow-tie-rounded can be accessed in the next dropdown.
So you can see that the properties of the bow-tie-rounded are shown here. And you can change the orientation of the antenna by changing the tilt and tilt axis. Now let us change the orientation of the blade dipole. For this, I will just click on the dropdown and then go to the blade dipole. And I'll select the orientation of the blade dipole to be 90 degrees with respect to y-axis. So I will just make the tilt axis as 0.10.
So I have changed the tilt to 90 and the axis to y-axis. Once I hit Apply, you can see that the blade dipole is now on the xy plane. So this is the array structure that we have, and this is a totally arbitrary array that we are considering. But this particular exercise is to show you that any arbitrary array can be created. Now, you can also change the conductor of this particular element, and you can apply the load for any of these antenna elements.
Now let us start analyzing the structure and calculate the S-parameters for this particular array. So on the toolstrip, you can see that the center frequency is given as 1 gigahertz, which is our design frequency. And the frequency range is given from 900 megahertz to 1,100 megahertz. Click on the S-parameters button to calculate the s parameters of these antennas. The S-parameters of the antennas are calculated. And you can see that the S-parameters are plotted for four antennas.
So we have total of 16 S-parameter curves. If you want to visualize only the return loss for four antennas, then we will just select all the other parameters. So just click on the other S-parameters, which we don't want to visualize so that those will be hidden from this particular display. I just select S1, S2 to S33 and S44.
As you can see here, the return loss for these antennas is below minus 10 dB at 1 gigahertz. But the fourth antenna, the S44, is having a poor return loss. So the fourth antenna that we have is a loop circular. And we all know that a loop circular antenna is not matched properly. Now, let us take a look at the radiation pattern for these antennas.
Click on the 3D pattern here to calculate the radiation pattern for this particular array. Because we have randomly selected the elements and we have placed at arbitrary locations-- the radiation pattern will also look arbitrary. So as you can see here, the radiation pattern is plotted. And the maximum value of the gain we are seeing here is 7.54 dBi. But the direction is pretty random as we have placed the antennas at random locations. You can also plot azimuth and elevation pattern for this particular array.
If you are satisfied with your design, then you can click the Export button. And you can export this design to the workspace or you can export this design as a script. Once you export this design as a script, then you can add additional script. And you can also do parametric analysis of the antenna and plot the results like gain versus frequency or S-parameters for different frequencies. In this way, you can design the conformalArray with an arbitrary geometry and a non-planar structure using the antennaArrayDesigner app within a matter of minutes and analyze those antennas.
Design and Analysis Workflow
Define the analysis frequency range.
f = 900e6:10e6:1.1e9;
Design and orient the rounded bowtie, triangular bowtie, blade dipole, and circular loop antennas.
% Rounded bowtie antenna br = design(bowtieRounded,f(11)); br.Tilt = 90; br.TiltAxis = [0 1 0]; % Triangular bowtie antenna bt = design(bowtieTriangular,f(11)); bt.Tilt = 90; bt.TiltAxis = [0 1 0]; % Blade dipole antenna db = design(dipoleBlade,f(11)); db.Tilt = 90; db.TiltAxis = [0 1 0]; % Circular loop antenna lc = design(loopCircular,f(11));
Create a conformal array.
c = conformalArray(Element={br bt db lc},...
ElementPosition=[0.2189 0.2318 0; 0 0 0.2; -0.1 0.4 0; 0.4 0.6 0],Reference="origin")c =
conformalArray with properties:
Element: {[1×1 bowtieRounded] [1×1 bowtieTriangular] [1×1 dipoleBlade] [1×1 loopCircular]}
ElementPosition: [4×3 double]
Reference: "origin"
AmplitudeTaper: 1
PhaseShift: 0
Tilt: 0
TiltAxis: [1 0 0]
Visualize the conformal array.
show(c)
Plot the S-parameters of this array in the 900 MHz to 1.1 GHz range.
s = sparameters(c,f);
figure
rfplot(s,{[1,1];[2,2];[3,3];[4,4]});
Plot the radiation pattern of this array at 1 GHz.
pattern(c,f(11))
Define the radius and the number of elements for the array.
r = 2; N = 12;
Create an array of 12 dipoles.
elem = repmat(dipole(Length=1.5),1,N);
Define the x,y,z values for the element positions in the array.
del_th = 360/N; th = del_th:del_th:360; x = r.*cosd(th); y = r.*sind(th); z = ones(1,N); pos = [x;y;z];
Create a circular array using the defined dipoles and then visualize it. Display the layout of the array.
c = conformalArray(Element=elem,ElementPosition=pos'); show(c)
figure layout(c)
Change the width of the fourth and the twelfth element of the circular array. Visualize the new arrangement.
c.Element(4).Width = 0.05; c.Element(12).Width = 0.2; figure show(c)
Calculate and plot the impedance of the circular array at 100 MHz. The plot shows the impedance of the first element in the array.
figure impedance(c,100e6)
To view the impedance of all the elements in the array change the value from 1 to 1:12 as shown in the figure.
Define three circular loop antennas of radii 0.6366 m (default), 0.85 m, and 1 m, respectively.
l1 = loopCircular; l2 = loopCircular(Radius=0.85); l3 = loopCircular(Radius=1);
Create a concentric array that uses the origin of circular loop antennas as its position reference.
c = conformalArray(Element={l1 l2 l3},ElementPosition=[0 0 0; 0 0 0;...
0 0 0],Reference="origin");
show(c)
Visualize the radiation pattern of the array at 80 MHz.
pattern(c,80e6)
Create a dipole antenna to use in the reflector and the conformal array.
d = dipole(Length=0.13,Width=5e-3,Tilt=90,TiltAxis='Y');Create an infinite groundplane reflector antenna using the dipole as exciter.
rf = reflector(Exciter=d,Spacing=0.15/2,GroundPlaneLength=inf);
Create a conformal array using 36 dipole antennas and one infinite groundplane reflector antenna. View the array.
x = linspace(-0.4,0.4,6); y = linspace(-0.4,0.4,6); [X,Y] = meshgrid(x,y); pos = [X(:) Y(:) 0.15*ones(numel(X),1)]; for i = 1:36 element{i} = d; end element{37} = rf; lwa = conformalArray(Element=element,ElementPosition=[pos; 0 0 0.15/2]); show(lwa)
Drive only the reflector antenna with an amplitude of 1.
V = zeros(1,37); V(end) = 1; lwa.AmplitudeTaper = V;
Compute the radiation pattern of the conformal array.
figure
pattern(lwa,1e9,Type='efield')
Create two patch microstrip antennas using dielectric substrate FR4. Tilt the second patch microstrip antenna by 180 degrees.
p1 = patchMicrostrip(Substrate=dielectric('FR4')); p2 = patchMicrostrip(Substrate=dielectric('FR4'),Tilt=180);
Create and view a conformal array using the two patch microstrip antennas placed 11 cm apart.
c = conformalArray(ElementPosition=[0 0 0; 0 0 0.1100],Element={p1 p2});
show(c)
Create a conformal array using dipole and monopole antennas and display it.
c = conformalArray(Element={dipole monopole},...
ElementPosition=[0 0 0; 1.5 0 0]);
show(c)
Plot the radiation pattern of the array at 70 MHz.
pattern(c,70e6)
Create a subarray of linear arrays at different locations.
la = linearArray(ElementSpacing=1)
la =
linearArray with properties:
Element: [1×1 dipole]
NumElements: 2
ElementSpacing: 1
AmplitudeTaper: 1
PhaseShift: 0
Tilt: 0
TiltAxis: [1 0 0]
subArr = conformalArray(Element=[la la],ElementPosition=[1 0 0; -1 1 0])
subArr =
conformalArray with properties:
Element: [1×2 linearArray]
ElementPosition: [2×3 double]
Reference: 'feed'
AmplitudeTaper: 1
PhaseShift: 0
Tilt: 0
TiltAxis: [1 0 0]
show(subArr)
Create a linear array of dipoles with and element spacing of 1m.
la = linearArray(ElementSpacing=1);
Create a rectangular array of microstrip patch antennas.
ra = rectangularArray(Element=patchMicrostrip,RowSpacing=0.1,ColumnSpacing=0.1);
Create a subarray containing the above linear and rectangular arrays with changes in amplitude taper and phase shift values.
subArr = conformalArray(Element={la ra dipole},ElementPosition=[0 0 1.5; 0 0 0; 1 1 1],...
AmplitudeTaper=[3 0.3 0.03],PhaseShift=[90 180 120]);
show(subArr)
This example shows how to create a circular cavity structure as an element in a conformalArray and plot its surface current distribution.
Create Circular Cavity Antenna
Create a circular cavity antenna operating at 1 GHz using the design function and the cavityCircular element from the antenna catalog. Display the antenna.
f = 1e9; lambda = 3e8/f; ant = design(cavityCircular,f); figure show(ant)
Derive Backing Structure
Derive the circular cavity backing structure from the cavity antenna by specifying the 'Exciter' property as an empty array. Display the backing structure.
ant.Exciter = []; figure show(ant)
Create Conformal Array
Create and display a conformal array with circular cavity as one of its elements.
ca = conformalArray;
ca.Reference = "origin";
ca.ElementPosition = [0 0 0; 0 0 0.25; 0 0 0.5];
ca.Element = {ca.Element{1} ant ca.Element{2}};
figure
show(ca)
Plot Surface Current Distribution
Calculate the current at the feed location and plot the surface current distribution of the conformal array at 1 GHz.
If = feedCurrent(ca,f)
If = 1×2 complex
0.0023 - 0.0005i 0.0029 + 0.0007i
figure
current(ca,f,Scale="log10")
This example shows how to create a conformal array of antennas and a geometric structure. This example uses two dipole antennas and a Plexiglas tunnel for the demonstration. The dipole antennas are placed at the openings of the tunnel.
Define the dimensions in meters.
domeRadius = 1.8/2; outlineWidth = 1.5; cavityLength = 0.3; cavityWidth = 0.3; thickness = 0.01; tunnelLength = 10;
Create two tunnel faces with slightly different dimensions. Then subtract smaller face from the larger to get an outline of the tunnel with specified thickness. Create shapes for tunnel dome, wall, and cavity. Add them together to get the overall shape.
Create smaller tunnel face.
tunnelDome = shape.Circle(Radius=domeRadius); tunnelWall = shape.Rectangle(Length=domeRadius*2,Width=outlineWidth); [~] = translate(tunnelWall,[0 -tunnelWall.Width/2 0]); tunnelCavity = shape.Rectangle(Length=cavityLength,Width=cavityWidth); [~] = translate(tunnelCavity,[-tunnelWall.Length/2+tunnelCavity.Length/2 ... -tunnelWall.Width-tunnelCavity.Width/2 0 ]); tunnelSmall = tunnelDome + tunnelWall + tunnelCavity; figure show(tunnelSmall) title("Smaller Tunnel Face")
Create larger tunnel face.
tunnelDome = shape.Circle(Radius=domeRadius+thickness); tunnelWall = shape.Rectangle(Length=domeRadius*2+thickness*2,Width=outlineWidth+thickness); [~] = translate(tunnelWall,[0 -tunnelWall.Width/2 0]); tunnelCavity = shape.Rectangle(Length=cavityLength+thickness*2,Width=cavityWidth); [~] = translate(tunnelCavity,[-tunnelWall.Length/2+tunnelCavity.Length/2 ... -tunnelWall.Width-tunnelCavity.Width/2 0 ]); tunnelLarge = tunnelDome + tunnelWall + tunnelCavity; figure show(tunnelLarge) title("Larger Tunnel Face")
Subtract smaller face from larger to get an outline of the tunnel with 0.01 m thickness.
tunnelOutline = tunnelLarge - tunnelSmall;
show(tunnelOutline)
title("Outline of Tunnel with 0.01 m Thickness")
Linearly extrude the outline to generate a 10 m. long tunnel. Specify Plexiglas as the dielectric material of the tunnel using the Dielectric property. You can add any dielectric material from the dielectric catalog. To view a list of dielectric materials, run openDielectricCatalog on the command line.
tunnelOutline = removeSlivers(tunnelOutline,1e-12); tunnel = extrudeLinear(tunnelOutline,tunnelLength,Caps=true)
tunnel =
Custom3D with properties:
Name: 'custom3D'
Vertices: [80×3 double]
Metal: 'PEC'
Dielectric: 'Air'
FrequencyModel: 'Constant'
Color: 'y'
Transparency: 1
EdgeColor: 'k'
tunnel.Dielectric="Plexiglas";Orient the tunnel.
[~] = rotateY(tunnel,90); rotateX(tunnel,90);
Create a conformal array with two dipoles and the tunnel as its elements.
c = conformalArray; c.ElementPosition = [-1 0 0;-1 0 0;8 0 0]; c.Reference = "origin"; c.Element = {dipole(Length=1),tunnel,dipole(Length=1)}; figure show(c) title("Conformal Array — Dipoles placed in tunnel")
Mesh the conformal array. You can control the mesh of individual elements by specifying a vector of edge lengths.
mesh(c,MaxEdgeLength=[0.05 0.2 0.05]);
More About
Reference property of
conformalArray object defines the position reference of an
antenna element in 3–D space. You can position the antenna by specifying the
Reference property as "feed" or
"origin".
Choose the position reference as "feed" to move the antenna
element with respect to the feed point so that the new feed location is at the
specified coordinates. Following diagram shows a rectangular loop antenna and
reflector-backed antenna before and after relocation with respect to the feed
point:
Choose the position reference as "origin" to move the antenna
element so that new antenna origin is at the specified coordinates. Following
diagram shows a rectangular loop antenna and a reflector-backed antenna before and
after the relocation with respect to origin:
References
[1] Balanis, Constantine A. Antenna Theory: Analysis and Design. 3rd Ed. New York: John Wiley and Sons, 2005.
Version History
Introduced in R2016a
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: United States.
You can also select a web site from the following list
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)