Optimize a Satellite Constellation While Satisfying Constraints on Ground Station Access
This example shows how to use a Global Optimization Toolbox solver with Aerospace Toolbox™ functions to find a minimal satellite constellation that meets ground station access requirements. The example assumes that a ground station network of four stations is given. A more elaborate optimization might include allocating ground stations as well as satellites. The access requirements are:
Several points of interest must be observable from the satellites for at least a fixed percentage of the time. In this example, the points of interest are the ground stations.
Each satellite must view a ground station for at least a fixed percentage of the time to download its data. You can calculate these percentages using the
accessPercentagefunction.
All satellites are at the same altitude, and the altitude is one of the optimization variables. The satellites are also at the same orbital inclination, another optimization variable. The satellites are in a number of orbital planes, an optimization variable that is an integer no more than 10. Finally, the number of satellites per orbital plane is an optimization variable, an integer no more than 20.
The objective is to minimize the total number of satellites.
Constellation Definition
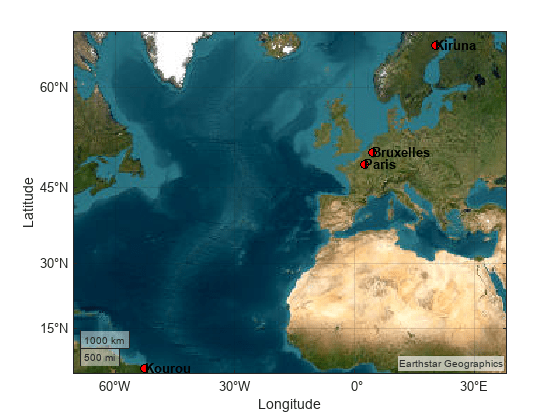
Place the coordinates of the four ground stations in the workspace. Plot the ground stations on a map.
targets = table(... Size=[0,3],... VariableTypes=["string","double","double"],... VariableNames=["Name","Latitude","Longitude"]); targets(1:4,:) = {... "Paris", 48.856614, 2.3522219 ; "Bruxelles", 50.850340, 4.351710 ; "Kiruna", 64.8557995, 20.2252821 ; % Far from the equator "Kourou", 5.1597, -52.6503 }; % Close to the equator figure; geoaxes("Basemap","satellite"); geoplot(targets.Latitude, targets.Longitude,"ko",MarkerFaceColor="red"); % Annotate the targets. text(targets.Latitude,targets.Longitude,targets.Name,FontWeight="bold");
The ground stations must be observable by at least one satellite for at least minObservability = 90% of the time. To calculate whether this constraint is satisfied for a constellation, use the observability helper function at the end of this example. The function uses the satellite scenario function walkerDelta and access methods available in Aerospace Toolbox.
minObservability = 0.9;
Define the satellite scenario and include the specified targets as ground stations. Bundle the scenario and target objects into a structure named mission.
% Setup scenario mission.Scenario = satelliteScenario(... datetime(2023,09,02,12,0,0),... datetime(2023,09,02,12,0,0) + days(1),... 300); % Ground stations mission.Targets = groundStation(... mission.Scenario,... Name=targets.Name,... Latitude=targets.Latitude,... Longitude=targets.Longitude,... MinElevationAngle=30);
Define some quantities that are part of the satellite constellation definition. For details, see walkerDelta.
phasing = 0;
argLat = 15; % degOptimization Problem Definition
To formulate this problem as an optimization problem, define the optimization variables, and then define the constraints and objective function in terms of these variables. Use the Problem-Based Optimization Workflow (Optimization Toolbox), which provides an easy-to-use interface for setting up the optimization problem.
Optimization Variables
Use the following variables for the optimization problem:
numPlanes— Number of orbital planes, an integer from 1 through 10.satPerPlane— Number of satellites per orbital plane, an integer from 1 through 20.inclination— Inclination in degrees, a real scalar from 40 through 80.altitude— Altitude in megameters, a real scalar from 0.5 through 1.2. To make this variable have roughly the same scale as the other variables, use megameters instead of the more familiar kilometers or meters. Thealt2radiushelper function at the end of this example converts height from megameters to meters, and includes the radius of the Earth in the conversion.
Define the optimization variables using the optimvar function. Include the variable type (integer or continuous, where noted) and bounds.
numPlanes = optimvar("numPlanes",Type="integer",LowerBound=1,UpperBound=10); satPerPlane = optimvar("satPerPlane",Type="integer",LowerBound=1,UpperBound=20); inclination = optimvar("inclination",LowerBound=40,UpperBound=80); altitude = optimvar("altitude",LowerBound=0.5,UpperBound=1.2);
Objective Function
The objective is to minimize the number of satellites, which is the number of satellites per orbital plane times the number of orbital planes.
Create an optimization problem that includes this objective function for minimization.
satelliteProb = optimproblem(Objective=satPerPlane*numPlanes,ObjectiveSense="minimize");Constraints
The constraint for this problem is
Visibility is a complicated function of the variables. The observability helper function at the end of this example calculates this quantity. To place this helper function in the problem, convert the function to an optimization expression using the fcn2optimexpr function.
visibility = fcn2optimexpr(@observability,numPlanes,satPerPlane,mission,...
altitude,inclination,phasing,argLat);Add the constraint to the optimization problem.
satelliteProb.Constraints = visibility >= minObservability;
Review the problem.
show(satelliteProb)
OptimizationProblem :
Solve for:
altitude, inclination, numPlanes, satPerPlane
where:
numPlanes, satPerPlane integer
minimize :
satPerPlane*numPlanes
subject to :
arg_LHS >= arg_RHS
where:
arg1 = observability(numPlanes, satPerPlane, extraParams{1}, altitude, inclination, 0, 15);
arg_LHS = arg1;
arg2 = 0.9;
arg1 = arg2(ones(1,4));
arg_RHS = arg1(:);
extraParams
variable bounds:
0.5 <= altitude <= 1.2
40 <= inclination <= 80
1 <= numPlanes <= 10
1 <= satPerPlane <= 20
Solve Problem
The problem formulation is complete. Determine which solvers are available to solve the problem.
[default,available] = solvers(satelliteProb)
default = "ga"
available = 1×3 string
"ga" "surrogateopt" "gamultiobj"
For a time-consuming, integer-constrained problem such as this one, the surrogateopt solver is often more efficient than the default ga.
Solve the problem using the surrogateopt solver. To monitor the solution progress, specify the optimplotfvalconstr plot function. To try for a faster solution, specify parallel computing (requires Parallel Computing Toolbox™). To attempt to get a better surrogate model, set the MinSurrogatePoints option to 40, which is double the default value. Also, set the maximum number of function evaluations to 300, which is 100 more than the default value. When running in parallel, surrogateopt does not give reproducible results. So, in case your execution environment is serial, set the random seed for reproducible results.
rng default % For reproducibility options = optimoptions("surrogateopt",PlotFcn=@optimplotfvalconstr,... UseParallel=true,MaxFunctionEvaluations=300,MinSurrogatePoints=40); [sol,fval,exitflag,output] = solve(satelliteProb,Solver="surrogateopt",Options=options)
Solving problem using surrogateopt.
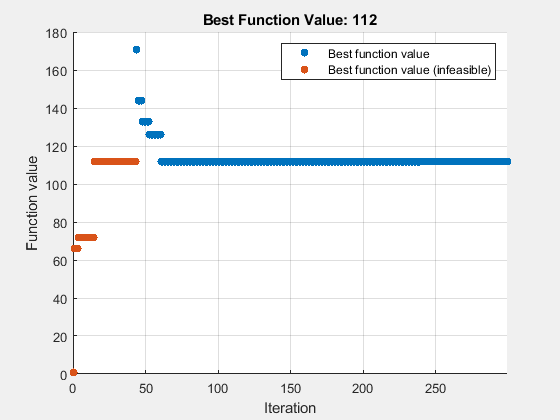
surrogateopt stopped because it exceeded the function evaluation limit set by 'options.MaxFunctionEvaluations'.
sol = struct with fields:
altitude: 1.2000
inclination: 62.8358
numPlanes: 7
satPerPlane: 16
fval = 112
exitflag =
SolverLimitExceeded
output = struct with fields:
elapsedtime: 4.9507e+03
funccount: 300
constrviolation: 3.4602e-04
ineq: [-0.1000 -0.1000 -0.1000 3.4602e-04]
rngstate: [1×1 struct]
message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'
solver: 'surrogateopt'
Display Solution
Obtain separate variables from the optimization solution.
numPlanes = sol.numPlanes
numPlanes = 7
numSatPerPlane = sol.satPerPlane
numSatPerPlane = 16
altitudeMm = sol.altitude
altitudeMm = 1.2000
inclination = sol.inclination
inclination = 62.8358
disp("Total number of satellites: " + evaluate(satelliteProb.Objective,sol))Total number of satellites: 112
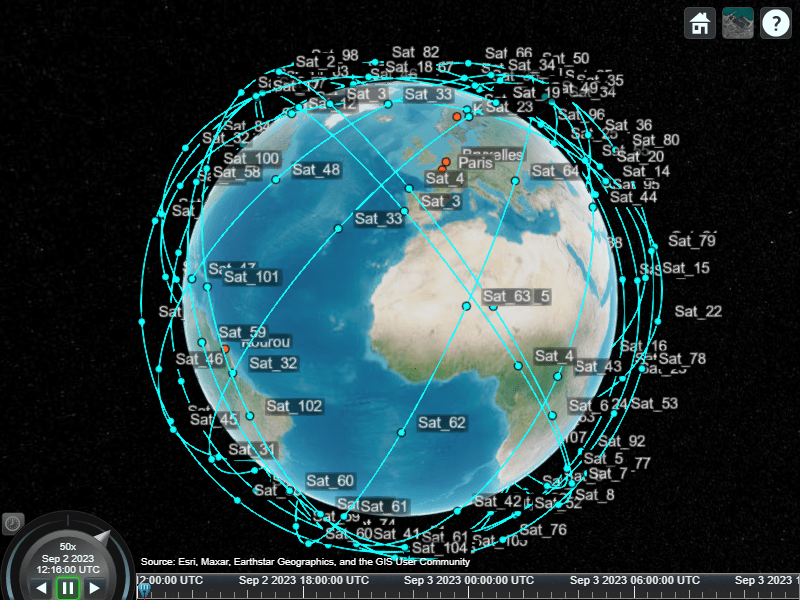
Visualize the satellite constellation.
radiusMeters = alt2radius(altitudeMm); mission.Constellation = walkerDelta(... mission.Scenario,... radiusMeters,... inclination,... numSatPerPlane*numPlanes,... numPlanes,... phasing,... ArgumentOfLatitude=argLat,... Name="Sat"); satelliteScenarioViewer(mission.Scenario);
Helper Functions
This code creates the alt2radius function.
function radiusMeters = alt2radius(altitude) % Convert altitude in Mm to radius in m. % Add the radius of the Earth in Mm. radius = altitude + 6.378137; % Convert the radius to meters. radiusMeters = radius * 1000 * 1000; end
This code creates the observability function.
function targetVisibilityPct = observability(numPlanes,satPerPlane,mission,... altitude,inclination,phasing,argLat) % The radius is in megameters (1000s of km) to keep the optimization search % bounded in [0.5 1.5], which is roughly low Earth orbit. % Convert the radius to meters for walkerDelta setup. radiusMeters = alt2radius(altitude); mission.Constellation = walkerDelta(... mission.Scenario,... radiusMeters,... inclination,... satPerPlane*numPlanes,... numPlanes,... phasing,... ArgumentOfLatitude=argLat,... Name="Sat"); % Compute the access for each target. targetVisibilityPct = zeros(numel(mission.Targets),1); for targetIdx = 1:numel(mission.Targets) accessAnalysis = access(mission.Constellation,mission.Targets(targetIdx)); satAccess = accessStatus(accessAnalysis); systemAccess = any(satAccess,1); targetVisibilityPct(targetIdx) = mean(systemAccess); end end