Wavelet Denoising
This example shows how to use wavelets to denoise signals and images. Because wavelets localize features in your data to different scales, you can preserve important signal or image features while removing noise. The basic idea behind wavelet denoising, or wavelet thresholding, is that the wavelet transform leads to a sparse representation for many real-world signals and images. What this means is that the wavelet transform concentrates signal and image features in a few large-magnitude wavelet coefficients. Wavelet coefficients which are small in value are typically noise and you can "shrink" those coefficients or remove them without affecting the signal or image quality. After you threshold the coefficients, you reconstruct the data using the inverse wavelet transform.
Denoise a Signal
To illustrate wavelet denoising, create a noisy "bumps" signal. In this case you have both the original signal and the noisy version.
rng default; [X,XN] = wnoise('bumps',10,sqrt(6)); subplot(211) plot(X); title('Original Signal'); AX = gca; AX.YLim = [0 12]; subplot(212) plot(XN); title('Noisy Signal'); AX = gca; AX.YLim = [0 12];
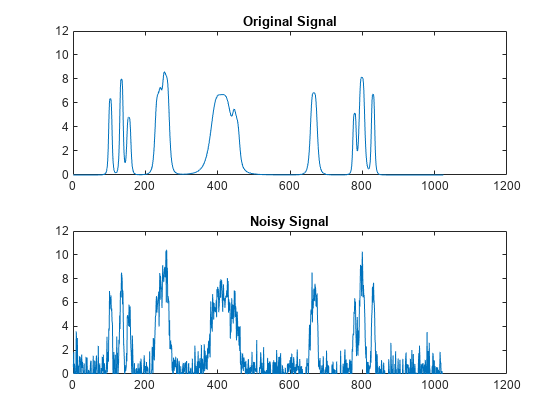
Denoise the signal down to level 4 using wdenoise with default settings. wdenoise uses the decimated wavelet transform. Plot the result along with the original signal.
xd = wdenoise(XN,4); figure; plot(X,'r') hold on; plot(xd) legend('Original Signal','Denoised Signal','Location','NorthEastOutside') axis tight; hold off;

You can also denoise the signal using the undecimated wavelet transform. Denoise the signal again down to level 4 using the undecimated wavelet transform. Plot the result along with the original signal.
xdMODWT = wden(XN,'modwtsqtwolog','s','mln',4,'sym4'); figure; plot(X,'r') hold on; plot(xdMODWT) legend('Original Signal','Denoised Signal','Location','NorthEastOutside') axis tight; hold off;

You see that in both cases, wavelet denoising has removed a considerable amount of the noise while preserving the sharp features in the signal. This is a challenge for Fourier-based denoising. In Fourier-based denoising, or filtering, you apply a lowpass filter to remove the noise. However, when the data has high-frequency features such as spikes in a signal or edges in an image, the lowpass filter smooths these out.
You can also use wavelets to denoise signals in which the noise is nonuniform. Import and examine a portion of a signal showing electricity consumption over time.
load leleccum; indx = 2000:3450; x = leleccum(indx); plot(x) grid on;
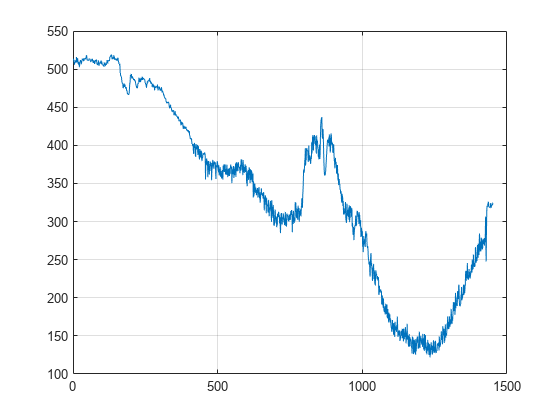
The signal appears to have more noise after approximately sample 500. Accordingly, you want to use different thresholding in the initial part of the signal. You can use cmddenoise to determine the optimal number of intervals to denoise and denoise the signal. In this example, use the 'db3' wavelet and decompose the data down to level 3.
[SIGDEN,~,thrParams,~,BestNbOfInt] = cmddenoise(x,'db3',3);Display the number of intervals and the sample values that delimit the intervals.
BestNbOfInt
BestNbOfInt = 2
thrParams{1}(:,1:2)ans = 2×2
1 412
412 1451
Two intervals were identified. The sample marking the boundary between the two segments is 412. If you plot the signal and mark the two signal segments, you see that the noise does appear different before and after sample 412.
plot(x) hold on; plot([412 412],[100 550],'r') hold off;

Plot the denoised signal.
plot(SIGDEN)
title('Denoised Signal')
Denoise an Image
You can also use wavelets to denoise images. In images, edges are places where the image brightness changes rapidly. Maintaining edges while denoising an image is critically important for perceptual quality. While traditional lowpass filtering removes noise, it often smooths edges and adversely affects image quality. Wavelets are able to remove noise while preserving the perceptually important features.
Load a noisy image. Denoise the image using wdenoise2 with default settings. By default, wdenoise2 uses the biorthogonal wavelet bior4.4. To display the original and denoised images, do not provide any output arguments.
load('jump.mat')
wdenoise2(jump)
Note that edges in the image are not smoothed out by the denoising process.