filterbank
Wavelet and scaling filters
Syntax
Description
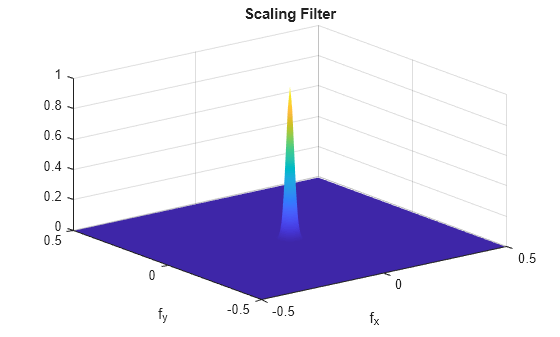
phif = filterbank(sf)sf. phif is a single or double-precision matrix
depending on the value of the Precision property of the scattering
network. phif has dimensions
M-by-N, where M and
N are the padded row and column sizes of the scattering network.
[
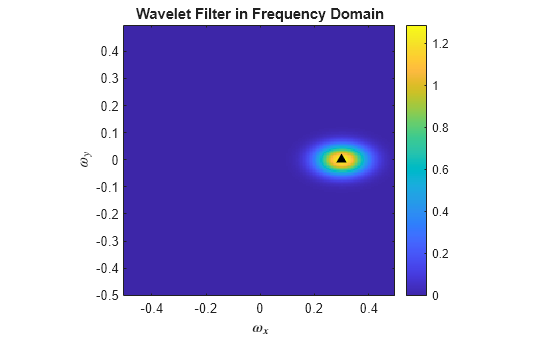
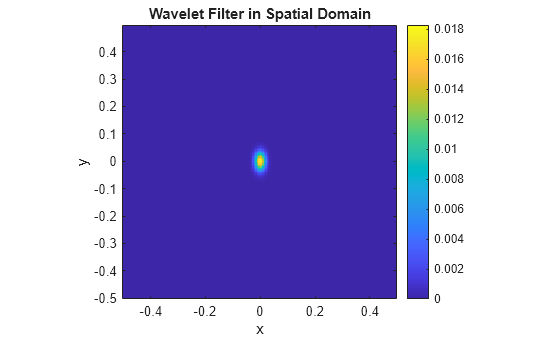
returns the Fourier transforms for the wavelet filters in phif,psifilters] = filterbank(sf)psifilters.
psifilters is an Nfb-by-1 cell array, where
Nfb is the number of filter banks in the scattering network. Each
element of psifilters is a 3-D array. The 3-D arrays are
M-by-N-by-L, where
M and N are the padded row and column sizes of the
wavelet filters and L is the number of wavelet filters for each filter
bank. The wavelet filters are ordered by increasing scale with
NumRotations wavelet filters for each scale. Within a scale, the
wavelet filters are ordered by rotation angle.
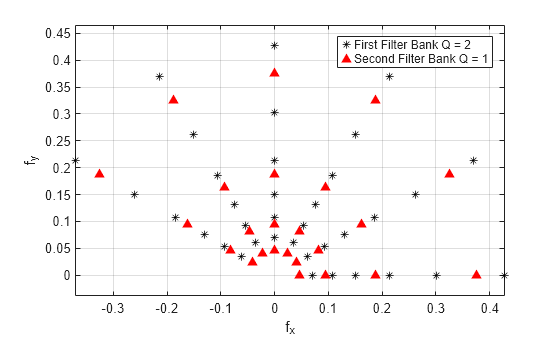
[
returns the center spatial frequencies for the wavelet filters in
phif,psifilters,f] = filterbank(sf)psifilters. f is an Nfb-by-1
cell array, where Nfb is the number of filter banks in
sf. The jth element of f
contains the center frequencies for the jth wavelet filter bank in
psifilters. Each element of f is a
L-by-2 matrix with each row containing the center frequencies of the
corresponding Lth wavelet.
[
returns the filter parameters for the 2-D scattering network.
phif,psifilters,f,filterparams] = filterbank(sf)filterparams is an Nfb-by-1 cell array of
MATLAB® tables, where the jth element of
filterparams is a MATLAB table containing the filter parameters for the jth filter
bank
[___] = filterbank(
returns the desired outputs for the filter banks specified in sf,fb)fb.
fb is a scalar or vector of integers between 1 and
numfilterbanks(sf) inclusive. If fb is a scalar,
psifilters is an
M-by-N-by-L matrix, and
filterparams is a MATLAB table.
Examples
Input Arguments
Output Arguments
More About
Version History
Introduced in R2019a