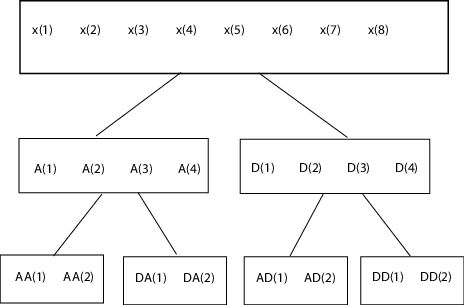
otnodes

Order terminal nodes of binary wavelet packet tree

Syntax

[Tn_Pal,Tn_Seq] = otnodes(WPT)

[Tn_Pal,Tn_Seq,I,J] = otnodes(WPT)

[DP_Pal,DP_Seq] = otnodes(WPT,'dp')

Description

[Tn_Pal,Tn_Seq] = otnodes(WPT) returns the terminal nodes of the binary wavelet packet tree, WPT, in Paley (natural) ordering, Tn_Pal, and sequency (frequency) ordering, Tn_Seq.

[Tn_Pal,Tn_Seq,I,J] = otnodes(WPT) returns the permutations of the terminal node indices such that Tn_Seq = Tn_Pal(I) and Tn_Pal = Tn_Seq(J).

[DP_Pal,DP_Seq] = otnodes(WPT,'dp') returns the Paley- and frequency-ordered terminal nodes in node depth-position format.

Examples

Order Terminal Nodes

Order terminal nodes with Paley and frequency ordering.

x = randn(8,1);
wpt = wpdec(x,2,'haar');
[Tn_Pal,Tn_Seq] = otnodes(wpt)

Tn_Pal = 4×1

     3
     4
     5
     6

Tn_Seq = 4×1

     3
     4
     6
     5

Return Permutations for Ordering

Return permutations for Paley and frequency ordering.

load noisdopp;
wpt = wpdec(noisdopp,6,'sym4');
[Tn_Pal,Tn_Seq,I,J] = otnodes(wpt);
isequal(Tn_Seq(J),Tn_Pal)

ans = logical
   1

isequal(Tn_Seq,Tn_Pal(I))

ans = logical
   1

Order Terminal Nodes by Depth and Position

Order terminal nodes by depth and position.

x = randn(8,1);
wpt = wpdec(x,2,'haar');
[DP_Pal,DP_Seq] = otnodes(wpt,'dp')

DP_Pal = 4×2

     2     0
     2     1
     2     2
     2     3

DP_Seq = 4×2

     2     0
     2     1
     2     3
     2     2

Order Terminal Nodes from Wavelet Packet Tree

Create a wavelet packet tree. Split some of the tree nodes, then plot the modified tree.

t = wptree(2,2,rand(1,512),"haar");
 t = wpsplt(t,4);
 t = wpsplt(t,5);
 t = wpsplt(t,10);
 plot(t)

In Node Label, select Index to get this figure:

Obtain the terminal nodes in Paley (natural) ordering and sequency (frequency) ordering.

 [tn_Pal,tn_Seq,I,J] = otnodes(t);
 [tn_Pal,tn_Seq,I,J]

ans = 7×4

     3     3     1     1
     9    21     3     4
    21    22     4     2
    22     9     2     3
    11     6     7     7
    12    12     6     6
     6    11     5     5

Input Arguments

WPT — Binary wavelet packet tree

wptree object

Binary wavelet packet tree, specified as a wptree object. You can use treeord to determine the order of your wavelet packet tree.

Output Arguments

Tn_Pal — Terminal nodes in Paley (natural) ordering

vector

Terminal nodes in Paley (natural) ordering, returned as a N-by-1 column vector, where N is the number of terminal nodes.

Tn_Seq — Terminal nodes in sequency ordering

vector

Terminal nodes in sequency ordering, returned as a N-by-1 column vector, where N is the number of terminal nodes.

I — Permutations of Paley-ordered terminal node indices

vector

Permutations of Paley-ordered terminal node indices, returned as a N-by-1 column vector, where N is the number of terminal nodes. The permutations are such that Tn_Seq = Tn_Pal(I).

J — Permutations of sequency-ordered terminal node indices

vector

Permutations of sequency-ordered terminal node indices, returned as a N-by-1 column vector, where N is the number of terminal nodes. The permutations are such that Tn_Pal = Tn_Seq(J).

DP_Pal — Paley-ordered terminal nodes in depth-position format

matrix

Paley-ordered terminal nodes in depth-position format, returned as a N-by-2 matrix, where N is the number of terminal nodes. The first column contains the depth index, and the second column contains the position index.

DP_Seq — Sequency-ordered terminal nodes in depth-position format

matrix

Sequency-ordered terminal nodes in depth-position format, returned as a N-by-2 matrix, where N is the number of terminal nodes. The first column contains the depth index, and the second column contains the position index.

More About

Paley (Natural) and Sequency (Frequency) Ordering

The discrete wavelet packet transform iterates on both approximation and detail coefficients at each level. In this transform, A denotes the lowpass (approximation) filter followed by downsampling. D denotes the highpass (detail) filter followed by downsampling. The figure represents a wavelet packet transform in Paley ordering acting on a time series of length 8. The transform has a depth of two.

Because of aliasing introduced by downsampling, the frequency content extracted by the operator AD is higher than the frequency content extracted by the DD operator. Therefore, the terminal nodes in frequency (sequency) order are: AA,DA,DD,AD. The terminal nodes in Paley order have the following indices: 3,4,5,6. The frequency order has the indices: 3,4,6,5.

References

[1] Wickerhauser, Mladen Victor. Lectures on Wavelet Packet Algorithms, Technical Report, Washington University, Department of Mathematics, 1992.

Version History

Introduced in R2010b