Main Content

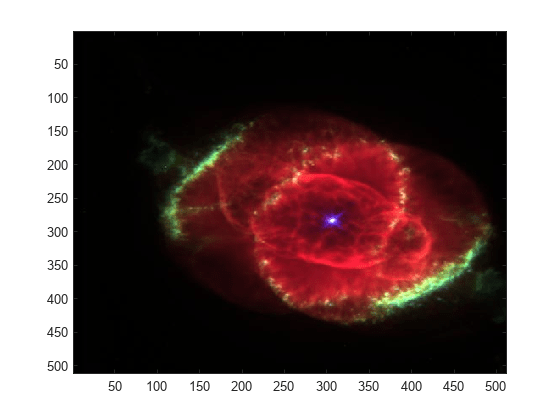
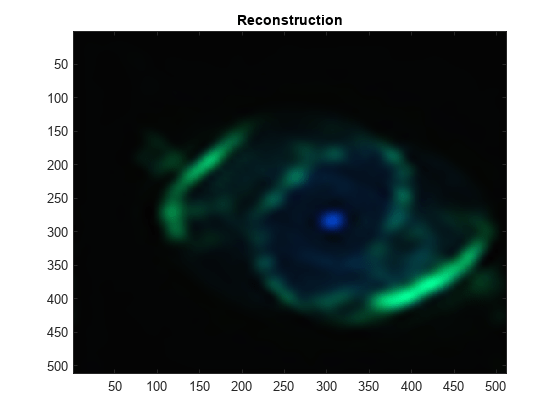
iswt2

Inverse discrete stationary 2-D wavelet transform

collapse all in page

    Syntax

    X = iswt2(swc,wname)
    X = iswt2(swc,LoR,HiR)
    X = iswt2(A,H,V,D,wname)
    X = iswt2(A,H,V,D,LoR,HiR)

    Description

    X = iswt2(swc,wname) returns the inverse discrete stationary 2-D wavelet transform of the wavelet decomposition swc using the wavelet wname. The decomposition swc is the output of swt2.

    Note

    swt2 uses double-precision arithmetic internally and returns double-precision coefficient matrices. swt2 warns if there is a loss of precision when converting to double.

    X = iswt2(swc,LoR,HiR) uses the specified lowpass and highpass wavelet reconstruction filters LoR and HiR, respectively.

    X = iswt2(A,H,V,D,wname) uses the approximation coefficients array A and detail coefficient arrays H, V, and D. The arrays H, V, and D contain the horizontal, vertical, and diagonal detail coefficients, respectively. The arrays are the output of swt2.

    • If the decomposition swc or the coefficient arrays A, H, V, and D were generated from a multilevel decomposition of a 2-D matrix, the syntax X = iswt2(A(:,:,end),H,V,D,wname) reconstructs the 2-D matrix.

    • If the decomposition swc or the coefficient arrays A, H, V, and D were generated from a single-level decomposition of a 3-D array, the syntax X = iswt2(A(:,:,1,:),H,V,D,wname) reconstructs the 3-D array.

    example

    X = iswt2(A,H,V,D,LoR,HiR) uses the lowpass and highpass wavelet reconstruction filters LoR and HiR, respectively.

    • If the decomposition swc or the coefficient arrays A, H, V, and D were generated from a multilevel decomposition of a 2-D matrix, the syntax X = iswt2(A(:,:,end),H,V,D,LoR,HiR) reconstructs the 2-D matrix.

    • If the decomposition swc or the coefficient arrays A, H, V, and D were generated from a single-level decomposition of a 3-D array, the syntax X = iswt2(A(:,:,1,:),H,V,D,LoR,HiR) reconstructs the 3-D array.

    example

    Examples

    collapse all

    Open Live Script

    Show perfect reconstruction using swt2 and iswt2 with an orthogonal wavelet.

    load woman
[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters('db6');
[ca,chd,cvd,cdd] = swt2(X,3,Lo_D,Hi_D);
recon = iswt2(ca,chd,cvd,cdd,Lo_R,Hi_R);
norm(X-recon)
    ans = 
1.0126e-08
    Open Live Script

    This example shows how to reconstruct an RGB image from a multilevel stationary wavelet decomposition using approximation and detail coefficient arrays.

    Load an RGB image. An RGB image is also referred to as a truecolor image. The image is a 3-D array of type uint8. Since swt2 requires that the first and second dimensions both be divisible by a power of 2, extract a portion of the image and view it.

    imdata = imread('ngc6543a.jpg');
x = imdata(1:512,1:512,:);
image(x)

    Figure contains an axes object. The axes object contains an object of type image.

    Obtain the level 4 stationary wavelet decomposition of the image using the db4 wavelet. Return the approximation coefficients and horizontal, vertical, and detail coefficients as separate arrays.

    [a,h,v,d] = swt2(x,4,'db4');

    Reconstruct an image using the green and blue components of the approximation coefficients. Display the reconstruction.

    a2 = zeros(size(a));
a2(:,:,2:3,4)=a(:,:,2:3,4);
xrec = iswt2(a2,0*h,0*v,0*d,'db4');
xrec2 = (xrec-min(xrec(:)))/(max(xrec(:))-min(xrec(:)));
image(xrec2)
title('Reconstruction')

    Figure contains an axes object. The axes object with title Reconstruction contains an object of type image.

    Input Arguments

    collapse all

    Stationary wavelet decomposition, specified as a 3-D or 4-D array. The decomposition contains the approximation and detail coefficients of the 2-D stationary wavelet transform (SWT). The stationary wavelet decomposition is the output of swt2.

    Data Types: double

    Analyzing wavelet, specified as a character vector or string scalar. iswt2 supports only Type 1 (orthogonal) or Type 2 (biorthogonal) wavelets. See wfilters for a list of orthogonal and biorthogonal wavelets. The specified wavelet must be the same wavelet used to obtain the approximation and detail coefficients.

    Wavelet reconstruction filters, specified as a pair of even-length real-valued vectors. LoR is the lowpass reconstruction filter, and HiR is the highpass reconstruction filter. The lengths of LoR and HiR must be equal. See wfilters for additional information.

    Approximation coefficients, specified as a multidimensional array. The array is the output of swt2.

    Data Types: double

    Detail coefficients, specified as multidimensional arrays of equal size. H, V, and D contain the horizontal, vertical, and diagonal detail coefficients, respectively. The arrays are the output of swt2.

    Data Types: double

    Output Arguments

    collapse all

    Reconstruction, returned as a 2-D matrix or 3-D array.

    If swc or (A,H,V,D) are obtained from an indexed image analysis or a truecolor (RGB) image analysis, then X is an m-by-n matrix or an m-by-n-by-3 array, respectively.

    References

    [1] Nason, G. P., and B. W. Silverman. “The Stationary Wavelet Transform and Some Statistical Applications.” In Wavelets and Statistics, edited by Anestis Antoniadis and Georges Oppenheim, 103:281–99. New York, NY: Springer New York, 1995. https://doi.org/10.1007/978-1-4612-2544-7_17.

    [2] Coifman, R. R., and D. L. Donoho. “Translation-Invariant De-Noising.” In Wavelets and Statistics, edited by Anestis Antoniadis and Georges Oppenheim, 103:125–50. New York, NY: Springer New York, 1995. https://doi.org/10.1007/978-1-4612-2544-7_9.

    [3] Pesquet, J.-C., H. Krim, and H. Carfantan. “Time-Invariant Orthonormal Wavelet Representations.” IEEE Transactions on Signal Processing 44, no. 8 (August 1996): 1964–70. https://doi.org/10.1109/78.533717.

    Extended Capabilities

    Version History

    Introduced before R2006a

    expand all

    See Also

    | |