dwpt

Wavelet packet 1-D transform

Since R2020a

Syntax

wpt = dwpt(X)

wpt = dwpt(X,wname)

wpt = dwpt(X,LoD,HiD)

[wpt,l] = dwpt(___)

[wpt,l,packetlevels] = dwpt(___)

[wpt,l,packetlevels,f] = dwpt(___)

[wpt,l,packetlevels,f,re] = dwpt(___)

[___] = dwpt(___,Name=Value)

Description

wpt = dwpt(X) returns the terminal (final-level) nodes of the discrete wavelet packet transform (DWPT) of X. The input X is a vector, matrix, or timetable. By default, the fk18 wavelet is used, and the decomposition level is floor(log2(Ns)), where Ns is the number of data samples. The wavelet packet transform wpt is a 1-by-N cell array, where N = 2^floor(log2(Ns)).

wpt = dwpt(X,wname) uses the wavelet specified by wname for the DWPT. wname must be recognized by wavemngr.

wpt = dwpt(X,LoD,HiD) uses the scaling (lowpass) filter, LoD, and wavelet (highpass) filter, HiD.

[wpt,l] = dwpt(___) also returns the bookkeeping vector using any of the previous syntaxes. The vector l contains the length of the input signal and the number of coefficients by level. The bookkeeping vector is required for perfect reconstruction.

[wpt,l,packetlevels] = dwpt(___) also returns the transform levels of the nodes of wpt using any of the previous syntaxes.

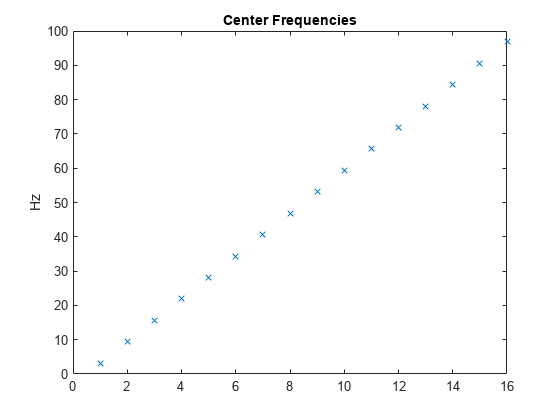
[wpt,l,packetlevels,f] = dwpt(___) also returns the center frequencies of the approximate passbands in cycles per sample using any of the previous syntaxes.

[wpt,l,packetlevels,f,re] = dwpt(___) also returns the relative energy for the wavelet packets in wpt using any of the previous syntaxes. The relative energy is the proportion of energy contained in each wavelet packet by level.

[___] = dwpt(___,Name=Value) specifies options using name-value pair arguments in addition to the input arguments in the previous syntaxes. For example, Level=4 specifies the decomposition level.

Examples

Multichannel Discrete Wavelet Packet Transform

Load the 23-channel EEG data Espiga3 [3]. The data is sampled at 200 Hz.

load Espiga3

Compute the 1-D DWPT of the data using the sym3 wavelet down to level 4. Obtain the terminal wavelet packet nodes, bookkeeping vector, and center frequencies of the approximate passbands.

[wpt,bk,~,f] = dwpt(Espiga3,"sym3",Level=4);

The output wpt is a 1-by-$$2^4$$ cell array. Every element of wpt is a matrix. Choose any terminal node, and confirm the size of the matrix is 23-by-M, where M is the last element of the bookkeeping vector bk.

nd = 13;
size(wpt{nd})

ans = 1×2

    23    66

bk(end)

ans = 
66

Extract the final-level coefficients of the fifth channel.

p5 = cell2mat(cellfun(@(x) x(5,:).',wpt,UniformOutput=false));
size(p5)

ans = 1×2

    66    16

The terminal nodes are sequency-ordered. Plot the center frequencies of the approximate passbands in hertz, and confirm they are in order of increasing frequency.

plot(200*f,"x")
title("Center Frequencies")
ylabel("Hz")

Input Arguments

X — Input data

vector | matrix | timetable

Input data, specified as a vector, matrix, or timetable. If X is a matrix, the transform is applied to each column of X. If X is a timetable, X must either contain a matrix in a single variable or column vectors in separate variables. X must be uniformly sampled.

Data Types: single | double
Complex Number Support: Yes

wname — Wavelet

"fk18" (default) | character vector | string scalar

Wavelet to use in the DWPT, specified as a character vector or string scalar. wname must be recognized by wavemngr.

You cannot specify both wname and a filter pair, LoD and HiD.

Example: wpt = dwpt(data,"sym4") specifies the sym4 wavelet.

LoD,HiD — Wavelet analysis filters

real-valued vectors

Wavelet analysis (decomposition) filters to use in the DWPT, specified as a pair of real-valued vectors. LoD is the scaling (lowpass) analysis filter, and HiD is the wavelet (highpass) analysis filter. You cannot specify both wname and a filter pair, LoD and HiD. See wfilters for additional information.

Note

dwpt does not check that LoD and HiD satisfy the requirements for a perfect reconstruction wavelet packet filter bank. To confirm your filter pair satisfies the requirements, use isorthwfb or isbiorthwfb.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: wpt = dwpt(x,"sym4",Level=4) specifies a level 4 decomposition using the sym4 wavelet.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: wpt = dwpt(x,"sym4","Level",4) specifies a level 4 decomposition using the sym4 wavelet.

Level — Wavelet decomposition level

floor(log2(Ns)) (default) | positive integer

Wavelet decomposition level, specified as a positive integer less than or equal to floor(log2(Ns)), where Ns is the number of samples in the data. If unspecified, Level defaults to floor(log2(Ns)).

FullTree — Wavelet packet tree handling

false or 0 (default) | true or 1

Wavelet packet tree handling, specified as a numeric or logical 1 (true) or 0 (false). When set to true, wpt contains the full packet tree. When set to false, wpt contains only the terminal nodes. If unspecified, FullTree defaults to false.

Boundary — Wavelet packet transform boundary handling

"reflection" (default) | "periodic"

Wavelet packet transform boundary handling, specified as "reflection" or "periodic". Setting to "reflection" or "periodic", the wavelet packet coefficients are extended at each level based on the "sym" or "per" mode in dwtmode, respectively. If unspecified, Boundary defaults to "reflection".

Output Arguments

wpt — Wavelet packet transform

cell array

Wavelet packet transform, returned as a 1-by-M cell array. If taking the DWPT of one signal, each element of wpt is a vector. Otherwise, each element is a matrix. The coefficients in the jth row of the matrix correspond to the signal in the jth column of X. The packets are sequency-ordered.

If returning the terminal nodes of a level N decomposition, wpt is a 1-by-2^N cell array. If returning the full wavelet packet tree, wpt is a 1-by-(2^N+1−2) cell array.

l — Bookkeeping vector

vector of positive integers

Bookkeeping vector, returned as a vector of positive integers. The vector l contains the length of the input signal and the number of coefficients by level and is required for perfect reconstruction.

packetlevels — Transform levels

vector of positive integers

Transform levels, returned as a vector of positive integers. The ith element of packetlevels corresponds to the ith element of wpt. If wpt contains only the terminal nodes, packetlevels is a vector with each element equal to the terminal level. If wpt contains the full wavelet packet tree, then packetlevels is a vector with 2^j elements for each level j.

f — Center frequencies

real-valued vector

Center frequencies of the approximate passbands in cycles per sample, returned as a real-valued vector. The jth element of f corresponds to the jth wavelet packet node of wpt. You can multiply the elements in f by a sampling frequency to convert to cycles per unit time.

re — Relative energy

cell array

Relative energy for the wavelet packets in wpt, returned as a cell array. The relative energy is the proportion of energy contained in each wavelet packet by level. The jth element of re corresponds to the jth wavelet packet node of wpt.

Each element of re is a scalar when taking the DWPT of one signal. Otherwise, when taking the DWPT of M signals, each element of re is a M-by-1 vector, where the ith element is the relative energy of the ith signal channel. For each channel, the sum of relative energies in the wavelet packets at a given level is equal to 1.

More About

Wavelet Packet Decomposition

The wavelet packet method is a generalization of wavelet decomposition that offers a richer signal analysis. Wavelet packet atoms are waveforms indexed by three naturally interpreted parameters: position and scale as in wavelet decomposition, and frequency.

For a given orthogonal wavelet function, a library of wavelet packets bases is generated. Each of these bases offers a particular way of coding signals, preserving global energy and reconstructing exact features. The wavelet packets can then be used for numerous expansions of a given signal.

Simple and efficient algorithms exist for both wavelet packets decomposition and optimal decomposition selection. Adaptive filtering algorithms with direct applications in optimal signal coding and data compression can then be produced.

In the orthogonal wavelet decomposition procedure, the generic step splits the approximation coefficients into two parts. After splitting we obtain a vector of approximation coefficients and a vector of detail coefficients, both at a coarser scale. The information lost between two successive approximations is captured in the detail coefficients. The next step consists in splitting the new approximation coefficient vector; successive details are never re-analyzed.

In the corresponding wavelet packets situation, each detail coefficient vector is also decomposed into two parts using the same approach as in approximation vector splitting. This offers the richest analysis: the complete binary tree is produced in the one-dimensional case or a quaternary tree in the two-dimensional case.

Algorithms

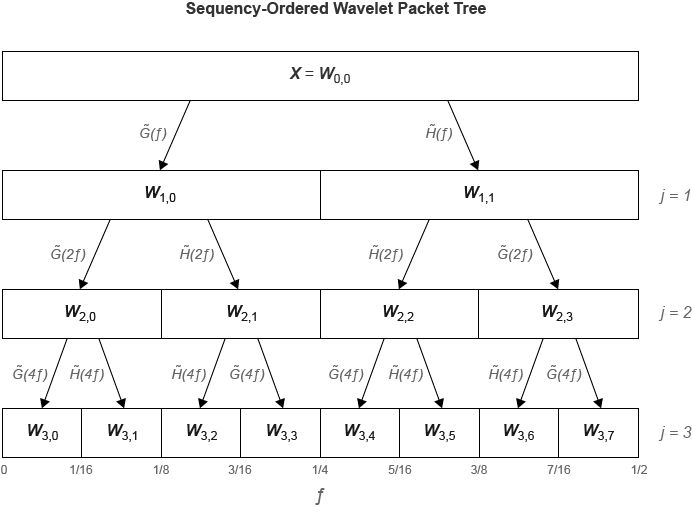
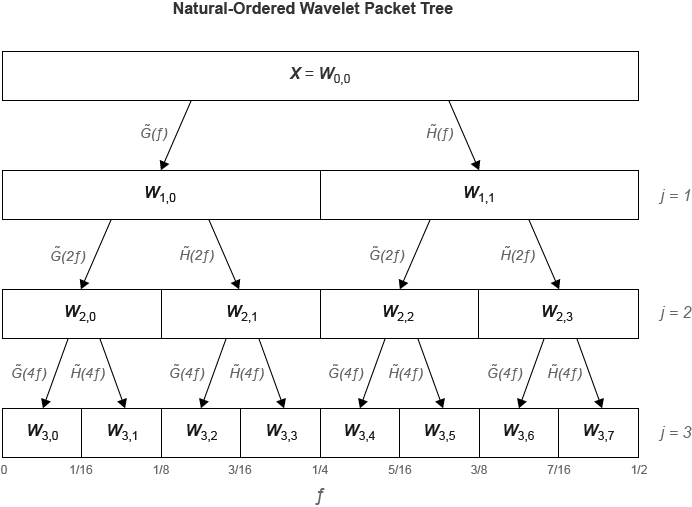
The dwpt function performs a discrete wavelet packet transform and produces a sequency-ordered wavelet packet tree. Compare the sequency-ordered and normal (Paley)-ordered trees. $$\tilde{G}(f)$$ is the scaling (lowpass) analysis filter, and $$\tilde{H}(f)$$ represents the wavelet (highpass) analysis filter. The labels at the bottom show the partition of the frequency axis [0, ½].

References

[1] Wickerhauser, Mladen Victor. Adapted Wavelet Analysis from Theory to Software. Wellesley, MA: A.K. Peters, 1994.

[2] Percival, D. B., and A. T. Walden. Wavelet Methods for Time Series Analysis. Cambridge, UK: Cambridge University Press, 2000.

[3] Mesa, Hector. “Adapted Wavelets for Pattern Detection.” In Progress in Pattern Recognition, Image Analysis and Applications, edited by Alberto Sanfeliu and Manuel Lazo Cortés, 3773:933–44. Berlin, Heidelberg: Springer Berlin Heidelberg, 2005. https://doi.org/10.1007/11578079_96.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• Timetable input data is not supported.

• The input wname must be constant.

Version History

Introduced in R2020a

R2023b: Compute DWPT of complex-valued data

The dwpt function supports complex-valued data.