ransac
Fit model to noisy data
Syntax
Description
[
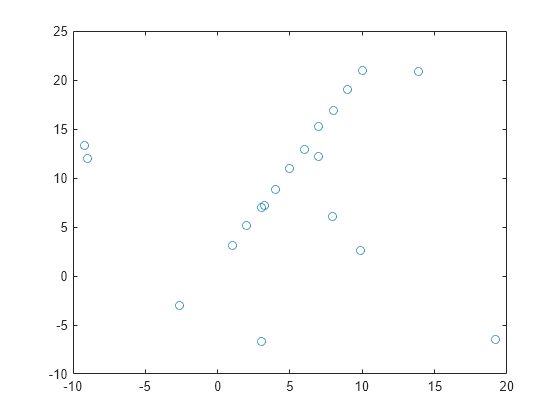
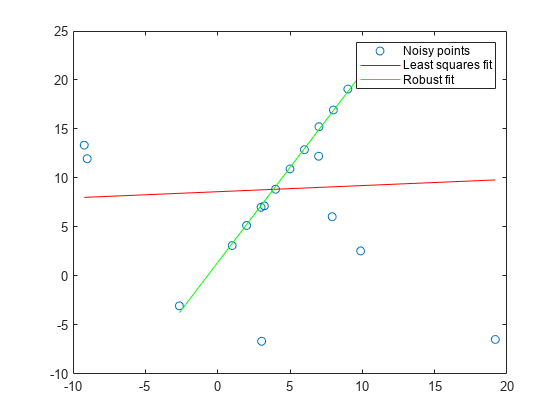
fits a model to noisy data using the M-estimator sample consensus (MSAC) algorithm,
a version of the random sample consensus (RANSAC) algorithm.model,inlierIdx]
= ransac(data,fitFcn,distFcn,sampleSize,maxDistance)
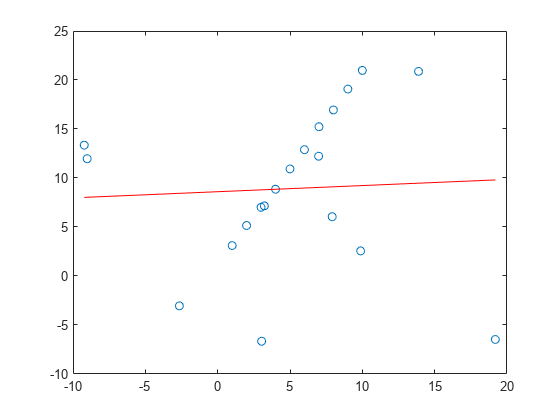
Specify your function for fitting a model, fitFcn, and your
function for calculating distances from the model to your data,
distFcn. The ransac function takes
random samples from your data using
sampleSize and uses the fit function to maximize the number
of inliers within maxDistance.
[___] = ransac(___,
additionally specifies one or more Name,Value)Name,Value pair
arguments.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
References
[1] Torr, P. H. S., and A. Zisserman. "MLESAC: A New Robust Estimator with Application to Estimating Image Geometry." Computer Vision and Image Understanding. Vol. 18, Issue 1, April 2000, pp. 138–156.
Extended Capabilities
Version History
Introduced in R2017a