Longitudinal Wheel
Longitudinal wheel with disc, drum, or mapped brake
Libraries:
Powertrain Blockset /
Drivetrain /
Wheels
Vehicle Dynamics Blockset /
Wheels and Tires
Description
The Longitudinal Wheel block implements the longitudinal behavior of an ideal wheel. You can specify the longitudinal force and rolling resistance calculation method, and brake type. Use the block in driveline and longitudinal vehicle simulations where low frequency tire-road and braking forces are required to determine vehicle acceleration, braking, and wheel-rolling resistance. For example, you can use the block to determine the torque and power requirements for a specified drive cycle or braking event. The block is not suitable for applications that require combined lateral slip.
There are four types of Longitudinal Wheel blocks. Each block implements a different brake type.
| Block Name | Brake Type Setting | Brake Implementation |
|---|---|---|
| Longitudinal Wheel - No Brake |
|
None |
| Longitudinal Wheel - Disc Brake |
|
Brake that converts the brake cylinder pressure into a braking force. |
| Longitudinal Wheel - Drum Brake |
|
Simplex drum brake that converts the applied force and brake geometry into a net braking torque. |
| Longitudinal Wheel - Mapped Brake |
|
Lookup table that is a function of the wheel speed and applied brake pressure. |
The block models longitudinal force as a function of wheel slip relative to the road surface. To calculate the longitudinal force, specify one of these Longitudinal Force parameters.
| Setting | Block Implementation |
|---|---|
|
|
Magic Formula with constant coefficient for stiffness, shape, peak, and curvature. |
|
|
Magic Formula with load-dependent coefficients that implement equations 4.E9 through 4.E18 in Tire and Vehicle Dynamics. |
|
|
Lookup table that is a function of the normal force and wheel slip ratio. |
To calculate the rolling resistance torque, specify one of these Rolling Resistance parameters.
| Setting | Block Implementation |
|---|---|
| None |
| Method in Stepwise Coastdown Methodology for Measuring Tire Rolling Resistance. The rolling resistance is a function of tire pressure, normal force, and velocity. |
| Method specified in ISO 28580:2018, Passenger car, truck and bus tyre rolling resistance measurement method — Single point test and correlation of measurement results. |
| Magic formula equations from 4.E70 in Tire and Vehicle Dynamics. The magic formula is an empirical equation based on fitting coefficients. |
| Lookup table that is a function of the normal force and spin axis longitudinal velocity. |
To calculate vertical motion, specify one of these Vertical Motion parameters.
| Setting | Block Implementation |
|---|---|
| Block passes the applied chassis forces directly through to the rolling resistance and longitudinal force calculations. |
| Vertical motion depends on wheel stiffness and damping. Stiffness is a function of tire sidewall displacement and pressure. Damping is a function of tire sidewall velocity and pressure. |
| The block uses the defined sidewall deflection directly in the effective radius calculation. |
Rotational Wheel Dynamics
The block calculates the inertial response of the wheel subject to:
Axle losses
Brake and drive torque
Tire rolling resistance
Ground contact through the tire-road interface
The input torque is the summation of the applied axle torque, braking torque, and moment arising from the combined tire torque.
For the moment arising from the combined tire torque, the block implements tractive wheel forces and rolling resistance with first order dynamics. The rolling resistance has a time constant parameterized in terms of a relaxation length.
To calculate the rolling resistance torque, you can specify one of these Rolling Resistance parameters.
| Setting | Block Implementation |
|---|---|
| Block sets rolling resistance,
|
| Block uses the method in SAE Stepwise Coastdown Methodology for Measuring Tire Rolling Resistance. The rolling resistance is a function of tire pressure, normal force, and velocity, specifically: |
| Block uses the method specified in ISO 28580:2018, Passenger car, truck and bus tyre rolling resistance measurement method — Single point test and correlation of measurement results. The method accounts for normal load, parasitic loss, and thermal corrections from test conditions, specifically: |
| Block calculates the rolling resistance,
|
| For the rolling resistance,
|
If the brakes are enabled, the block determines the braking locked or unlocked condition based on an idealized dry clutch friction model. Based on the lock-up condition, the block implements these friction and dynamic models.
| If | Lock-Up Condition | Friction Model | Dynamic Model |
|---|---|---|---|
Unlocked | |||
Locked |
The equations use these variables.
| ω | Wheel angular velocity |
| a | Velocity-independent force component |
| b | Linear velocity force component |
| c | Quadratic velocity force component |
| Le | Tire relaxation length |
| J | Moment of inertia |
| My | Rolling resistance torque |
| Ta | Applied axle torque |
| Tb | Braking torque |
| Td | Combined tire torque |
| Tf | Frictional torque |
| Ti | Net input torque |
| Tk | Kinetic frictional torque |
| To | Net output torque |
| Ts | Static frictional torque |
| Fc | Applied clutch force |
| Fx | Longitudinal force developed by the tire road interface due to slip |
| Reff | Effective clutch radius |
| Ro | Annular disc outer radius |
| Ri | Annular disc inner radius |
| Re | Effective tire radius while under load and for a given pressure |
| Vx | Longitudinal axle velocity |
| Fz | Vehicle normal force |
| Cr | Rolling resistance constant |
| Tamb | Ambient temperature |
| Tmeas | Measured temperature for rolling resistance constant |
| Fpl | Parasitic force loss |
| Kt | Thermal correction factor |
| ɑ | Tire pressure exponent |
| β | Normal force exponent |
| pi | Tire pressure |
| μs | Coefficient of static friction |
| μk | Coefficient of kinetic friction |
Brakes
If you specify the Brake Type parameter as
Disc, the block implements a disc brake. This figure
shows the side and front views of a disc brake.
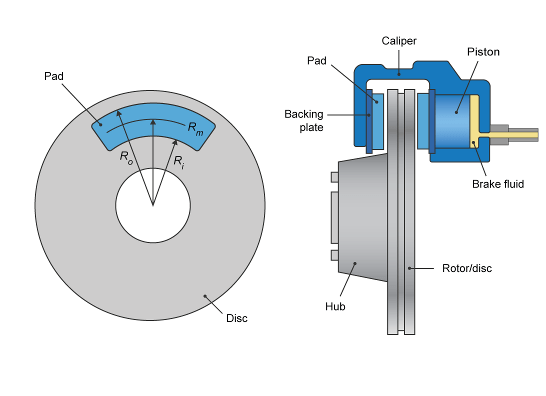
A disc brake converts brake cylinder pressure from the brake cylinder into force. The disc brake applies the force at the brake pad mean radius.
The block uses these equations to calculate brake torque for the disc brake.
The equations use these variables.
| Variable | Value |
|---|---|
| T | Brake torque |
| P | Applied brake pressure |
| N | Wheel speed |
| Npads | Number of brake pads in disc brake assembly |
| μstatic | Disc pad-rotor coefficient of static friction |
| μ | Disc pad-rotor coefficient of kinetic friction |
| Ba | Brake actuator bore diameter |
| Rm | Mean radius of brake pad force application on brake rotor |
| Ro | Outer radius of brake pad |
| Ri | Inner radius of brake pad |
If you specify the Brake Type parameter as
Drum, the block implements a static (steady-state)
simplex drum brake. A simplex drum brake consists of a single two-sided hydraulic
actuator and two brake shoes. The brake shoes do not share a common hinge pin.
The simplex drum brake model uses the applied force and brake geometry to calculate a net torque for each brake shoe. The drum model assumes that the actuators and shoe geometry are symmetrical for both sides, allowing a single set of geometry and friction parameters to be used for both shoes.
The block implements equations that are derived from these equations in Fundamentals of Machine Elements.
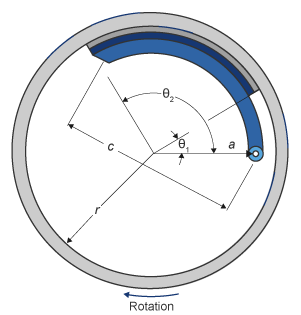
The equations use these variables.
| Variable | Value |
|---|---|
| T | Brake torque |
| P | Applied brake pressure |
| N | Wheel speed |
| μstatic | Disc pad-rotor coefficient of static friction |
| μ | Disc pad-rotor coefficient of kinetic friction |
| Trshoe | Right shoe brake torque |
| Tlshoe | Left shoe brake torque |
| a | Distance from drum center to shoe hinge pin center |
| c | Distance from shoe hinge pin center to brake actuator connection on brake shoe |
| r | Drum internal radius |
| Ba | Brake actuator bore diameter |
| Θ1 | Angle from shoe hinge pin center to start of brake pad material on shoe |
| Θ2 | Angle from shoe hinge pin center to end of brake pad material on shoe |
If you specify the Brake Type parameter as
Mapped, the block uses a lookup table to determine the
brake torque.
The equations use these variables.
| Variable | Value |
|---|---|
| T | Brake torque |
Brake torque lookup table | |
| P | Applied brake pressure |
| N | Wheel speed |
| μstatic | Friction coefficient of drum pad-face interface under static conditions |
| μ | Friction coefficient of disc pad-rotor interface |
The lookup table for the brake torque, , is a function of applied brake pressure and wheel speed, where:
T is brake torque, in N·m.
P is applied brake pressure, in bar.
N is wheel speed, in rpm.

Longitudinal Force
To model the Longitudinal Wheel block longitudinal forces, you can use the Magic Formula. The model provides a steady-state tire characteristic function Fx = f(κ, Fz), the longitudinal force Fx on the tire, based on:
Vertical load Fz
Wheel slip κ
The Magic Formula model uses these variables.
| Ω | Wheel angular velocity |
| rw | Wheel radius |
| Vx | Wheel hub longitudinal velocity |
| rwΩ | Tire tread longitudinal velocity |
| Vsx = rwΩ – Vx | Wheel slip velocity |
| κ = Vsx/|Vx| | Wheel slip |
| Fz, Fz0 | Vertical load and nominal vertical load on tire |
| Fx = f(κ, Fz) | Longitudinal force exerted on the tire at the contact point. Also a characteristic function f of the tire. |
If you set Longitudinal Force to Magic
Formula constant value, the block implements the Magic Formula
as a specific form of the tire characteristic function, characterized by four
dimensionless coefficients (B, C,
D, E), or stiffness, shape, peak, and curvature:
The slope of f at κ = 0 is BCD·Fz.
The coefficients are based on empirical tire data. These values are typical sets of constant Magic Formula coefficients for common road conditions.
| Surface | B | C | D | E |
|---|---|---|---|---|
| Dry tarmac | 10 | 1.9 | 1 | 0.97 |
| Wet tarmac | 12 | 2.3 | 0.82 | 1 |
| Snow | 5 | 2 | 0.3 | 1 |
| Ice | 4 | 2 | 0.1 | 1 |
If you set Longitudinal Force to Magic
Formula pure longitudinal slip, the block implements a more
general Magic Formula using dimensionless coefficients that are functions of the
tire load. The block implements the longitudinal force equations in Chapter 4 of
Tire and Vehicle Dynamics, including 4.E9 through 4.E18:
SHx and SVx represent offsets to the slip and longitudinal force in the force-slip function, or horizontal and vertical offsets if the function is plotted as a curve. μx is the longitudinal load-dependent friction coefficient. εx is a small number inserted to prevent division by zero as Fz approaches zero.
Vertical Dynamics
If you select no vertical degrees-of-freedom by setting Vertical
Motion to None, the block passes the
applied chassis forces directly through to the rolling resistance and longitudinal
force calculations.
If you set Vertical Motion to Mapped stiffness
and damping, the vertical motion depends on wheel stiffness and
damping. Stiffness is a function of tire sidewall displacement and pressure. Damping
is a function of tire sidewall velocity and pressure.
The block determines the vertical response using this differential equation.
When you disable the vertical degree-of-freedom, the input normal force from the vehicle passes directly to the longitudinal and rolling force calculations.
The block uses the wheel-fixed frame to resolve the vertical forces.

The equations use these variables.
| Fztire | Tire normal force along the wheel-fixed z-axis |
| m | Axle mass |
| Fzk | Tire normal force due to wheel stiffness along the wheel-fixed z-axis |
| Fzb | Tire normal force due to wheel damping along the wheel-fixed z-axis |
| Fz | Suspension or vehicle normal force along the wheel-fixed z-axis |
| PTire | Tire pressure |
Tire displacement, velocity, and acceleration, respectively, along the wheel-fixed z-axis |
Power Accounting
For the power accounting, the block implements these equations.
| Bus Signal | Description | Equations | ||
|---|---|---|---|---|
|
|
| Tractive power applied from the axle | |
| External torque applied by the axle to the wheel | |||
| Vertical force applied to the wheel by the vehicle or suspension | |||
|
|
| Tractive power loss | ||
| Rolling resistance power | |||
| Braking power | |||
| Rolling viscous damping loss | |||
| Vertical damping power | |||
|
|
| Rate of change of vertical kinetic energy | ||
| Rate of change of rotational kinetic energy | |||
| Rate of change of stored sidewall potential energy | |||
| Rate of change of gravitational potential energy | |||
The equations use these variables.
| ω | Wheel angular velocity |
| b | Linear velocity force component |
| Fx | Longitudinal force developed by the tire road interface due to slip |
| Fcp | Tire slip force at contact patch |
| Fz | Vehicle normal force |
| Fzb | Tire normal force due to wheel damping |
| Fzk | Tire normal force due to wheel stiffness |
| Iyy | Wheel rotational inertia |
| Mbrk | Braking moment |
| My | Rolling resistance torque |
| Re | Effective tire radius while under load and for a given pressure |
| T | Axle torque applied on wheel |
| Vx | Longitudinal axle velocity |
Tire displacement, velocity, and acceleration, respectively | |
| ω | Wheel angular velocity |
Vehicle vertical velocity along the vehicle-fixed z-axis |
Ports
Input
Output
Parameters
References
[1] Highway Tire Committee. Stepwise Coastdown Methodology for Measuring Tire Rolling Resistance. Standard J2452_199906. Warrendale, PA: SAE International, June 1999.
[2] Pacejka, H. B. Tire and Vehicle Dynamics. 3rd ed. Oxford, United Kingdom: SAE and Butterworth-Heinemann, 2012.
[3] Schmid, Steven R., Bernard J. Hamrock, and Bo O. Jacobson. "Chapter 18: Brakes and Clutches." Fundamentals of Machine Elements, SI Version. 3rd ed. Boca Raton, FL: CRC Press, 2014.
[4] Shigley, Joseph E., and Larry Mitchel. Mechanical Engineering Design. 4th ed. New York, NY: McGraw Hill, 1983.
[5] ISO 28580:2018. Passenger car, truck and bus tyre rolling resistance measurement method -- Single point test and correlation of measurement results. ISO (International Organization for Standardization), 2018.
Extended Capabilities
Version History
Introduced in R2017a
