harmonic

Harmonic function (harmonic number)

Syntax

harmonic(x)

Description

harmonic(x) returns the harmonic function of x. For integer values of x, harmonic(x) generates harmonic numbers.

Examples

Generate Harmonic Numbers

Generate the first 10 harmonic numbers.

harmonic(sym(1:10))

ans =
[ 1, 3/2, 11/6, 25/12, 137/60, 49/20, 363/140, 761/280, 7129/2520, 7381/2520]

Harmonic Function for Numeric and Symbolic Arguments

Find the harmonic function for these numbers. Since these are not symbolic objects, you get floating-point results.

harmonic([2 i 13/3])

ans =
   1.5000 + 0.0000i   0.6719 + 1.0767i   2.1545 + 0.0000i

Find the harmonic function symbolically by converting the numbers to symbolic objects.

y = harmonic(sym([2 i 13/3]))

y =
[ 3/2, harmonic(1i), 8571/1820 - (pi*3^(1/2))/6 - (3*log(3))/2]

If the denominator of x is 2, 3, 4, or 6, and |x| < 500, then the result is expressed in terms of pi and log.

Use vpa to approximate the results obtained.

vpa(y)

ans =
[ 1.5, 0.67186598552400983787839057280431...
 + 1.07667404746858117413405079475i,...
 2.1545225442213858782694336751358]

For |x| > 1000, harmonic returns the function call as it is. Use vpa to force harmonic to evaluate the function call.

harmonic(sym(1001))
vpa(harmonic(sym(1001)))

ans =
harmonic(1001)
ans =
7.4864698615493459116575172053329

Harmonic Function for Special Values

Find the harmonic function for special values.

harmonic([0 1 -1 Inf -Inf])

ans =
     0     1   Inf   Inf   NaN

Harmonic Function for Symbolic Functions

Find the harmonic function for the symbolic function f.

syms f(x)
f(x) = exp(x) + tan(x);
y = harmonic(f)

y(x) =
harmonic(exp(x) + tan(x))

Harmonic Function for Symbolic Vectors and Matrices

Find the harmonic function for elements of vector V and matrix M.

syms x
V = [x sin(x) 3*i];
M = [exp(i*x) 2; -6 Inf];
harmonic(V)
harmonic(M)

ans =
[ harmonic(x), harmonic(sin(x)), harmonic(3i)]
ans =
[ harmonic(exp(x*1i)), 3/2]
[                Inf, Inf]

Plot Harmonic Function

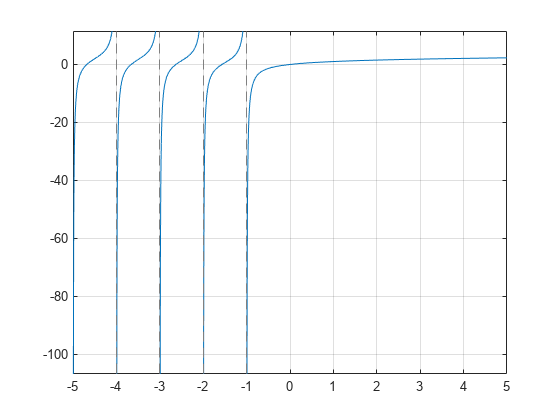
Plot the harmonic function from x = -5 to x = 5.

syms x
fplot(harmonic(x),[-5 5])
grid on

Differentiate and Find Limit of Harmonic Function

The functions diff and limit handle expressions containing harmonic.

Find the second derivative of harmonic(x^2+1).

syms x
diff(harmonic(x^2+1),x,2)

ans =
2*psi(1, x^2 + 2) + 4*x^2*psi(2, x^2 + 2)

Find the limit of harmonic(x) as x tends to ∞ and of (x+1)*harmonic(x) as x tends to -1.

syms x
limit(harmonic(x),Inf)
limit((x+1)*harmonic(x),-1)

ans =
Inf
ans =
-1

Taylor Series Expansion of Harmonic Function

Use taylor to expand the harmonic function in terms of the Taylor series.

syms x
taylor(harmonic(x))

ans =
(pi^6*x^5)/945 - zeta(5)*x^4 + (pi^4*x^3)/90...
 - zeta(3)*x^2 + (pi^2*x)/6

Expand Harmonic Function

Use expand to expand the harmonic function.

syms x
expand(harmonic(2*x+3))

ans =
harmonic(x + 1/2)/2 + log(2) + harmonic(x)/2 - 1/(2*(x + 1/2))...
 + 1/(2*x + 1) + 1/(2*x + 2) + 1/(2*x + 3)
 

Input Arguments

x — Input

number | vector | matrix | multidimensional array | symbolic variable | symbolic expression | symbolic function | symbolic vector | symbolic matrix | symbolic N-D array

Input, specified as number, vector, matrix, or as a multidimensional array or symbolic variable, expression, function, vector, matrix, or multidimensional array.

More About

Harmonic Function

The harmonic function for x is defined as

$$\mathrm{harmonic}\left(x\right)=\underset{k=1}{\overset{x}{\Sigma }}\frac{1}{k}$$

It is also defined as

$$\mathrm{harmonic}\left(x\right)=\Psi \left(x+1\right)+\gamma$$

where Ψ(x) is the polygamma function and γ is the Euler–Mascheroni constant.

Algorithms

The harmonic function is defined for all complex arguments z except for negative integers -1, -2,... where a singularity occurs.

If x has denominator 1, 2, 3, 4, or 6, then an explicit result is computed and returned. For other rational numbers, harmonic uses the functional equation $$\mathrm{harmonic}\left(x+1\right)=\mathrm{harmonic}\left(x\right)+\frac{1}{x}$$ to obtain a result with an argument x from the interval [0, 1].

expand expands harmonic using the equations $$\mathrm{harmonic}\left(x+1\right)=\mathrm{harmonic}\left(x\right)+\frac{1}{x}$$, $$\mathrm{harmonic}\left(-x\right)=\mathrm{harmonic}\left(x\right)-\frac{1}{x}+\pi \cot \left(\pi x\right)$$, and the Gauss multiplication formula for harmonic(kx), where k is an integer.

harmonic implements the following explicit formulae:

$$\mathrm{harmonic}\left(\frac{-1}{2}\right)=-2\ln \left(2\right)$$

$$\mathrm{harmonic}\left(-\frac{2}{3}\right)=-\frac{3}{2}\ln \left(3\right)-\frac{\sqrt{3}}{6}\pi$$

$$\mathrm{harmonic}\left(-\frac{1}{3}\right)=-\frac{3}{2}\ln \left(3\right)+\frac{\sqrt{3}}{6}\pi$$

$$\mathrm{harmonic}\left(\frac{-3}{4}\right)=-3\ln \left(2\right)-\frac{\pi }{2}$$

$$\mathrm{harmonic}\left(\frac{-1}{4}\right)=-3\ln \left(2\right)+\frac{\pi }{2}$$

$$\mathrm{harmonic}\left(\frac{-5}{6}\right)=-2\ln \left(2\right)-\frac{3}{2}\ln \left(3\right)-\frac{\sqrt{3}}{2}\pi$$

$$\mathrm{harmonic}\left(\frac{-1}{6}\right)=-2\ln \left(2\right)-\frac{3}{2}\ln \left(3\right)+\frac{\sqrt{3}}{2}\pi$$

$$\mathrm{harmonic}\left(0\right)=0$$

$$\mathrm{harmonic}\left(\frac{1}{2}\right)=2-2\ln \left(2\right)$$

$$\mathrm{harmonic}\left(\frac{1}{3}\right)=3-\frac{3}{2}\ln \left(3\right)-\frac{\sqrt{3}}{6}\pi$$

$$\mathrm{harmonic}\left(\frac{2}{3}\right)=\frac{3}{2}-\frac{3}{2}\ln \left(3\right)+\frac{\sqrt{3}}{6}\pi$$

$$\mathrm{harmonic}\left(\frac{1}{4}\right)=4-3\ln \left(2\right)-\frac{\pi }{2}$$

$$\mathrm{harmonic}\left(\frac{3}{4}\right)=\frac{4}{3}-3\ln \left(2\right)+\frac{\pi }{2}$$

$$\mathrm{harmonic}\left(\frac{1}{6}\right)=6-2\ln \left(2\right)-\frac{3}{2}\ln \left(3\right)-\frac{\sqrt{3}}{2}\pi$$

$$\mathrm{harmonic}\left(\frac{5}{6}\right)=\frac{6}{5}-2\ln \left(2\right)-\frac{3}{2}\ln \left(3\right)+\frac{\sqrt{3}}{2}\pi$$

$$\mathrm{harmonic}\left(1\right)=1$$

$$\mathrm{harmonic}\left(\infty \right)=\infty$$

$$\mathrm{harmonic}\left(-\infty \right)=NaN$$

Version History

Introduced in R2014a