euler

Euler numbers and polynomials

Syntax

euler(n)

euler(n,x)

Description

euler(n) returns the nth Euler number.

euler(n,x) returns the nth Euler polynomial.

Examples

Euler Numbers with Odd and Even Indices

The Euler numbers with even indices alternate the signs. Any Euler number with an odd index is 0.

Compute the even-indexed Euler numbers with the indices from 0 to 10:

euler(0:2:10)

ans =
           1          -1           5         -61...
        1385      -50521

Compute the odd-indexed Euler numbers with the indices from 1 to 11:

euler(1:2:11)

ans =
     0     0     0     0     0     0

Euler Polynomials

For the Euler polynomials, use euler with two input arguments.

Compute the first, second, and third Euler polynomials in variables x, y, and z, respectively:

syms x y z
euler(1, x)
euler(2, y)
euler(3, z)

ans =
x - 1/2
 
ans =
y^2 - y
 
ans =
z^3 - (3*z^2)/2 + 1/4

If the second argument is a number, euler evaluates the polynomial at that number. Here, the result is a floating-point number because the input arguments are not symbolic numbers:

euler(2, 1/3)

ans =
   -0.2222

To get the exact symbolic result, convert at least one number to a symbolic object:

euler(2, sym(1/3))

ans =
-2/9

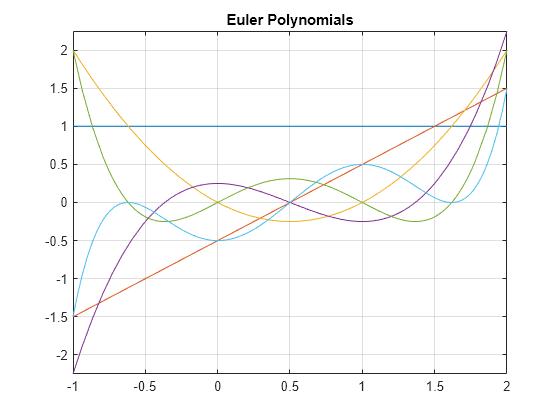
Plot Euler Polynomials

Plot the first six Euler polynomials.

syms x
fplot(euler(0:5, x), [-1 2])
title('Euler Polynomials')
grid on

Handle Expressions Containing Euler Polynomials

Many functions, such as diff and expand, can handle expressions containing euler.

Find the first and second derivatives of the Euler polynomial:

syms n x
diff(euler(n,x^2), x)

ans =
2*n*x*euler(n - 1, x^2)

diff(euler(n,x^2), x, x)

ans =
2*n*euler(n - 1, x^2) + 4*n*x^2*euler(n - 2, x^2)*(n - 1)

Expand these expressions containing the Euler polynomials:

expand(euler(n, 2 - x))

ans =
2*(1 - x)^n - (-1)^n*euler(n, x)

expand(euler(n, 2*x))

ans =
(2*2^n*bernoulli(n + 1, x + 1/2))/(n + 1) -...
(2*2^n*bernoulli(n + 1, x))/(n + 1)

Input Arguments

n — Index of the Euler number or polynomial

nonnegative integer | symbolic nonnegative integer | symbolic variable | symbolic expression | symbolic function | symbolic vector | symbolic matrix

Index of the Euler number or polynomial, specified as a nonnegative integer, symbolic nonnegative integer, variable, expression, function, vector, or matrix. If n is a vector or matrix, euler returns Euler numbers or polynomials for each element of n. If one input argument is a scalar and the other one is a vector or a matrix, euler(n,x) expands the scalar into a vector or matrix of the same size as the other argument with all elements equal to that scalar.

x — Polynomial variable

symbolic variable | symbolic expression | symbolic function | symbolic vector | symbolic matrix

Polynomial variable, specified as a symbolic variable, expression, function, vector, or matrix. If x is a vector or matrix, euler returns Euler numbers or polynomials for each element of x. When you use the euler function to find Euler polynomials, at least one argument must be a scalar or both arguments must be vectors or matrices of the same size. If one input argument is a scalar and the other one is a vector or a matrix, euler(n,x) expands the scalar into a vector or matrix of the same size as the other argument with all elements equal to that scalar.

More About

Euler Polynomials

The Euler polynomials are defined as follows:

$$\frac{2e^{xt}}{e^t+1}={\displaystyle \sum _{n=0}^{\infty }\mathrm{euler}\left(n,x\right)\frac{t^n}{n!}}$$

Euler Numbers

The Euler numbers are defined in terms of Euler polynomials as follows:

$$\mathrm{euler}\left(n\right)=2^n\mathrm{euler}\left(n,\frac{1}{2}\right)$$

Tips

• For the other meaning of Euler’s number, e = 2.71828…, call exp(1) to return the double-precision representation. For the exact representation of Euler’s number e, call exp(sym(1)).

• For the Euler–Mascheroni constant, see eulergamma.

Version History

Introduced in R2014a