dilog
Dilogarithm function
Syntax
Description
Examples
Dilogarithm Function for Numeric and Symbolic Arguments
Depending on its arguments, dilog returns
floating-point or exact symbolic results.
Compute the dilogarithm function for these numbers. Because these numbers are not
symbolic objects, dilog returns floating-point results.
A = dilog([-1, 0, 1/4, 1/2, 1, 2])
A = 2.4674 - 2.1776i 1.6449 + 0.0000i 0.9785 + 0.0000i... 0.5822 + 0.0000i 0.0000 + 0.0000i -0.8225 + 0.0000i
Compute the dilogarithm function for the numbers converted to symbolic objects. For
many symbolic (exact) numbers, dilog returns unresolved symbolic
calls.
symA = dilog(sym([-1, 0, 1/4, 1/2, 1, 2]))
symA = [ pi^2/4 - pi*log(2)*1i, pi^2/6, dilog(1/4), pi^2/12 - log(2)^2/2, 0, -pi^2/12]
Use vpa to approximate symbolic results with floating-point
numbers:
vpa(symA)
ans = [ 2.467401100272339654708622749969 - 2.1775860903036021305006888982376i,... 1.644934066848226436472415166646,... 0.97846939293030610374306666652456,... 0.58224052646501250590265632015968,... 0,... -0.82246703342411321823620758332301]
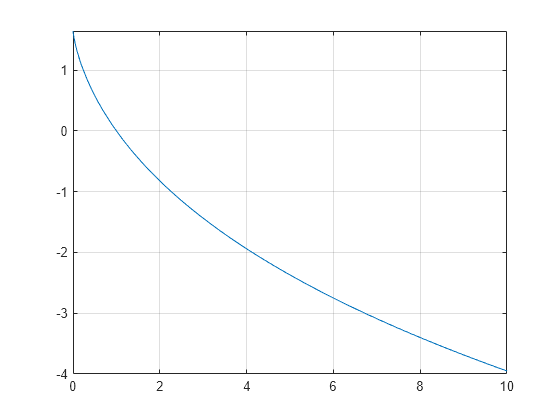
Plot Dilogarithm Function
Plot the dilogarithm function on the interval from 0 to 10.
syms x fplot(dilog(x),[0 10]) grid on
Handle Expressions Containing Dilogarithm Function
Many functions, such as diff,
int, and limit, can handle expressions
containing dilog.
Find the first and second derivatives of the dilogarithm function:
syms x diff(dilog(x), x) diff(dilog(x), x, x)
ans = -log(x)/(x - 1) ans = log(x)/(x - 1)^2 - 1/(x*(x - 1))
Find the indefinite integral of the dilogarithm function:
int(dilog(x), x)
ans = x*(dilog(x) + log(x) - 1) - dilog(x)
Find the limit of this expression involving dilog:
limit(dilog(x)/x, Inf)
ans = 0
Input Arguments
More About
Tips
dilog(sym(-1))returnspi^2/4 - pi*log(2)*i.dilog(sym(0))returnspi^2/6.dilog(sym(1/2))returnspi^2/12 - log(2)^2/2.dilog(sym(1))returns0.dilog(sym(2))returns-pi^2/12.dilog(sym(i))returnspi^2/16 - (pi*log(2)*i)/4 - catalan*i.dilog(sym(-i))returnscatalan*i + (pi*log(2)*i)/4 + pi^2/16.dilog(sym(1 + i))returns- catalan*i - pi^2/48.dilog(sym(1 - i))returnscatalan*i - pi^2/48.dilog(sym(Inf))returns-Inf.
References
[1] Stegun, I. A. “Miscellaneous Functions.” Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. (M. Abramowitz and I. A. Stegun, eds.). New York: Dover, 1972.
Version History
Introduced in R2014a