canonvars
Syntax
Description
Examples
Load the fisheriris data set.
load fisheririsThe column vector species contains iris flowers of three different species: setosa, versicolor, and virginica. The matrix meas contains four types of measurements for the flower: the length and width of sepals and petals in centimeters.
Perform a one-way MANOVA with species as the factor and the measurements in meas as the response variables.
maov = manova(species,meas);
maov is a one-way manova object that contains the results of the one-way MANOVA.
Calculate the canonical response data for maov.
canon = canonvars(maov)
canon = 150×4
-8.0618 0.3004 0.2784 0.0062
-7.1287 -0.7867 0.0008 0.8935
-7.4898 -0.2654 -0.5095 0.2211
-6.8132 -0.6706 -0.7477 -0.3347
-8.1323 0.5145 0.0120 -0.4802
-7.7019 1.4617 0.4307 -0.4431
-7.2126 0.3558 -0.9969 -0.4050
-7.6053 -0.0116 0.0625 -0.2491
-6.5606 -1.0152 -1.1122 0.0559
-7.3431 -0.9473 0.1042 -0.0990
-8.3974 0.6474 0.8728 -0.1636
-7.2193 -0.1096 -0.4196 -0.9909
-7.3268 -1.0730 -0.0669 0.2465
-7.5725 -0.8055 -1.1492 0.0443
-9.8498 1.5859 1.7501 0.8232
⋮
The output shows the canonical response data for the first ten observations. Each column of the output corresponds to a different canonical variable.
Create a scatter plot using the first and second canonical variables.
gscatter(canon(:,1),canon(:,2),species) xlabel("canon1") ylabel("canon2")
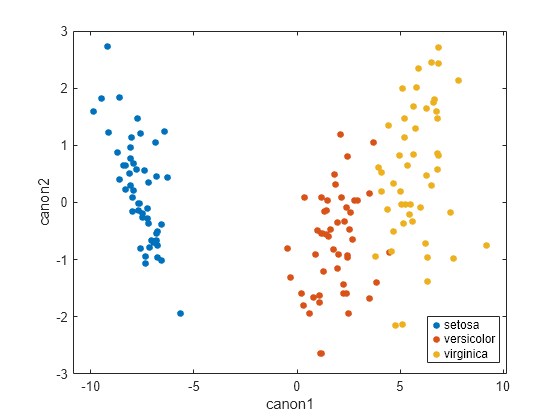
The function calculates the canonical variables by finding the lowest dimensional representation of the response variables that maximizes the correlation between the response variables and the factor values. The plot shows that the response data for the first two canonical variables is mostly separate for the different factor values. In particular, observations with the first canonical variable less than 0 correspond to the setosa group. Observations with the first canonical response variable greater than 0 and less than 5 correspond to the versicolor group. Finally, observations with the first canonical response variable greater than 5 correspond to the virginica group.
Load the carsmall data set.
load carsmallThe variable Model_Year contains data for the year a car was manufactured, and the variable Cylinders contains data for the number of engine cylinders in the car. The Acceleration and Displacement variables contain data for car acceleration and displacement.
Use the table function to create a table from the data in Model_Year and Cylinders.
tbl = table(Model_Year,Cylinders,VariableNames=["Year" "Cylinders"]);
Create a matrix of response variables from Acceleration and Displacement.
y = [Acceleration Displacement];
Perform a two-way MANOVA using the factor values in tbl and the response variables in y.
maov = manova(tbl,y);
maov is a two-way manova object that contains the results of the two-way MANOVA.
Return the canonical response data, canonical coefficients, and eigenvalues for the response data in maov, grouped by the Cylinders factor.
[canon,eigenvec,eigenval] = canonvars(maov,"Cylinders")canon = 100×2
2.9558 -0.5358
4.2381 -0.4096
3.2798 -0.8889
2.8661 -0.5600
2.7996 -1.2391
6.5913 -0.4348
7.3336 -0.6749
6.9131 -1.0089
7.3680 -0.2249
5.4195 -1.4126
-2.2174 0.4903
4.2381 -0.4096
4.2657 -0.6225
5.2194 -0.5852
4.5345 -0.5499
⋮
eigenvec = 2×2
0.0045 0.4419
0.0299 0.0081
eigenval = 2×1
6.5170
0.0808
The output shows the canonical response data for each canonical variable, and the vectors of canonical coefficients for each canonical variable with their corresponding eigenvalues.
You can use the coefficients in eigenvec to calculate canonical response data manually. Normalize the training data in maov.Y by using the mean function.
normres = maov.Y - mean(maov.Y)
normres = 100×2
-3.0280 99.4000
-3.5280 142.4000
-4.0280 110.4000
-3.0280 96.4000
-4.5280 94.4000
-5.0280 221.4000
-6.0280 246.4000
-6.5280 232.4000
-5.0280 247.4000
-6.5280 182.4000
2.4720 -74.6000
-3.5280 142.4000
-4.0280 143.4000
-4.5280 175.4000
-4.0280 152.4000
⋮
Calculate the product of the matrix of normalized response data and matrix of canonical coefficients.
mcanon = normres*eigenvec
mcanon = 100×2
2.9558 -0.5358
4.2381 -0.4096
3.2798 -0.8889
2.8661 -0.5600
2.7996 -1.2391
6.5913 -0.4348
7.3336 -0.6749
6.9131 -1.0089
7.3680 -0.2249
5.4195 -1.4126
-2.2174 0.4903
4.2381 -0.4096
4.2657 -0.6225
5.2194 -0.5852
4.5345 -0.5499
⋮
The first ten rows of mcanon are identical to the first ten rows of data in canon.
Check that mcanon is identical to canon by using the max and sum functions.
max(abs(canon-mcanon))
ans = 1×2
0 0
The zero output confirms that the two methods of calculating the canonical response data are equivalent.
Input Arguments
MANOVA results, specified as a manova object.
The properties of maov contain the factor values and response data
used by canonvars to calculate the canonical response
data.
Factor used to group the response data, specified as a string scalar or character array.
factor must be a name in
maov.FactorNames.
Example: "Factor2"
Data Types: char | string
Output Arguments
Canonical response data, returned as an n-by-r
numeric matrix. n is the number of observations in
maov, and r is the number of response
variables. To get the canonical response data, canonvars
normalizes the data in maov.Y and then calculates linear
combinations of the normalized data using the canonical coefficients. For more
information, see eigenvec.
Data Types: single | double
Canonical coefficients used to calculate the canonical response data, returned as an
r-by-r numeric matrix. r is
the number of response variables in maov.Y. Each column of
eigenvec corresponds to a different canonical variable. The
leftmost column of eigenvec corresponds to the canonical variable
that is the most correlated to the factor values, and the rightmost column corresponds
to the variable that is the least correlated. The canonical variables are uncorrelated
to each other. For more information, see Canonical Coefficients.
Data Types: single | double
Eigenvalues for the characteristic equation canonvars uses to
calculate the canonical coefficients, returned as an r-by-1 numeric
vector. For more information, see Canonical Coefficients.
Data Types: single | double
More About
The canonical coefficients are the r eigenvectors of the
characteristic equation
where H is the hypothesis matrix for
maov, E is the error matrix, and
r is the number of response variables.
The canonical variables correspond to projections of the response variables into linear
spaces with dimensions equal to or smaller than the number of response variables. The first
canonical variable is the projection of the response variables into the one-dimensional
Euclidean space that has the maximum correlation with the factor values. For 0 < n ≤ r, the nth canonical variable is the projection into the
one-dimensional Euclidean space that has the maximum correlation with the factor values,
subject to the constraint that the canonical variable is uncorrelated with the previous n – 1 canonical variables. For more information, see
Qe and
Qh in Multivariate Analysis of Variance for Repeated Measures.
Version History
Introduced in R2023b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)