Loguniform Distribution
Overview
The loguniform distribution (also called the reciprocal distribution) is a two-parameter distribution. This distribution has a probability density function that is proportional to the reciprocal of the variable value within its two bounding parameters (lower and upper limits of its support).
Create a probability distribution object LoguniformDistribution by specifying parameter values (makedist). Then, use object functions to evaluate the distribution,
generate random numbers, and so on.
Parameters
The loguniform distribution uses the following parameters.
| Parameter | Description | Support |
|---|---|---|
| a | Lower limit | 0 < a < b |
| b | Upper limit | a < b < ∞ |
Probability Density Function
The probability density function (pdf) of the loguniform distribution is
For an example, see Compute and Plot Loguniform Distribution pdf.
Cumulative Distribution Function
The cumulative distribution function (cdf) of the loguniform distribution is
The result p is the probability that a single observation from a loguniform distribution with parameters a and b falls in the interval [a x].
For an example, see Compute Loguniform Distribution cdf.
Descriptive Statistics
The mean of the loguniform distribution is .
The variance of the loguniform distribution is .
Examples
Compute and Plot Loguniform Distribution pdf
Create three loguniform distribution objects with different parameters.
pd1 = makedist('Loguniform') % Loguniform distribution with default parameters a = 1 and b = 4
pd1 =
LoguniformDistribution
Loguniform distribution
Lower = 1
Upper = 4
pd2 = makedist('Loguniform','lower',1,'upper',5); % Loguniform distribution with a = 1 and b = 5 pd3 = makedist('Loguniform','lower',2,'upper',6); % Loguniform distribution with a = 2 and b = 6
Compute the pdfs for the three loguniform distributions.
x = 0:.01:6; pdf1 = pdf(pd1,x); pdf2 = pdf(pd2,x); pdf3 = pdf(pd3,x);
Plot the pdfs on the same axis.
figure; plot(x,pdf1,'r','LineWidth',2); hold on; plot(x,pdf2,'k:','LineWidth',2); plot(x,pdf3,'b-.','LineWidth',2); legend({'a = 1, b = 4','a = 1, b = 5','a = 2, b = 6'},'Location','northwest'); xlabel('Observation') ylabel('Probability Density') hold off;
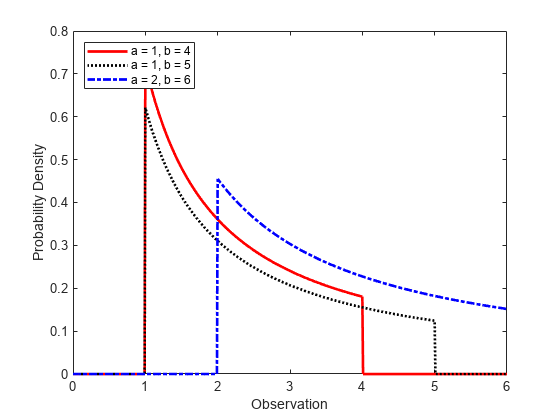
The distribution density is proportional to the reciprocal of the variable value within a and b, hence, the pdf value decreases as the value of the variable increases.
Compute Loguniform Distribution cdf
Create three loguniform distribution objects with different parameters.
pd1 = makedist('Loguniform'); % Loguniform distribution with default parameters a = 1 and b = 4 pd2 = makedist('Loguniform','lower',1,'upper',5); % Loguniform distribution with a = 1 and b = 5 pd3 = makedist('Loguniform','lower',2,'upper',6); % Loguniform distribution with a = 2 and b = 6
Compute the cdfs for the three loguniform distributions.
x = 1:.01:6; cdf1 = cdf(pd1,x); cdf2 = cdf(pd2,x); cdf3 = cdf(pd3,x);
Plot the cdfs on the same axis.
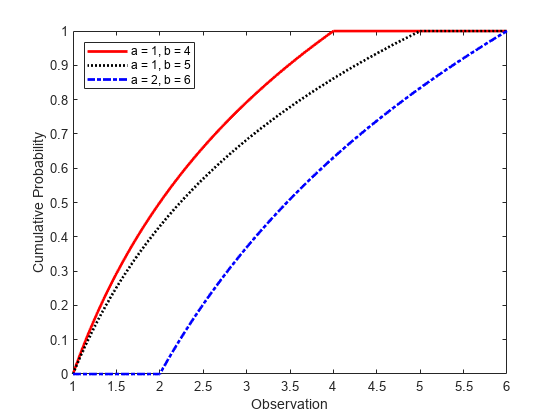
figure; plot(x,cdf1,'r','LineWidth',2); hold on; plot(x,cdf2,'k:','LineWidth',2); plot(x,cdf3,'b-.','LineWidth',2); legend({'a = 1, b = 4','a = 1, b = 5','a = 2, b = 6'},'Location','NW'); xlabel('Observation') ylabel('Cumulative Probability') hold off;
Transform Standard Uniform Sample to Loguniform Sample
Create a standard uniformly distributed sample of size 30.
p = random('Uniform',0,1,30,1);Compute the loguniform sample with support (2,7) corresponding to the standard uniform values in p.
logunifval = icdf('Loguniform',p,2,7);Alternatively, first create a loguniform distribution object with support (2,7) and then use it in the call to icdf.
logunifpd = makedist('Loguniform', "Lower",2,"Upper",7)
logunifpd =
LoguniformDistribution
Loguniform distribution
Lower = 2
Upper = 7
logunifval2 = icdf(logunifpd,p);
Generate Random Numbers from Loguniform Distribution
To generate random numbers from a loguniform distribution, you must first create a loguniform distribution object. Create a loguniform distribution object with support (3,10).
pd = makedist("Loguniform",3,10)pd =
LoguniformDistribution
Loguniform distribution
Lower = 3
Upper = 10
Generate a 3-by-4 matrix of random numbers from the loguniform distribution.
R = random(pd,3,4)
R = 3×4
8.0006 9.0096 4.1951 9.5861
8.9277 6.4235 5.7953 3.6269
3.4956 3.3738 9.5013 9.6521
Related Distributions
Uniform Distribution — The continuous uniform distribution is a two-parameter distribution that has parameters a (lower limit) and b (upper limit). If X has a loguniform distribution within the support a and b, then log(X) has a uniform distribution between log(a) and log(b).