linkage
Agglomerative hierarchical cluster tree
Syntax
Description
Examples
Input Arguments
Output Arguments
More About
Tips
Computing
linkage(y)can be slow whenyis a vector representation of the distance matrix. For the'centroid','median', and'ward'methods,linkagechecks whetheryis a Euclidean distance. Avoid this time-consuming check by passing inXinstead ofy.The
'centroid'and'median'methods can produce a cluster tree that is not monotonic. This result occurs when the distance from the union of two clusters, r and s, to a third cluster is less than the distance between r and s. In this case, in a dendrogram drawn with the default orientation, the path from a leaf to the root node takes some downward steps. To avoid this result, use another method. This figure shows a nonmonotonic cluster tree.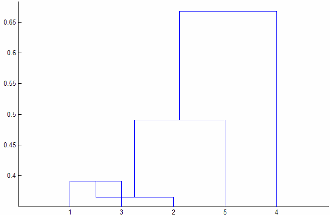
In this case, cluster 1 and cluster 3 are joined into a new cluster, and the distance between this new cluster and cluster 2 is less than the distance between cluster 1 and cluster 3. The result is a nonmonotonic tree.
You can provide the output
Zto other functions includingdendrogramto display the tree,clusterto assign points to clusters,inconsistentto compute inconsistent measures, andcophenetto compute the cophenetic correlation coefficient.
Version History
Introduced before R2006a
See Also
cluster | clusterdata | cophenet | dendrogram | inconsistent | kmeans | pdist | silhouette | squareform