Incremental Learning with Naive Bayes and Heterogeneous Data

This example shows how to prepare heterogeneous predictor data, containing real-valued and categorical measurements, for incremental learning using a naive Bayes classifier.

Naive Bayes classifiers for incremental learning support only numeric predictor data sets, but they can adapt to unseen categorical levels during training. If your data is heterogeneous and contained in a table, you must preprocess before performing incremental learning by following this general procedure:

1. Create a running hash map for each categorical variable by using container.Map MATLAB® objects. The hash map assigns a string to a unique numeric value, and it can easily adapt to new levels. Although you can create a cold hash map, this example assumes the first 50 observations from the data are available for populating a hash map and warming up the model.

2. Consistently concatenate all real-valued measurements with the numeric categorical levels.

Load and Preprocess Data

Load the 1994 US Census data set. The learning objective is to predict a US citizen's salary (salary, either <=50K or >50K) from several heterogeneous measurements on the citizen.

load census1994.mat

The training data is in the table adultdata. For details on the data set, enter Description.

Remove all observations containing at least one missing value from the data.

adultdata = adultdata(~any(ismissing(adultdata),2),:);
[n,p] = size(adultdata);
p = p - 1;  % Number of predictor variables    

Suppose only the first 50 observations are currently available.

n0 = 50;
sample0 = adultdata(1:n0,:);

Create Initial Hash Maps

Identify all categorical variables in the data, and determine their levels.

catpredidx = table2array(varfun(@iscategorical,adultdata(:,1:(end-1))));
numcatpreds = sum(catpredidx);
lvlstmp = varfun(@unique,adultdata(:,catpredidx),OutputFormat="cell");
lvls0 = cell(1,p);
lvls0(catpredidx) = lvlstmp;

For each categorical variable, create an initial hash map that assigns an integer, from 1 to the number of corresponding levels, to each level. Store all hash maps in a cell vector.

catmaps = cell(1,p);
J = find(catpredidx);

for j = J
    numlvls = numel(lvls0{j});
    catmaps{j} = containers.Map(cellstr(lvls0{j}),1:numlvls);
end
example1 = catmaps{find(catpredidx,1)}

example1 = 
  Map with properties:

        Count: 7
      KeyType: char
    ValueType: double

val = example1('Private')

val = 
3

catmaps is a numcatpreds-by-1 cell vector of containers.Map objects, each representing a hash map for the corresponding categorical variable. For example, the first hash map assigns 3 to the level 'Private'.

Represent Categorical Variables as Numeric

The supporting, local function processPredictorData has the following characteristics:

• Accept a table containing categorical and numeric variables, and the current cell vector of hash maps for each categorical variable.

• Return a matrix of homogenous, numeric predictor data with categorical variables replaced by numeric variables. The function replaces string-based levels with positive integers.

• Return an updated cell vector of hash maps when the input data contains variables with levels unknown to the current hash map.

Represent the categorical data in the initial sample as numeric by using processPredictorData.

[X0,catmaps] = processPredictorData(sample0(:,1:(end-1)),catmaps);
y0 = adultdata.salary(1:n0);

Fit Naive Bayes Model to Initial Sample

Fit a naive Bayes model to the initial sample. Identify the categorical variables.

Mdl = fitcnb(X0,y0,CategoricalPredictors=catpredidx);

Mdl is a ClassificationNaiveBayes model.

Prepare Naive Bayes Model for Incremental Learning

Convert the traditionally trained naive Bayes model to an incremental learner. Specify that the incremental model should base window metrics on 2000 observations.

IncrementalMdl = incrementalLearner(Mdl,MetricsWindowSize=2000);

IncrementalMdl is a warmed incrementalClassificationNaiveBayes object prepared for incremental learning. incrementalLearner initializes the parameters of the conditional distributions of the predictor variables with the values learned from the initial sample.

Perform Incremental Learning

Measure the model performance and fit the incremental model to the training data by using the updateMetricsAndFit function. Simulate a data stream by processing chunks of 100 observations at a time. At each iteration:

1. Process the predictor data and update the hash maps in the incoming 100 observations by using processPredictorData.

2. Fit a naive Bayes model to the processed data.

3. Overwrite the previous incremental model with a new one fitted to the incoming observations.

4. Store the current minimal cost and the learned conditional probability of selecting a female US citizen given each salary level.

numObsPerChunk = 100;
nchunks = floor(n/numObsPerChunk);
mc = array2table(zeros(nchunks,2),'VariableNames',["Cumulative" "Window"]);
catdistms = zeros(nchunks,2);
sexidx = string(adultdata.Properties.VariableNames) == "sex";
fidx = string(keys(catmaps{sexidx(1:end-1)})) == "Female";

for j = 1:nchunks
    ibegin = min(n,numObsPerChunk*(j-1) + 1 + n0);
    iend   = min(n,numObsPerChunk*j + n0);
    idx = ibegin:iend;
    [XChunk,catmaps] = processPredictorData(adultdata(idx,1:(end-1)),catmaps);
    IncrementalMdl = updateMetricsAndFit(IncrementalMdl,XChunk,adultdata.salary(idx));
    mc{j,:} = IncrementalMdl.Metrics{"MinimalCost",:};
    catdistms(j,1) = IncrementalMdl.DistributionParameters{1,sexidx}(fidx);
    catdistms(j,2) = IncrementalMdl.DistributionParameters{2,sexidx}(fidx);
end

IncrementalMdl is an incrementalClassificationNaiveBayes object incrementally fit to the entire stream. During incremental learning, updateMetricsAndFit checks the performance of the model on the incoming chunk of observations, and then fits the model to those observations.

Plot the cumulative and window minimal cost computed during incremental learning.

figure
plot(mc.Variables)
ylabel('Minimal Cost')
legend(mc.Properties.VariableNames)
xlabel('Iteration')

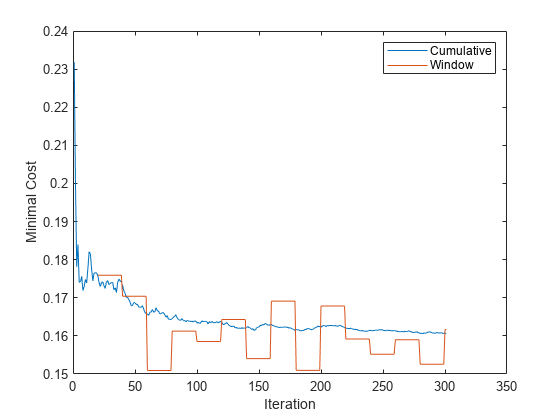
The cumulative loss gradually changes with each iteration (chunk of 100 observations), whereas the window loss jumps. Because the metrics window is 2000, updateMetricsAndFit measures the performance every 20 iterations.

Plot the running probability of selecting a female within each salary level.

figure
plot(catdistms)
ylabel('P(Female|Salary=y)')
legend(sprintf("y=%s",IncrementalMdl.ClassNames(1)),sprintf("y=%s",IncrementalMdl.ClassNames(2)))
xlabel('Iteration')

The fitted probabilities gradually settle during incremental learning.

Compare Performance on Test Data

Fit a naive Bayes classifier to the entire training data set.

MdlTT = fitcnb(adultdata,"salary");

MdlTT is a traditionally trained ClassificationNaiveBayes object.

Compute the minimal cost of the traditionally trained model on the test data adulttest.

adulttest = adulttest(~any(ismissing(adulttest),2),:); % Remove missing values
mctt = loss(MdlTT,adulttest)

mctt = 
0.1773

Process the predictors of the test data by using processPredictorData, and then compute the minimal cost of incremental learning model on the test data.

XTest = processPredictorData(adulttest(:,1:(end-1)),catmaps);
ilmc = loss(IncrementalMdl,XTest,adulttest.salary)

ilmc = 
0.1657

The minimal costs between the incremental model and the traditionally trained model are nearly the same.

Supporting Functions

function [Pred,maps] = processPredictorData(tbl,maps)
% PROCESSPREDICTORDATA Process heterogeneous data to homogeneous numeric
% data
%
% Input arguments:
%   tbl:  A table of raw input data
%   maps: A cell vector of container.Map hash maps.  Cells correspond to
%       categorical variables in tbl.
%
% Output arguments:
%   Pred: A numeric matrix of data with the same dimensions as tbl. Numeric
%   variables in tbl are assigned to the corresponding column of Pred,
%   categorical variables in tbl are processed and placed in the
%   corresponding column of Pred.

    catidx = varfun(@iscategorical,tbl,OutputFormat="uniform");
    numidx = ~catidx;
    numcats = sum(catidx);
    p = numcats + sum(numidx);
    currlvlstmp = varfun(@unique,tbl(:,catidx),OutputFormat="cell");
    currlvls0 = cell(1,p);
    currlvls0(catidx) = currlvlstmp;
    currlvlstmp = cellfun(@categories,currlvls0(catidx),UniformOutput=false);
    currlvls = cell(1,p);
    currlvls(catidx) = currlvlstmp;
    Pred = zeros(size(tbl));
    Pred(:,numidx) = tbl{:,numidx};
    J = find(catidx);
    for j = J
        hasNewlvl = ~isKey(maps{j},currlvls{j});
        if any(hasNewlvl)
            newcats = currlvls{j}(hasNewlvl);
            numnewcats = sum(hasNewlvl);
            g = numel(maps{j}.Count);
            for h = 1:numnewcats
                g = g + 1;
                maps{j}(newcats{h}) = g;
            end
        end
        conv2cell = cellstr(tbl{:,j});
        Pred(:,j) = cell2mat(values(maps{j},conv2cell));
    end
end