gmdistribution
Create Gaussian mixture model
Description
A gmdistribution object stores a Gaussian mixture
distribution, also called a Gaussian mixture model (GMM), which is a multivariate
distribution that consists of multivariate Gaussian distribution components. Each
component is defined by its mean and covariance. The mixture is defined by a vector of
mixing proportions, where each mixing proportion represents the fraction of the
population described by a corresponding component.
Creation
You can create a gmdistribution model object in two ways.
Use the
gmdistributionfunction (described here) to create agmdistributionmodel object by specifying the distribution parameters.Use the
fitgmdistfunction to fit agmdistributionmodel object to data given a fixed number of components.
Description
Input Arguments
Means of multivariate Gaussian distribution components,
specified as a k-by-m numeric matrix, where
k is the number of components and m is the number of
variables in each component. mu(i,:) is the mean of component
i.
Data Types: single | double
Covariances of multivariate Gaussian distribution components, specified as a numeric vector, matrix, or array.
Given that k is the number of components and
m is the number of variables in each component,
sigma is one of the values in this
table.
| Value | Description |
|---|---|
| m-by-m-by-k array | sigma(:,:,i) is the covariance
matrix of component i. |
| 1-by-m-by-k array | Covariance matrices are diagonal.
sigma(1,:,i) contains the
diagonal elements of the covariance matrix of
component i. |
| m-by-m matrix | Covariance matrices are the same across components. |
| 1-by-m vector | Covariance matrices are diagonal and the same across components. |
Data Types: single | double
Mixing proportions of mixture components, specified as a numeric
vector of length k, where k is the
number of components. The default is a row vector of
(1/k)s, which sets equal proportions. If
p does not sum to 1,
gmdistribution normalizes it.
Data Types: single | double
Properties
Distribution Parameters
This property is read-only.
Means of multivariate Gaussian distribution components,
specified as a k-by-m numeric matrix, where
k is the number of components and m is the number of
variables in each component. mu(i,:) is the mean of component
i.
Data Types: single | double
This property is read-only.
Covariances of multivariate Gaussian distribution components, specified as a numeric vector, matrix, or array.
Given that k is the number of components and
m is the number of variables in each component,
Sigma is one of the values in this
table.
| Value | Description |
|---|---|
| m-by-m-by-k array | Sigma(:,:,i) is the covariance
matrix of component i. |
| 1-by-m-by-k array | Covariance matrices are diagonal.
Sigma(1,:,i) contains the
diagonal elements of the covariance matrix of
component i. |
| m-by-m matrix | Covariance matrices are the same across components. |
| 1-by-m vector | Covariance matrices are diagonal and the same across components. |
Data Types: single | double
This property is read-only.
Mixing proportions of mixture components, specified as a 1-by-k numeric vector.
Data Types: single | double
Distribution Characteristics
This property is read-only.
Type of covariance matrices, specified as either
'diagonal' or 'full'.
If you create a
gmdistributionobject by using thegmdistributionfunction, then the type of covariance matrices in thesigmainput argument ofgmdistributionsets this property.If you fit a
gmdistributionobject to data by using thefitgmdistfunction, then the'CovarianceType'name-value pair argument offitgmdistsets this property.
This property is read-only.
Distribution name, specified as 'gaussian mixture
distribution'.
This property is read-only.
Number of mixture components, k, specified as a positive integer.
Data Types: single | double
This property is read-only.
Number of variables in the multivariate Gaussian distribution components, m, specified as a positive integer.
Data Types: double
This property is read-only.
Flag indicating whether a covariance matrix is shared across mixture
components, specified as true or
false.
If you create a
gmdistributionobject by using thegmdistributionfunction, then the type of covariance matrices in thesigmainput argument ofgmdistributionsets this property.If you fit a
gmdistributionobject to data by using thefitgmdistfunction, then the'SharedCovariance'name-value pair argument offitgmdistsets this property.
Data Types: logical
Properties for Fitted Object
The following properties apply only to a fitted object you create by using
fitgmdist. The values of these
properties are empty if you create a gmdistribution object by using
the gmdistribution function.
This property is read-only.
Akaike information criterion (AIC), specified as a scalar.
AIC = 2*NlogL + 2*p, where
NlogL is the negative loglikelihood (the
NegativeLogLikelihood property) and
p is the number of estimated parameters.
AIC is a model selection tool you can use to compare multiple models fit to the same data. AIC is a likelihood-based measure of model fit that includes a penalty for complexity, specifically, the number of parameters. When you compare multiple models, a model with a smaller value of AIC is better.
This property is empty if you create a gmdistribution object by using the gmdistribution function.
Data Types: single | double
This property is read-only.
Bayes information criterion (BIC), specified as a scalar. BIC
= 2*NlogL + p*log(n), where NlogL is
the negative loglikelihood (the
NegativeLogLikelihood property),
n is the number of observations, and
p is the number of estimated parameters.
BIC is a model selection tool you can use to compare multiple models fit to the same data. BIC is a likelihood-based measure of model fit that includes a penalty for complexity, specifically, the number of parameters. When you compare multiple models, a model with the lowest BIC value is the best fitting model.
This property is empty if you create a gmdistribution object by using the gmdistribution function.
Data Types: single | double
This property is read-only.
Flag indicating whether the Expectation-Maximization (EM) algorithm is
converged when fitting a Gaussian mixture model, specified as
true or false.
You can change the optimization options by using the 'Options'
name-value pair argument of fitgmdist.
This property is empty if you create a gmdistribution object by using the gmdistribution function.
Data Types: logical
This property is read-only.
Negative loglikelihood of the fitted Gaussian mixture model given the
input data X of
fitgmdist, specified as a scalar.
This property is empty if you create a gmdistribution object by using the gmdistribution function.
Data Types: single | double
This property is read-only.
Number of iterations in the Expectation-Maximization (EM) algorithm, specified as a positive integer.
You can change the optimization options, including the maximum number
of iterations allowed, by using the 'Options'
name-value pair argument of fitgmdist.
This property is empty if you create a gmdistribution object by using the gmdistribution function.
Data Types: double
This property is read-only.
Tolerance for posterior probabilities, specified as a nonnegative
scalar value in the range [0,1e-6].
The 'ProbabilityTolerance' name-value pair argument of
fitgmdist sets this property.
This property is empty if you create a gmdistribution object by using the gmdistribution function.
Data Types: single | double
This property is read-only.
Regularization parameter value, specified as a nonnegative scalar.
The 'RegularizationValue' name-value pair argument of
fitgmdist sets this property.
This property is empty if you create a gmdistribution object by using the gmdistribution function.
Data Types: single | double
Object Functions
cdf | Cumulative distribution function for Gaussian mixture distribution |
cluster | Construct clusters from Gaussian mixture distribution |
mahal | Mahalanobis distance to Gaussian mixture component |
pdf | Probability density function for Gaussian mixture distribution |
posterior | Posterior probability of Gaussian mixture component |
random | Random variate from Gaussian mixture distribution |
Examples
Create a two-component bivariate Gaussian mixture distribution by using the gmdistribution function.
Define the distribution parameters (means and covariances) of two bivariate Gaussian mixture components.
mu = [1 2;-3 -5];
sigma = cat(3,[2 .5],[1 1]) % 1-by-2-by-2 arraysigma =
sigma(:,:,1) =
2.0000 0.5000
sigma(:,:,2) =
1 1
The cat function concatenates the covariances along the third array dimension. The defined covariance matrices are diagonal matrices. sigma(1,:,i) contains the diagonal elements of the covariance matrix of component i.
Create a gmdistribution object. By default, the gmdistribution function creates an equal proportion mixture.
gm = gmdistribution(mu,sigma)
gm = Gaussian mixture distribution with 2 components in 2 dimensions Component 1: Mixing proportion: 0.500000 Mean: 1 2 Component 2: Mixing proportion: 0.500000 Mean: -3 -5
List the properties of the gm object.
properties(gm)
Properties for class gmdistribution:
NumVariables
DistributionName
NumComponents
ComponentProportion
SharedCovariance
NumIterations
RegularizationValue
NegativeLogLikelihood
CovarianceType
mu
Sigma
AIC
BIC
Converged
ProbabilityTolerance
You can access these properties by using dot notation. For example, access the ComponentProportion property, which represents the mixing proportions of mixture components.
gm.ComponentProportion
ans = 1×2
0.5000 0.5000
A gmdistribution object has properties that apply only to a fitted object. The fitted object properties are AIC, BIC, Converged, NegativeLogLikelihood, NumIterations, ProbabilityTolerance, and RegularizationValue. The values of the fitted object properties are empty if you create an object by using the gmdistribution function and specifying distribution parameters. For example, access the NegativeLogLikelihood property by using dot notation.
gm.NegativeLogLikelihood
ans =
[]
After you create a gmdistribution object, you can use the object functions. Use cdf and pdf to compute the values of the cumulative distribution function (cdf) and the probability density function (pdf). Use random to generate random vectors. Use cluster, mahal, and posterior for cluster analysis.
Visualize the object by using pdf and fsurf.
gmPDF = @(x,y) arrayfun(@(x0,y0) pdf(gm,[x0 y0]),x,y); fsurf(gmPDF,[-10 10])
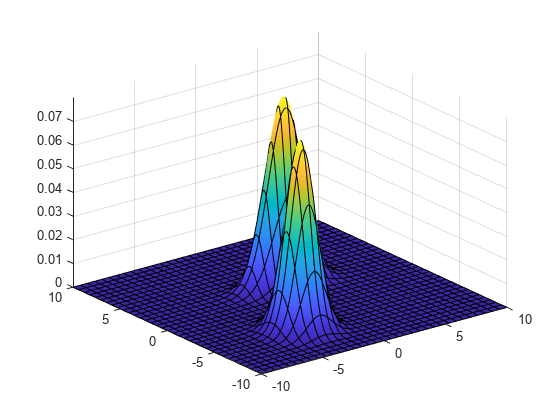
Generate random variates that follow a mixture of two bivariate Gaussian distributions by using the mvnrnd function. Fit a Gaussian mixture model (GMM) to the generated data by using the fitgmdist function.
Define the distribution parameters (means and covariances) of two bivariate Gaussian mixture components.
mu1 = [1 2]; % Mean of the 1st component sigma1 = [2 0; 0 .5]; % Covariance of the 1st component mu2 = [-3 -5]; % Mean of the 2nd component sigma2 = [1 0; 0 1]; % Covariance of the 2nd component
Generate an equal number of random variates from each component, and combine the two sets of random variates.
rng('default') % For reproducibility r1 = mvnrnd(mu1,sigma1,1000); r2 = mvnrnd(mu2,sigma2,1000); X = [r1; r2];
The combined data set X contains random variates following a mixture of two bivariate Gaussian distributions.
Fit a two-component GMM to X.
gm = fitgmdist(X,2)
gm = Gaussian mixture distribution with 2 components in 2 dimensions Component 1: Mixing proportion: 0.500000 Mean: -2.9617 -4.9727 Component 2: Mixing proportion: 0.500000 Mean: 0.9539 2.0261
List the properties of the gm object.
properties(gm)
Properties for class gmdistribution:
NumVariables
DistributionName
NumComponents
ComponentProportion
SharedCovariance
NumIterations
RegularizationValue
NegativeLogLikelihood
CovarianceType
mu
Sigma
AIC
BIC
Converged
ProbabilityTolerance
You can access these properties by using dot notation. For example, access the NegativeLogLikelihood property, which represents the negative loglikelihood of the data X given the fitted model.
gm.NegativeLogLikelihood
ans = 7.0584e+03
After you create a gmdistribution object, you can use the object functions. Use cdf and pdf to compute the values of the cumulative distribution function (cdf) and the probability density function (pdf). Use random to generate random variates. Use cluster, mahal, and posterior for cluster analysis.
Plot X by using scatter. Visualize the fitted model gm by using pdf and fcontour.
scatter(X(:,1),X(:,2),10,'.') % Scatter plot with points of size 10 hold on gmPDF = @(x,y) arrayfun(@(x0,y0) pdf(gm,[x0 y0]),x,y); fcontour(gmPDF,[-8 6])
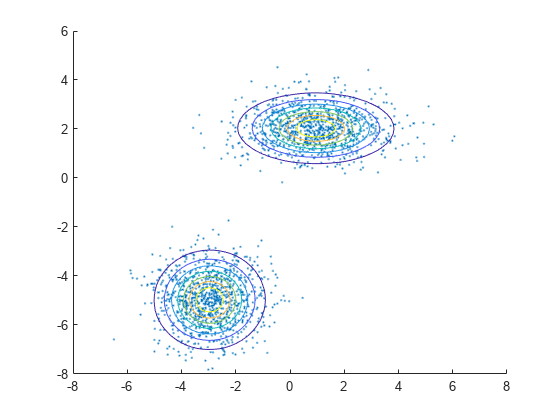
References
[1] McLachlan, G., and D. Peel. Finite Mixture Models. Hoboken, NJ: John Wiley & Sons, Inc., 2000.
Version History
Introduced in R2007b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)