Generalized Linear Model Workflow
This example shows how to fit a generalized linear model and analyze the results. A typical workflow involves these steps: import data, fit a generalized linear model, test its quality, modify the model to improve its quality, and make predictions based on the model. In this example, you use the Fisher iris data to compute the probability that a flower is in one of two classes.
Load Data
Load the Fisher iris data.
load fisheririsExtract rows 51 to 150, which have the classification versicolor or virginica.
X = meas(51:end,:);
Create logical response variables that are true for versicolor and false for virginica.
y = strcmp('versicolor',species(51:end));Fit Generalized Linear Model
Fit a binomial generalized linear model to the data.
mdl = fitglm(X,y,'linear','Distribution','binomial')
mdl =
Generalized linear regression model:
logit(y) ~ 1 + x1 + x2 + x3 + x4
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
________ ______ _______ ________
(Intercept) 42.638 25.708 1.6586 0.097204
x1 2.4652 2.3943 1.0296 0.30319
x2 6.6809 4.4796 1.4914 0.13585
x3 -9.4294 4.7372 -1.9905 0.046537
x4 -18.286 9.7426 -1.8769 0.060529
100 observations, 95 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 127, p-value = 1.95e-26
According to the model display, some p-values in the pValue column are not small, which implies that you can simplify the model.
Examine and Improve Model
Determine if 95% confidence intervals for the coefficients include 0. If so, you can remove the model terms with those intervals.
confint = coefCI(mdl)
confint = 5×2
-8.3984 93.6740
-2.2881 7.2185
-2.2122 15.5739
-18.8339 -0.0248
-37.6277 1.0554
Only the fourth predictor x3 has a coefficient whose confidence interval does not include 0.
The coefficients of x1 and x2 have large p-values and their 95% confidence intervals include 0. Test whether both coefficients can be zero. Specify a hypothesis matrix to select the coefficients of x1 and x2.
M = [0 1 0 0 0
0 0 1 0 0];
p = coefTest(mdl,M)p = 0.1442
The p-value is approximately 0.14, which is not small. Remove x1 and x2 from the model.
mdl1 = removeTerms(mdl,'x1 + x2')mdl1 =
Generalized linear regression model:
logit(y) ~ 1 + x3 + x4
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
________ ______ _______ __________
(Intercept) 45.272 13.612 3.326 0.00088103
x3 -5.7545 2.3059 -2.4956 0.012576
x4 -10.447 3.7557 -2.7816 0.0054092
100 observations, 97 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 118, p-value = 2.3e-26
Alternatively, you can identify important predictors using stepwiseglm.
mdl2 = stepwiseglm(X,y,'constant','Distribution','binomial','Upper','linear')
1. Adding x4, Deviance = 33.4208, Chi2Stat = 105.2086, PValue = 1.099298e-24 2. Adding x3, Deviance = 20.5635, Chi2Stat = 12.8573, PValue = 0.000336166 3. Adding x2, Deviance = 13.2658, Chi2Stat = 7.29767, PValue = 0.00690441
mdl2 =
Generalized linear regression model:
logit(y) ~ 1 + x2 + x3 + x4
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
________ ______ _______ ________
(Intercept) 50.527 23.995 2.1057 0.035227
x2 8.3761 4.7612 1.7592 0.078536
x3 -7.8745 3.8407 -2.0503 0.040334
x4 -21.43 10.707 -2.0014 0.04535
100 observations, 96 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 125, p-value = 5.4e-27
The p-value (pValue) for x2 in the coefficient table is greater than 0.05, but stepwiseglm includes x2 in the model because the p-value (PValue) for adding x2 is smaller than 0.05. The stepwiseglm function computes PValue using the fits with and without x2, whereas the function computes pValue based on an approximate standard error computed only from the final model. Therefore, PValue is more reliable than pValue.
Identify Outliers
Examine a leverage plot to look for influential outliers.
plotDiagnostics(mdl2,'leverage')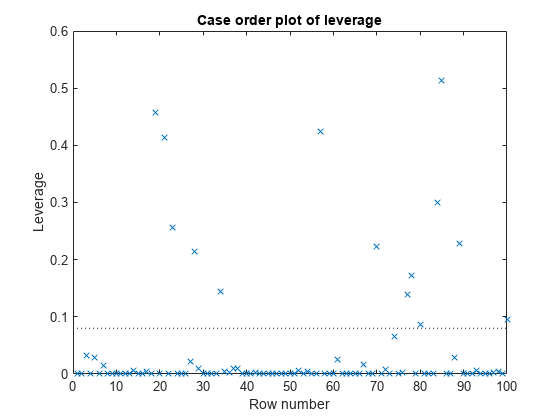
An observation can be considered an outlier if its leverage substantially exceeds p/n, where p is the number of coefficients and n is the number of observations. The dotted reference line is a recommended threshold, computed by 2*p/n, which corresponds to 0.08 in this plot. Some observations have leverage values larger than 10*p/n (that is, 0.40). Identify these observation points.
idxOutliers = find(mdl2.Diagnostics.Leverage > 10*mdl2.NumCoefficients/mdl2.NumObservations)
idxOutliers = 4×1
19
21
57
85
See if the model coefficients change when you fit a model excluding these points.
oldCoeffs = mdl2.Coefficients.Estimate; mdl3 = fitglm(X,y,'linear','Distribution','binomial', ... 'PredictorVars',2:4,'Exclude',idxOutliers); newCoeffs = mdl3.Coefficients.Estimate; disp([oldCoeffs newCoeffs])
50.5268 44.0085
8.3761 5.6361
-7.8745 -6.1145
-21.4296 -18.1236
The model coefficients in mdl3 are different from those in mdl2. This result implies that the responses at the high-leverage points are not consistent with the predicted values from the reduced model.
Predict Probability of Being Versicolor
Use mdl3 to predict the probability that a flower with average measurements is versicolor. Generate confidence intervals for the prediction.
[newf,newc] = predict(mdl3,mean(X))
newf = 0.4558
newc = 1×2
0.1234 0.8329
The model gives almost a 46% probability that the average flower is versicolor, with a wide confidence interval.
See Also
fitglm | stepwiseglm | GeneralizedLinearModel | predict | removeTerms | coefCI | plotDiagnostics