Ensemble Regularization
Regularization is a process of choosing fewer weak learners for an ensemble in a way that does not diminish predictive performance. Currently you can regularize regression ensembles. (You can also regularize a discriminant analysis classifier in a non-ensemble context; see Regularize Discriminant Analysis Classifier.)
The regularize method finds an optimal set of learner weights αt that minimize
Here
λ ≥ 0 is a parameter you provide, called the lasso parameter.
ht is a weak learner in the ensemble trained on N observations with predictors xn, responses yn, and weights wn.
g(f,y) = (f – y)2 is the squared error.
The ensemble is regularized on the same (xn,yn,wn) data used for training, so
is the ensemble resubstitution error. The error is measured by mean squared error (MSE).
If you use λ = 0, regularize finds the weak learner weights by minimizing the resubstitution MSE. Ensembles tend to overtrain. In other words, the resubstitution error is typically smaller than the true generalization error. By making the resubstitution error even smaller, you are likely to make the ensemble accuracy worse instead of improving it. On the other hand, positive values of λ push the magnitude of the αt coefficients to 0. This often improves the generalization error. Of course, if you choose λ too large, all the optimal coefficients are 0, and the ensemble does not have any accuracy. Usually you can find an optimal range for λ in which the accuracy of the regularized ensemble is better or comparable to that of the full ensemble without regularization.
A nice feature of lasso regularization is its ability to drive the optimized coefficients precisely to 0. If a learner's weight αt is 0, this learner can be excluded from the regularized ensemble. In the end, you get an ensemble with improved accuracy and fewer learners.
Regularize a Regression Ensemble
This example uses data for predicting the insurance risk of a car based on its many attributes.
Load the imports-85 data into the MATLAB® workspace.
load imports-85;Look at a description of the data to find the categorical variables and predictor names.
Description
Description = 9×79 char array
'1985 Auto Imports Database from the UCI repository '
'http://archive.ics.uci.edu/ml/machine-learning-databases/autos/imports-85.names'
'Variables have been reordered to place variables with numeric values (referred '
'to as "continuous" on the UCI site) to the left and categorical values to the '
'right. Specifically, variables 1:16 are: symboling, normalized-losses, '
'wheel-base, length, width, height, curb-weight, engine-size, bore, stroke, '
'compression-ratio, horsepower, peak-rpm, city-mpg, highway-mpg, and price. '
'Variables 17:26 are: make, fuel-type, aspiration, num-of-doors, body-style, '
'drive-wheels, engine-location, engine-type, num-of-cylinders, and fuel-system. '
The objective of this process is to predict the "symboling," the first variable in the data, from the other predictors. "symboling" is an integer from -3 (good insurance risk) to 3 (poor insurance risk). You could use a classification ensemble to predict this risk instead of a regression ensemble. When you have a choice between regression and classification, you should try regression first.
Prepare the data for ensemble fitting.
Y = X(:,1);
X(:,1) = [];
VarNames = {'normalized-losses' 'wheel-base' 'length' 'width' 'height' ...
'curb-weight' 'engine-size' 'bore' 'stroke' 'compression-ratio' ...
'horsepower' 'peak-rpm' 'city-mpg' 'highway-mpg' 'price' 'make' ...
'fuel-type' 'aspiration' 'num-of-doors' 'body-style' 'drive-wheels' ...
'engine-location' 'engine-type' 'num-of-cylinders' 'fuel-system'};
catidx = 16:25; % indices of categorical predictorsCreate a regression ensemble from the data using 300 trees.
ls = fitrensemble(X,Y,'Method','LSBoost','NumLearningCycles',300, ... 'LearnRate',0.1,'PredictorNames',VarNames, ... 'ResponseName','Symboling','CategoricalPredictors',catidx)
ls =
RegressionEnsemble
PredictorNames: {1×25 cell}
ResponseName: 'Symboling'
CategoricalPredictors: [16 17 18 19 20 21 22 23 24 25]
ResponseTransform: 'none'
NumObservations: 205
NumTrained: 300
Method: 'LSBoost'
LearnerNames: {'Tree'}
ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
FitInfo: [300×1 double]
FitInfoDescription: {2×1 cell}
Regularization: []
Properties, Methods
The final line, Regularization, is empty ([]). To regularize the ensemble, you have to use the regularize method.
cv = crossval(ls,'KFold',5); figure; plot(kfoldLoss(cv,'Mode','Cumulative')); xlabel('Number of trees'); ylabel('Cross-validated MSE'); ylim([0.2,2])

It appears you might obtain satisfactory performance from a smaller ensemble, perhaps one containing from 50 to 100 trees.
Call the regularize method to try to find trees that you can remove from the ensemble. By default, regularize examines 10 values of the lasso (Lambda) parameter spaced exponentially.
ls = regularize(ls)
ls =
RegressionEnsemble
PredictorNames: {1×25 cell}
ResponseName: 'Symboling'
CategoricalPredictors: [16 17 18 19 20 21 22 23 24 25]
ResponseTransform: 'none'
NumObservations: 205
NumTrained: 300
Method: 'LSBoost'
LearnerNames: {'Tree'}
ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
FitInfo: [300×1 double]
FitInfoDescription: {2×1 cell}
Regularization: [1×1 struct]
Properties, Methods
The Regularization property is no longer empty.
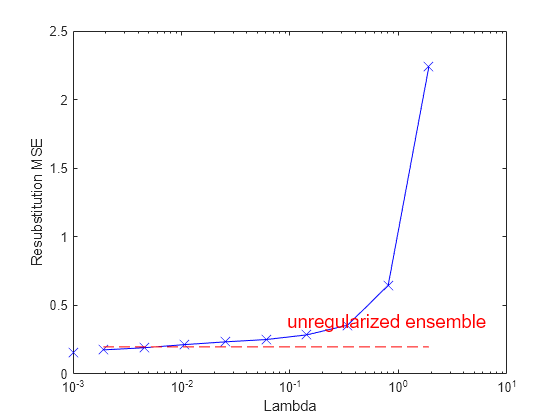
Plot the resubstitution mean-squared error (MSE) and number of learners with nonzero weights against the lasso parameter. Separately plot the value at Lambda = 0. Use a logarithmic scale because the values of Lambda are exponentially spaced.
figure; semilogx(ls.Regularization.Lambda,ls.Regularization.ResubstitutionMSE, ... 'bx-','Markersize',10); line([1e-3 1e-3],[ls.Regularization.ResubstitutionMSE(1) ... ls.Regularization.ResubstitutionMSE(1)],... 'Marker','x','Markersize',10,'Color','b'); r0 = resubLoss(ls); line([ls.Regularization.Lambda(2) ls.Regularization.Lambda(end)],... [r0 r0],'Color','r','LineStyle','--'); xlabel('Lambda'); ylabel('Resubstitution MSE'); annotation('textbox',[0.5 0.22 0.5 0.05],'String','unregularized ensemble', ... 'Color','r','FontSize',14,'LineStyle','none');
figure; loglog(ls.Regularization.Lambda,sum(ls.Regularization.TrainedWeights>0,1)); line([1e-3 1e-3],... [sum(ls.Regularization.TrainedWeights(:,1)>0) ... sum(ls.Regularization.TrainedWeights(:,1)>0)],... 'marker','x','markersize',10,'color','b'); line([ls.Regularization.Lambda(2) ls.Regularization.Lambda(end)],... [ls.NTrained ls.NTrained],... 'color','r','LineStyle','--'); xlabel('Lambda'); ylabel('Number of learners'); annotation('textbox',[0.3 0.8 0.5 0.05],'String','unregularized ensemble',... 'color','r','FontSize',14,'LineStyle','none');

The resubstitution MSE values are likely to be overly optimistic. To obtain more reliable estimates of the error associated with various values of Lambda, cross validate the ensemble using cvshrink. Plot the resulting cross-validation loss (MSE) and number of learners against Lambda.
rng(0,'Twister') % for reproducibility [mse,nlearn] = cvshrink(ls,'Lambda',ls.Regularization.Lambda,'KFold',5);
Warning: Some folds do not have any trained weak learners.
figure; semilogx(ls.Regularization.Lambda,ls.Regularization.ResubstitutionMSE, ... 'bx-','Markersize',10); hold on; semilogx(ls.Regularization.Lambda,mse,'ro-','Markersize',10); hold off; xlabel('Lambda'); ylabel('Mean squared error'); legend('resubstitution','cross-validation','Location','NW'); line([1e-3 1e-3],[ls.Regularization.ResubstitutionMSE(1) ... ls.Regularization.ResubstitutionMSE(1)],... 'Marker','x','Markersize',10,'Color','b','HandleVisibility','off'); line([1e-3 1e-3],[mse(1) mse(1)],'Marker','o',... 'Markersize',10,'Color','r','LineStyle','--','HandleVisibility','off');

figure; loglog(ls.Regularization.Lambda,sum(ls.Regularization.TrainedWeights>0,1)); hold;
Current plot held
loglog(ls.Regularization.Lambda,nlearn,'r--'); hold off; xlabel('Lambda'); ylabel('Number of learners'); legend('resubstitution','cross-validation','Location','NE'); line([1e-3 1e-3],... [sum(ls.Regularization.TrainedWeights(:,1)>0) ... sum(ls.Regularization.TrainedWeights(:,1)>0)],... 'Marker','x','Markersize',10,'Color','b','HandleVisibility','off'); line([1e-3 1e-3],[nlearn(1) nlearn(1)],'marker','o',... 'Markersize',10,'Color','r','LineStyle','--','HandleVisibility','off');

Examining the cross-validated error shows that the cross-validation MSE is almost flat for Lambda up to a bit over 1e-2.
Examine ls.Regularization.Lambda to find the highest value that gives MSE in the flat region (up to a bit over 1e-2).
jj = 1:length(ls.Regularization.Lambda); [jj;ls.Regularization.Lambda]
ans = 2×10
1.0000 2.0000 3.0000 4.0000 5.0000 6.0000 7.0000 8.0000 9.0000 10.0000
0 0.0019 0.0045 0.0107 0.0254 0.0602 0.1428 0.3387 0.8033 1.9048
Element 5 of ls.Regularization.Lambda has value 0.0254, the largest in the flat range.
Reduce the ensemble size using the shrink method. shrink returns a compact ensemble with no training data. The generalization error for the new compact ensemble was already estimated by cross validation in mse(5).
cmp = shrink(ls,'weightcolumn',5)cmp =
CompactRegressionEnsemble
PredictorNames: {1×25 cell}
ResponseName: 'Symboling'
CategoricalPredictors: [16 17 18 19 20 21 22 23 24 25]
ResponseTransform: 'none'
NumTrained: 8
Properties, Methods
The number of trees in the new ensemble has notably reduced from the 300 in ls.
Compare the sizes of the ensembles.
sz(1) = whos('cmp'); sz(2) = whos('ls'); [sz(1).bytes sz(2).bytes]
ans = 1×2
96476 3390153
The size of the reduced ensemble is a fraction of the size of the original. Note that your ensemble sizes can vary depending on your operating system.
Compare the MSE of the reduced ensemble to that of the original ensemble.
figure; plot(kfoldLoss(cv,'mode','cumulative')); hold on plot(cmp.NTrained,mse(5),'ro','MarkerSize',10); xlabel('Number of trees'); ylabel('Cross-validated MSE'); legend('unregularized ensemble','regularized ensemble',... 'Location','NE'); hold off

The reduced ensemble gives low loss while using many fewer trees.
See Also
fitrensemble | regularize | kfoldLoss | cvshrink | shrink | resubLoss | crossval