predictorImportance
Estimates of predictor importance for classification tree
Description
imp = predictorImportance(tree)tree by summing changes in
the risk due to splits on every predictor and dividing the sum by the number of branch
nodes. imp is returned as a row vector with the same number of elements
as tree.PredictorNames. The entries of imp are
estimates of the predictor importance, with 0 representing the smallest
possible importance.
Examples
Estimate Predictor Importance Values
Load Fisher's iris data set.
load fisheririsGrow a classification tree.
Mdl = fitctree(meas,species);
Compute predictor importance estimates for all predictor variables.
imp = predictorImportance(Mdl)
imp = 1×4
0 0 0.0907 0.0682
The first two elements of imp are zero. Therefore, the first two predictors do not enter into Mdl calculations for classifying irises.
Estimates of predictor importance do not depend on the order of predictors if you use surrogate splits, but do depend on the order if you do not use surrogate splits.
Permute the order of the data columns in the previous example, grow another classification tree, and then compute predictor importance estimates.
measPerm = meas(:,[4 1 3 2]); MdlPerm = fitctree(measPerm,species); impPerm = predictorImportance(MdlPerm)
impPerm = 1×4
0.1515 0 0.0074 0
The estimates of predictor importance are not a permutation of imp.
Surrogate Splits and Predictor Importance
Load Fisher's iris data set.
load fisheririsGrow a classification tree. Specify usage of surrogate splits.
Mdl = fitctree(meas,species,'Surrogate','on');
Compute predictor importance estimates for all predictor variables.
imp = predictorImportance(Mdl)
imp = 1×4
0.0791 0.0374 0.1530 0.1529
All predictors have some importance. The first two predictors are less important than the final two.
Permute the order of the data columns in the previous example, grow another classification tree specifying usage of surrogate splits, and then compute predictor importance estimates.
measPerm = meas(:,[4 1 3 2]); MdlPerm = fitctree(measPerm,species,'Surrogate','on'); impPerm = predictorImportance(MdlPerm)
impPerm = 1×4
0.1529 0.0791 0.1530 0.0374
The estimates of predictor importance are a permutation of imp.
Unbiased Predictor Importance Estimates
Load the census1994 data set. Consider a model that predicts a person's salary category given their age, working class, education level, martial status, race, sex, capital gain and loss, and number of working hours per week.
load census1994 X = adultdata(:,{'age','workClass','education_num','marital_status','race',... 'sex','capital_gain','capital_loss','hours_per_week','salary'});
Display the number of categories represented in the categorical variables using summary.
summary(X)
Variables:
age: 32561x1 double
Values:
Min 17
Median 37
Max 90
workClass: 32561x1 categorical
Values:
Federal-gov 960
Local-gov 2093
Never-worked 7
Private 22696
Self-emp-inc 1116
Self-emp-not-inc 2541
State-gov 1298
Without-pay 14
NumMissing 1836
education_num: 32561x1 double
Values:
Min 1
Median 10
Max 16
marital_status: 32561x1 categorical
Values:
Divorced 4443
Married-AF-spouse 23
Married-civ-spouse 14976
Married-spouse-absent 418
Never-married 10683
Separated 1025
Widowed 993
race: 32561x1 categorical
Values:
Amer-Indian-Eskimo 311
Asian-Pac-Islander 1039
Black 3124
Other 271
White 27816
sex: 32561x1 categorical
Values:
Female 10771
Male 21790
capital_gain: 32561x1 double
Values:
Min 0
Median 0
Max 99999
capital_loss: 32561x1 double
Values:
Min 0
Median 0
Max 4356
hours_per_week: 32561x1 double
Values:
Min 1
Median 40
Max 99
salary: 32561x1 categorical
Values:
<=50K 24720
>50K 7841
Because there are few categories represented in the categorical variables compared to levels in the continuous variables, the standard CART, predictor-splitting algorithm prefers splitting a continuous predictor over the categorical variables.
Train a classification tree using the entire data set. To grow unbiased trees, specify usage of the curvature test for splitting predictors. Because there are missing observations in the data, specify usage of surrogate splits.
Mdl = fitctree(X,'salary','PredictorSelection','curvature',... 'Surrogate','on');
Estimate predictor importance values by summing changes in the risk due to splits on every predictor and dividing the sum by the number of branch nodes. Compare the estimates using a bar graph.
imp = predictorImportance(Mdl); figure; bar(imp); title('Predictor Importance Estimates'); ylabel('Estimates'); xlabel('Predictors'); h = gca; h.XTickLabel = Mdl.PredictorNames; h.XTickLabelRotation = 45; h.TickLabelInterpreter = 'none';
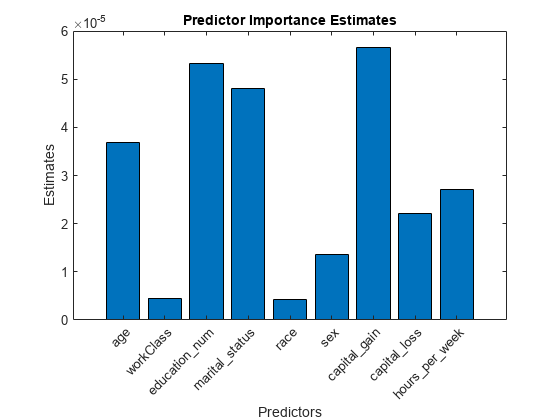
In this case, capital_gain is the most important predictor, followed by education_num.
Input Arguments
tree — Trained classification tree
ClassificationTree model object | CompactClassificationTree model object
Trained classification tree, specified as a ClassificationTree model object trained with fitctree, or a CompactClassificationTree model object
created with compact.
More About
Predictor Importance
predictorImportance computes importance measures of the predictors in a tree by
summing changes in the node risk due to splits on every predictor, and then dividing the sum
by the total number of branch nodes. The change in the node risk is the difference between
the risk for the parent node and the total risk for the two children. For example, if a tree
splits a parent node (for example, node 1) into two child nodes (for example, nodes 2 and
3), then predictorImportance increases the importance of the split predictor by
(R1 – R2 – R3)/Nbranch,
where Ri is the node risk of node i, and Nbranch is the total number of branch nodes. A node risk is defined as a node error or node impurity weighted by the node probability:
Ri = PiEi,
where Pi is the node probability of node i, and Ei is either the node error (for a tree grown by minimizing the twoing criterion) or node impurity (for a tree grown by minimizing an impurity criterion, such as the Gini index or deviance) of node i.
The estimates of predictor importance depend on whether you use surrogate splits for training.
If you use surrogate splits,
predictorImportancesums the changes in the node risk over all splits at each branch node, including surrogate splits. If you do not use surrogate splits, then the function takes the sum over the best splits found at each branch node.Estimates of predictor importance do not depend on the order of predictors if you use surrogate splits, but do depend on the order if you do not use surrogate splits.
If you use surrogate splits,
predictorImportancecomputes estimates before the tree is reduced by pruning (or merging leaves). If you do not use surrogate splits,predictorImportancecomputes estimates after the tree is reduced by pruning. Therefore, pruning affects the predictor importance for a tree grown without surrogate splits, and does not affect the predictor importance for a tree grown with surrogate splits.
Impurity and Node Error
A decision tree splits nodes based on either impurity or node error.
Impurity means one of several things, depending on your choice of the
SplitCriterion name-value
argument:
Gini's Diversity Index (
gdi) — The Gini index of a node iswhere the sum is over the classes i at the node, and p(i) is the observed fraction of classes with class i that reach the node. A node with just one class (a pure node) has Gini index
0; otherwise, the Gini index is positive. So the Gini index is a measure of node impurity.Deviance (
"deviance") — With p(i) defined the same as for the Gini index, the deviance of a node isA pure node has deviance
0; otherwise, the deviance is positive.Twoing rule (
"twoing") — Twoing is not a purity measure of a node, but is a different measure for deciding how to split a node. Let L(i) denote the fraction of members of class i in the left child node after a split, and R(i) denote the fraction of members of class i in the right child node after a split. Choose the split criterion to maximizewhere P(L) and P(R) are the fractions of observations that split to the left and right, respectively. If the expression is large, the split made each child node purer. Similarly, if the expression is small, the split made each child node similar to each other and, therefore, similar to the parent node. The split did not increase node purity.
Node error — The node error is the fraction of misclassified classes at a node. If j is the class with the largest number of training samples at a node, the node error is
1 – p(j).
Extended Capabilities
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2011a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)