Resolver
Rotary transformer that measures angle of rotation
Libraries:
Simscape /
Electrical /
Sensors & Transducers
Description
The Resolver block models a generic resolver, which measures the electrical phase angle of a signal through electromagnetic coupling. The resolver consists of a rotary transformer that couples an AC voltage applied to the primary winding to two secondary windings. These secondary windings are physically oriented at 90 degrees to each other. As the rotor angle changes, the relative coupling between the primary and the two secondary windings varies. In the Resolver block model, the first secondary winding is oriented such that peak coupling occurs when the rotor is at zero degrees, and therefore the second secondary winding has minimum coupling when the rotor is at zero degrees.
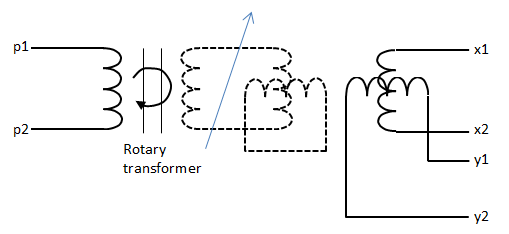
Without loss of generality, it is assumed that the transformer between primary and rotor circuit is ideal with a ratio of 1:1. This results in the rotor current and voltage being equivalent to the primary current and voltage.
You have two options for defining the block equations:
Omit the dynamics by neglecting the transformer inductive terms. This model is only valid if the sensor is driven by a sine wave because any DC component on the primary side will pass to the output side.
Include the inductive terms, thereby capturing voltage amplitude loss and phase differences. This model is valid for any input waveform. Within this option, you can either specify the inductances and the peak coupling coefficient directly, or specify the transformation ratio and measured impedances, in which case the block uses these values to determine the inductive terms.
Equations when Omitting Dynamics
The equations are based on the superposition of two ideal transformers, both with coupling coefficients that depend on rotor angle. The two ideal transformers have a common primary winding. See the Simscape™ Ideal Transformer block reference page for more information on modeling ideal transformers. The equations are:
Kx = R cos( N Θ )
Ky = R sin( N Θ )
vx = Kx v p
vy = Ky v p
ip = – Kx ix – Ky iy
where:
vp and ip are the rotor (or equivalently primary) voltage and current, respectively.
vx and ix are the first secondary voltage and current, respectively.
vy and iy are the second secondary voltage and current, respectively.
Kx is the coupling coefficient for the first secondary winding.
Ky is the coupling coefficient for the second secondary winding.
R is the transformation ratio.
N is the number of pole pairs.
Θ is the rotor angle.
Equations when Including Dynamics
The equations are based on the superposition of two mutual inductors, both with coupling coefficients that depend on rotor angle. The two mutual inductors have a common primary winding. See the Simscape Mutual Inductor block reference page for more information on modeling mutual inductors. The equations are:
where:
vp and ip are the rotor (or equivalently primary) voltage and current, respectively.
vx and ix are the first secondary voltage and current, respectively.
vy and iy are the second secondary voltage and current, respectively.
Rp is the rotor (or primary) resistance.
Lp is the rotor (or primary) inductance.
Rs is the stator (or secondary) resistance.
Ls is the stator (or secondary) inductance.
N is the number of pole pairs.
k is the coefficient of coupling.
Θ is the rotor angle.
It is assumed that coupling between the two secondary windings is zero.
Datasheets typically do not quote the coefficient of coupling and inductance
parameters, but instead give the transformation ratio R and measured impedances. If
you select Specify transformation ratio and measured
impedances for the Parameterization
parameter, then the values you provide are used to determine values for the equation
coefficients, as defined above.
Variables
To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Use nominal values to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources. One of these sources is the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.
Examples
Assumptions and Limitations
The resolver draws no torque between the mechanical rotational ports R and C.
The transformer between primary and rotor circuit is ideal with a ratio of 1:1.
The coupling between the two secondary windings is zero.
Ports
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2017b