Induction Machine (Single-Phase)
Single-phase induction machine with SI or pu fundamental parameterization
Libraries:
Simscape /
Electrical /
Electromechanical /
Asynchronous
Description
The Induction Machine (Single-Phase) block represents a single-phase induction machine with a squirrel cage rotor with fundamental parameters expressed in per-unit or in the International System of Units (SI).
This block models four types of single-phase induction machines:
Split-phaseCapacitor-startCapacitor-start-capacitor-runMain and auxiliary windings
The single phase induction machine consists of a squirrel cage rotor and two stator windings, the main and the auxiliary windings. The auxiliary winding is typically only active during startup. However, to improve performance, the auxiliary winding can be active during running for low-power applications. The figure shows the equivalent d- and q-axis circuits for the main and auxiliary windings.

The table defines the variables.
| Variable | Definition |
|---|---|
| vqsvds | Stator voltages in the d-q representation |
| iqsids | Stator currents in the d-q representation |
| ΨqrΨdr | Rotor fluxes in the d-q representation |
| ⍵ | Rotor electrical speed |
| a | Auxiliary/main windings turn ratio |
| Ras | Main winding stator resistance |
| Las | Main winding stator leakage inductance |
| R'ar | Main winding rotor resistance |
| L'lar | Main winding rotor leakage inductance |
| Lmas | Main winding mutual inductance |
| Rbs | Auxiliary winding stator resistance |
| Rlbs | Auxiliary winding stator leakage inductance |
| R'br | Auxiliary winding rotor resistance |
| L'lbr | Auxiliary winding rotor leakage inductance |
| Lmbs | Auxiliary winding mutual inductance |
Equations
The SI model converts the SI values that you enter in the dialog box to per-unit values for simulation. For information on the relationship between SI and per-unit machine parameters, see Per-Unit Conversion for Machine Parameters. For information on per-unit parameterization, see Per-Unit System of Units.
These transformations reduce the rotor resistance, rotor leakage inductance, and stator mutual inductance to a single set of values by defining the equivalent circuits with respect to the main winding:
The voltage equations for the stator and rotor are:
The expression for the electromagnetic torque, T, is obtained by applying the principle of virtual displacement [1].
The mechanical equation is
where ωm is the rotor angular velocity.
In split-phase machines, the auxiliary winding is displaced at 90 electrical degrees from the main winding and operates only until the speed reaches the disconnection speed, which is typically 70 to 80 percent of rated speed. In this configuration, the auxiliary winding has high resistance and small reactance compared to the main winding. The resulting phase difference makes the machine behave like a two-phase machine.
The capacitor-start machine is a type of split-phase machine that uses a capacitor in series with the auxiliary winding to start the machine. In this configuration, auxiliary and main windings have the same number of turns. The value of the capacitor ensures that the current in the auxiliary coil leads the current in the main winding by approximately 80 electrical degrees.
The capacitor-start voltage is:
When a capacitor is connected in series with the auxiliary winding, the voltage equation for the d-axis is
The extension is obtained immediately for capacitor-start-capacitor-run machines. In this configuration, two capacitors are connected in parallel.

The d-axis voltage after disconnecting the capacitor-start is
Display Option
To display the machine per-unit base values in the MATLAB® Command Window, right-click the block and, from the Electrical menu, select Display Base Values.
Model Thermal Effects
You can expose thermal ports to simulate the effects of generated heat and motor temperature. To expose the thermal ports and the Thermal parameters, set the Modeling option parameter to either:
No thermal port— The block contains electrical conserving ports associated with the stator windings, but does not contain thermal ports.Show thermal port— The block contains expanded electrical conserving ports associated with the stator windings and thermal conserving ports for each of the windings and for the rotor.
For more information about using thermal ports in actuator blocks, see Simulating Thermal Effects in Rotational and Translational Actuators.
Variables
To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. You can specify nominal values using different sources, including the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.
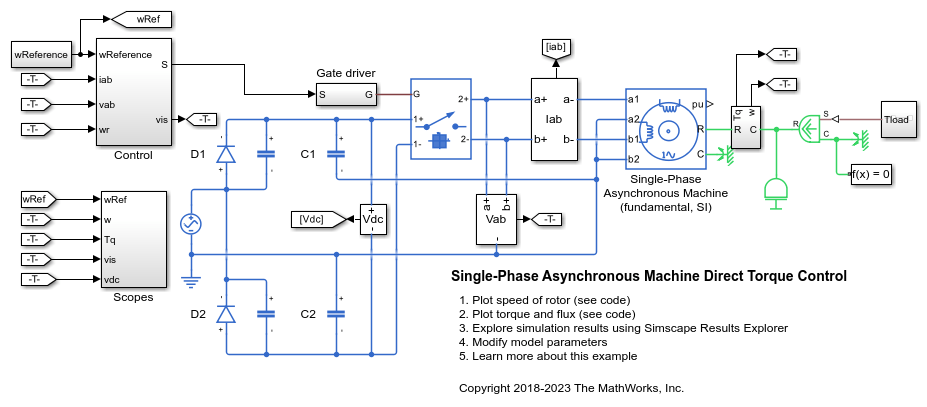
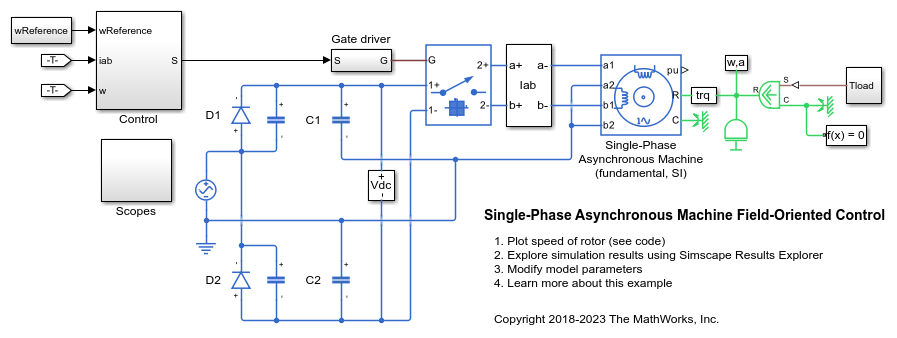
Examples
Ports
Output
Conserving
Parameters
References
[1] Krause, P. C. "Simulation of Unsymmetrical 2-Phase Induction Machines." IEEE Transactions on Power Apparatus and Systems. Vol 84, Number 11, 1965, pp. 1025-1037.