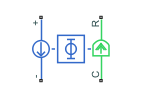
FEM-Parameterized Linear Actuator
Linear actuator defined in terms of magnetic flux
Libraries:
Simscape /
Electrical /
Electromechanical /
Mechatronic Actuators
Description
The FEM-Parameterized Linear Actuator block implements a model of a linear actuator defined in terms of magnetic flux. Use this block to model custom solenoids and linear motors where magnetic flux depends on both distance and current. You parameterize the block using data from a third-party magnetic finite-element method (FEM) package.
Note
To use this block to represent a solenoid with air gap x between case C and plunger R, then the tabulated force should be negative to represent the pulling force bringing R towards C.
The block has two options for the electrical equation. The first,
Define in terms of dPhi(i,x)/dx and
dPhi(i,x)/di, defines the current in terms of partial
derivatives of the magnetic flux (Φ) with respect to distance
(x) and current (i), the
equations for which are:
The second option, Define in terms of Phi(i,x),
defines the voltage across the component directly in terms of the flux, the
equation for which is:
Numerically, defining the electrical equation in terms of flux partial derivatives is better because the back-emf is piecewise continuous. If using the flux directly, using a finer grid size for current and position will improve results, as will selecting cubic or spline interpolation.
In both cases, you have an option to either directly specify the force as a function of current and position, by using the Force matrix, F(i,x) parameter, or have the block automatically calculate the force matrix.
If entering the electromagnetic force data directly, you can either use data supplied by the finite element magnetic package (which you used to determine the flux) or calculate the force from the flux with following equation:
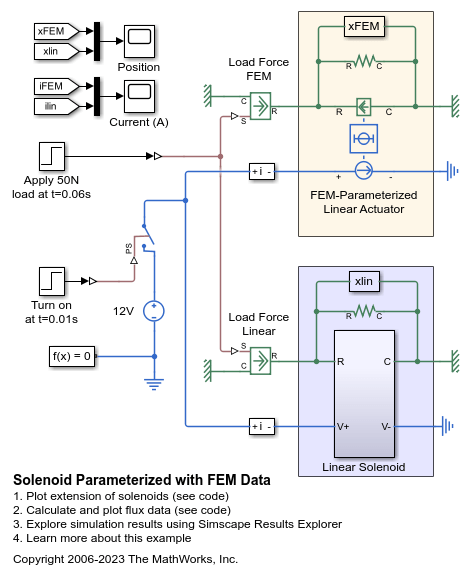
For an example that shows how to implement this type of integration in
MATLAB®, see Solenoid Parameterized with FEM Data. The related file
ee_solenoid_fem_params.m contains
the code that calculates and plots the flux data.
Alternatively, the block can automatically calculate the force matrix from the
flux information that you provide. To select this option, set the
Calculate force matrix? parameter to
Yes. The force matrix calculation occurs
at model initialization based on current block flux linkage information. The
force is calculated by numerically integrating the rate of change of flux
linkage with respect to position over current, according to the preceding
equation. If the Electrical model parameter is set to
Define in terms of Phi(i,x), then the
block must first estimate the Flux partial derivative wrt
displacement, dPhi(i,x)/dx parameter value from the flux
linkage data. When doing this, the block uses the interpolation method
specified by the Interpolation method parameter.
Typically, the Smooth option is most accurate,
but the Linear option is most robust.
You can define Φ and its partial derivatives for just positive, or positive and negative currents. If defining for just positive currents, then the block assumes that Φ(–i,x) = –Φ(i,x). Therefore, if the current vector is positive only:
The first current value must be zero.
The flux corresponding to zero current must be zero.
The partial derivative of flux with respect to displacement must be zero for zero current.
To model a linear motor with a repeated flux pattern, set the Flux
dependence on displacement parameter to
Cyclic. When selecting this option, the
force and flux (or force and flux partial derivatives depending on the
option chosen) must have identical first and last columns.
Note
The actuated motion direction of this block can be swapped by flipping the block and swapping the R and C connections.
Model Thermal Effects
You can expose the thermal port to model the effects of losses that convert power to heat. To expose the thermal port, set the Modeling option parameter to either:
No thermal port— The block does not contain a thermal port.Show thermal port— The block contains one thermal conserving port.
For more information about using thermal ports in actuator blocks, see Simulating Thermal Effects in Rotational and Translational Actuators.
Examples
Assumptions and Limitations
You must supply a consistent set of force and flux data. There is no check that ensures that the force matrix is consistent with the flux data.
When driving the FEM-Parameterized Linear Actuator block via a series inductor, you may need to include a parallel conductance in the inductor component.
Ports
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2010a