Choosing Identified Plant Structure
PID Tuner provides two types of model structures for representing the plant dynamics: process models and state-space models.
Use your knowledge of system characteristics and the level of accuracy required by your application to pick a model structure. In absence of any prior information, you can gain some insight into the order of dynamics and delays by analyzing the experimentally obtained step response and frequency response of the system. For more information see the following in the System Identification Toolbox™ documentation:
Correlation Models (System Identification Toolbox)
Frequency-Response Models (System Identification Toolbox)
Each model structure you choose has associated dynamic elements, or model parameters. You adjust the values of these parameters manually or automatically to find an identified model that yields a satisfactory match to your measured or simulated response data. In many cases, when you are unsure of the best structure to use, it helps to start with the simplest model structure, transfer function with one pole. You can progressively try identification with higher-order structures until a satisfactory match between the plant response and measured output is achieved. The state-space model structure allows an automatic search for optimal model order based on an analysis of the input-output data.
When you begin the plant identification task, a transfer function model structure with one real pole is selected by default. This default set up is not sensitive to the nature of the data and may not be a good fit for your application. It is therefore recommended that you choose a suitable model structure before performing parameter identification.
Process Models
Process models are transfer functions with 3 or fewer poles, and can be augmented by addition of zero, delay and integrator elements. Process models are parameterized by model parameters representing time constants, gain, and time delay. In PID Tuner, choose a process model in the Plant Identification tab using the Structure menu.

For any chosen structure you can optionally add a delay, a zero and/or an integrator element using the corresponding checkboxes. Click Edit Parameters to view the model transfer function configured by these choices.
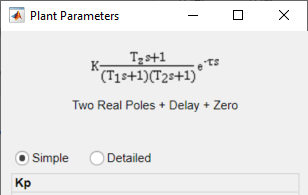
The simplest available process model is a transfer function with one real pole and no zero or delay elements:
This model is defined by the parameters K, the gain, and T1, the first time constant. The most complex process-model structure choose has three poles, an additional integrator, a zero, and a time delay, such as the following model, which has one real pole and one complex conjugate pair of poles:
In this model, the configurable parameters include the time constants associated with the poles and the zero, T1, Tω, and Tz. The other parameters are the damping coefficient ζ, the gain K, and the time delay τ.
When you select a process model type, PID Tuner automatically computes initial values for the plant parameters and displays a plot showing both the estimated model response and your measured or simulated data. You can edit the parameter values graphically using indicators on the plot, or numerically using the Plant Parameters editor. For an example illustrating this process, see Interactively Estimate Plant Parameters from Response Data.
The following table summarizes the various parameters that define the available types of process models.
| Parameter | Used By | Description |
|---|---|---|
| K — Gain | All transfer functions | Can take any real value. In the plot, drag the plant response curve (blue) up or down to adjust K. |
| T1 — First time constant | Transfer function with one or more real poles | Can take any value between 0 and T, the time span of measured or simulated data. In the plot, drag the red x left (towards zero) or right (towards T) to adjust T1. |
| T2— Second time constant | Transfer function with two real poles | Can take any value between 0 and T, the time span of measured or simulated data. In the plot, drag the magenta x left (towards zero) or right (towards T) to adjust T2. |
| Tω — Time constant associated with the natural frequency ωn, where Tω = 1/ωn | Transfer function with underdamped pair (complex conjugate pair) of poles | Can take any value between 0 and T, the time span of measured or simulated data. In the plot, drag one of the orange response envelope curves left (towards zero) or right (towards T) to adjust Tω. |
| ζ — Damping coefficient | Transfer function with underdamped pair (complex conjugate pair) of poles | Can take any value between 0 and 1. In the plot, drag one of the orange response envelope curves left (towards zero) or right (towards T) to adjust ζ. |
| τ — Transport delay | Any transfer function | Can take any value between 0 and T, the time span of measured or simulated data. In the plot, drag the orange vertical bar left (towards zero) or right (towards T) to adjust τ. |
| Tz — Model zero | Any transfer function | Can take any value between –T and T, the time span of measured or simulated data. In the plot, drag the red circle left (towards –T) or right (towards T) to adjust Tz. |
| Integrator | Any transfer function | Adds a factor of 1/s to the transfer function. There is no associated parameter to adjust. |
State-Space Models
The state-space model structure for identification is primarily defined by the choice of number of states, the model order. Use the state-space model structure when higher order models than those supported by process model structures are required to achieve a satisfactory match to your measured or simulated I/O data. In the state-space model structure, the system dynamics are represented by the state and output equations:
x is a vector of state variables, automatically chosen by the software based on the selected model order. u represents the input signal, and y the output signals.
To use a state-space model structure, in the Plant Identification tab,
in the Structure menu, select State-Space Model.
Then click Configure Structure to open the State-Space Model
Structure dialog box.

Use the dialog box to specify model order, delay and feedthrough characteristics. If you are unsure about the order, select Pick best value in the range, and enter a range of orders. In this case, when you click Estimate in the Plant Estimation tab, the software displays a bar chart of Hankel singular values. Choose a model order equal to the number of Hankel singular values that make significant contributions to the system dynamics.
When you choose a state-space model structure, the identification plot shows a plant response (blue) curve only if a valid estimated model exists. For example, if you change structure after estimating a process model, the state-space equivalent of the estimated model is displayed. If you change the model order, the plant response curve disappears until a new estimation is performed.
When using the state-space model structure, you cannot directly interact with the model parameters. The identified model should thus be considered unstructured with no physical meaning attached to the state variables of the model.
However, you can graphically adjust the input delay and the overall gain of the model. When you select a state-space model with a time delay, the delay is represented on the plot by a vertical orange bar is shown on the plot. Drag this bar horizontally to change the delay value. Drag the plant response (blue) curve up and down to adjust the model gain.
Existing Plant Models
Any previously imported or identified plant models are listed the Plant List area.

You can define the model structure and initialize the model parameter values using one of these plants. To do so, in the Plant Identification tab, in the Structure menu, select a linear plant model.

If the plant you select is a process model (idproc (System Identification Toolbox) object), PID Tuner uses its structure for the identified plant. If
the plant is any other model type, PID Tuner uses the state-space model structure. The
app initializes the estimated plant parameters using the selected plant.
Switching Between Model Structures
When you switch from one model structure to another, the software preserves the model characteristics (pole/zero locations, gain, delay) as much as possible. For example, when you switch from a one-pole model to a two-pole model, the existing values of T1, Tz, τ and K are retained, T2 is initialized to a default (or previously assigned, if any) value.
Estimating Parameter Values
Once you have selected a model structure, you have several options for manually or automatically adjusting parameter values to achieve a good match between the estimated model response and your measured or simulated input/output data. For an example that illustrates all these options, see:
Interactively Estimate Plant Parameters from Response Data (Control System Toolbox™)
Interactively Estimate Plant from Measured or Simulated Response Data Simulink® Control Design™)
PID Tuner does not perform a smart initialization of model parameters when a model structure is selected. Rather, the initial values of the model parameters, reflected in the plot, are arbitrarily-chosen middle of the range values. If you need a good starting point before manually adjusting the parameter values, use the Initialize and Estimate option from the Plant Identification tab.
Handling Initial Conditions
In some cases, the system response is strongly influenced by the initial conditions. Thus a description of the input to output relationship in the form of a transfer function is insufficient to fit the observed data. This is especially true of systems containing weakly damped modes. PID Tuner allows you to estimate initial conditions in addition to the model parameters such that the sum of the initial condition response and the input response matches the observed output well. Use the Estimation Options dialog box to specify how the initial conditions should be handled during automatic estimation. By default, the initial condition handling (whether to fix to zero values or to estimate) is automatically performed by the estimation algorithm. However, you can enforce a certain choice by using the Initial Conditions menu.
Initial conditions can only be estimated with automatic estimation. Unlike the model parameters, they cannot be modified manually. However, once estimated they remain fixed to their estimated values, unless the model structure is changed or new identification data is imported.
If you modify the model parameters after having performed an automatic estimation, the model response will show a fixed contribution (i.e., independent of model parameters) from initial conditions. In the following plot, the effects of initial conditions were identified to be particularly significant. When the delay is adjusted afterwards, the portion of the response to the left of the input delay marker (the τ Adjustor) comes purely from initial conditions. The portion to the right of the τ Adjustor contains the effects of both the input signal as well as the initial conditions.
