Model a Continuous System
To model the differential equation
x´= –2x(t)+u(t),
where u(t) is a square wave with an amplitude of
1 and a frequency of 1 rad/sec, use an integrator
block and a gain block. The Integrator block integrates its input x´ to produce
x. Other blocks needed in this model include a Gain block and a Sum
block. To generate a square wave, use a Signal Generator block and select the Square Wave form
but change the default units to radians/sec. Again, view the output using a Scope block.
Gather the blocks and define the gain.
In this model, to reverse the direction of the Gain block, select the block, then
on the Format tab, click Flip left-right ![]() . To create the branch line from the output of the Integrator
block to the Gain block, hold down the Ctrl key while drawing
the line. For more information, see Connect Single Output Port to Multiple Input Ports.
. To create the branch line from the output of the Integrator
block to the Gain block, hold down the Ctrl key while drawing
the line. For more information, see Connect Single Output Port to Multiple Input Ports.
Now you can connect all the blocks.

An important concept in this model is the loop that includes the Sum block, the Integrator block, and the Gain block. In this equation, x is the output of the Integrator block. It is also the input to the blocks that compute x´, on which it is based. This relationship is implemented using a loop.
The Scope displays x at each time step. For a simulation lasting 10 seconds, the output looks like this:

The equation you modeled in this example can also be expressed as a transfer function. The model uses the Transfer Fcn block, which accepts u as input and outputs x. So, the block implements x/u. If you substitute sx for x´ in the above equation, you get
sx = –2x + u.
Solving for x gives
x = u/(s + 2)
or,
x/u = 1/(s + 2).
The Transfer Fcn block uses parameters to specify the numerator and
denominator coefficients. In this case, the numerator is 1 and the
denominator is s+2. Specify both terms as vectors of coefficients of
successively decreasing powers of s.
In this case the numerator is [1] (or just 1) and
the denominator is [1 2].
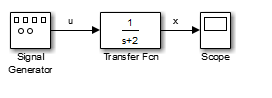
The results of this simulation are identical to those of the previous model.