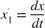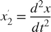Van der Pol Oscillator
This example shows how to model the second-order Van der Pol (VDP) differential equation in Simulink®. In dynamics, the VDP oscillator is non-conservative and has nonlinear damping. At high amplitudes, the oscillator dissipates energy. At low amplitudes, the oscillator generates energy. The oscillator is given by this second-order differential equation:
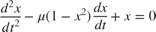
where:
x is position as a function of time.
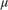 is damping.
is damping.
To express the second-order differential equation in state-space format, define  . This state-space representation is included in the model as
. This state-space representation is included in the model as 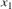 and
and 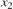 .
.
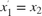
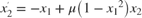
where :
The VDP oscillator is used in physical and biological sciences, including electric circuits.
open_system('vdp');

Simulate with Mu = 1
When 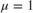 , the VDP oscillator has nonlinear damping.
, the VDP oscillator has nonlinear damping.
set_param('vdp/Mu','Gain','1') sim('vdp'); open_system('vdp/Scope');

Simulate with Mu = 0
When 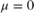 , the VDP oscillator has no damping. Energy is conserved in this simple harmonic oscillator. The equation becomes:
, the VDP oscillator has no damping. Energy is conserved in this simple harmonic oscillator. The equation becomes:

set_param('vdp/Mu','Gain','0') sim('vdp'); open_system('vdp/Scope');

See Also
Topics
- Real-Time Van der Pol Simulation (Simulink Desktop Real-Time)
- Model Differential Algebraic Equations
References
[1] Cartwright, M. L. "Balthazar Van Der Pol." Journal of the London Mathematical Society. Wiley. s1 35 (July 1960): 367–376. https://doi:10.1112/jlms/s1-35.3.367.
[2] Hirsch, Morris W., Stephen Smale, Robert L. Devaney, and Morris W. Hirsch. Differential Equations, Dynamical Systems, and an Introduction to Chaos. 2nd Ed. San Diego: Academic Press, 2004.