Simulate a Sample-and-Hold System
This example shows several ways to simulate the output of a sample-and-hold system by upsampling and filtering a signal.
Construct a sinusoidal signal. Specify a sample rate such that 16 samples correspond to exactly one signal period. Draw a stem plot of the signal. Overlay a stairstep graph for sample-and-hold visualization.
fs = 16; t = 0:1/fs:1-1/fs; x = .9*sin(2*pi*t); stem(t,x) hold on stairs(t,x) hold off

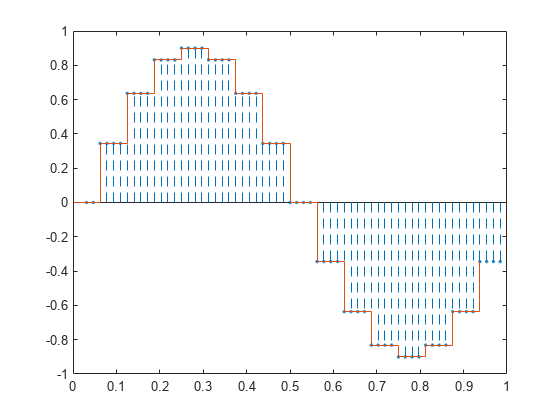
Upsample the signal by a factor of four. Plot the result alongside the original signal. upsample increases the sample rate of the signal by adding zeros between the existing samples.
ups = 4; fu = fs*ups; tu = 0:1/fu:1-1/fu; y = upsample(x,ups); stem(tu,y,'--x') hold on stairs(t,x) hold off
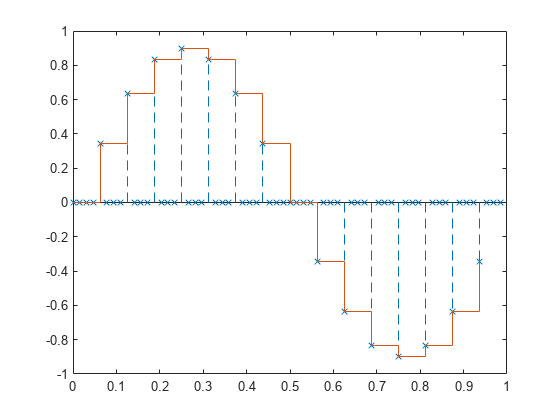
Filter with a moving-average FIR filter to fill in the zeros with sample-and-hold values.
h = ones(ups,1); z = filter(h,1,y); stem(tu,z,'--.') hold on stairs(t,x) hold off

You can obtain the same behavior using the MATLAB® function interp1 with nearest-neighbor interpolation. In that case, you must shift the origin to line up the sequence.
zi = interp1(t,x,tu,'nearest'); dl = floor(ups/2); stem(tu(1+dl:end),zi(1:end-dl),'--.') hold on stairs(t,x) hold off

The function resample produces the same result when you set the last input argument to zero.
q = resample(x,ups,1,0); stem(tu(1+dl:end),q(1:end-dl),'--.') hold on stairs(t,x) hold off