Find Periodicity Using Frequency Analysis
It is often difficult to characterize oscillatory behavior in data by looking at time measurements. Spectral analysis can help determine if a signal is periodic and measure the different cycles.
A thermometer in an office building measures the inside temperature every half hour for four months. Load the data and plot it. Convert the temperature to degrees Celsius. Measure time in weeks. The sample rate is thus 2 measurements/hour × 24 hours/day × 7 days/week = 336 measurements/week.
load officetemp tempC = (temp - 32)*5/9; fs = 2*24*7; t = (0:length(tempC) - 1)/fs; plot(t,tempC) xlabel('Time (weeks)') ylabel('Temperature ( {}^\circC )') axis tight

The temperature does seem to oscillate, but the lengths of the cycles cannot be determined easily. Look at the signal's frequency content instead.
Subtract the mean to concentrate on temperature fluctuations. Compute and plot the periodogram.
tempnorm = tempC - mean(tempC); [pxx,f] = periodogram(tempnorm,[],[],fs); plot(f,pxx) ax = gca; ax.XLim = [0 10]; xlabel('Frequency (cycles/week)') ylabel('Magnitude')
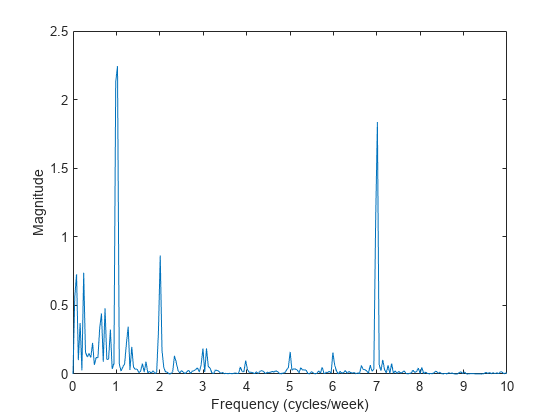
The temperature clearly has a daily cycle and a weekly cycle. The result is not surprising: the temperature is higher when people are at work and lower at nights and on weekends.
See Also
findpeaks | periodogram | xcorr