Design and Analyze Savitzky-Golay Filters
This example shows how to design, analyze, and apply Savitzky-Golay smoothing and differentiation filters to sampled signals with additive noise. The example also shows you how to use a weighting vector to optimize the frequency response and improve smoothness.
Savitzky-Golay Filters
Savitzly-Golay (SG) filters [1] are digital FIR lowpass filters that operate by moving least-squares polynomial fitting to input data samples within an interval. You can use SG filters to smooth or differentiate signal data, aiming to reduce noise while preserving the overall shape of the signal. This code creates and smooths a noisy Gaussian peak signal by performing SG filtering.
rng default
s = generateGaussianPeaks((0:999)',500,500);
s = s + 0.1*randn(size(s));
plot([s sgolayfilt(s,3,301)])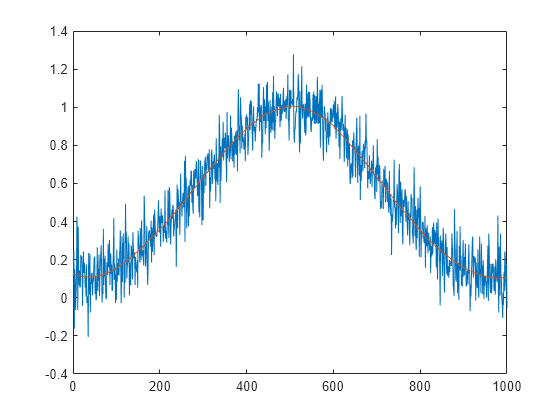
Filter Design
SG filters are typically characterized by these parameters:
: Filter polynomial order, which is the degree of the lest-squares fitted polynomials used in the filter.
: Frame length, which is the number of signal samples that form the interval width around the sample being filtered. Alternatively, the half-width interval can also characterize SG filters, where .
Design an SG filter using 6th-order polynomials and with the half width of 50 samples. Return the first differentiation filter.
m = 6; nh = 50; fl = 2*nh+1; [~,gSG] = sgolay(m,fl); gSG = gSG(:,1);
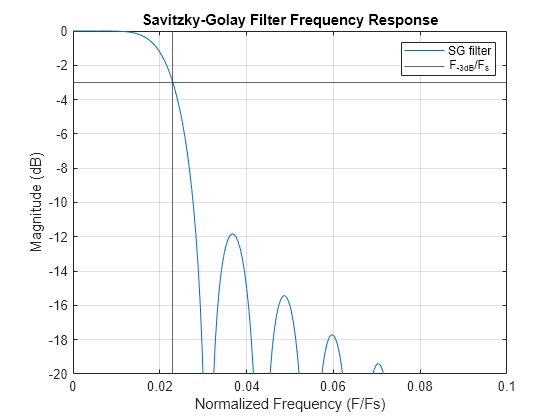
Designing SG filters based on their cutoff frequency involves following guidelines that aim to provide a good approximation in the frequency response. Schmid et. al [2] propose a relation between the cutoff frequency [1] and the SG filter characteristic parameters (). For a filter order , filter half width , and a sample rate , the 3 dB cutoff frequency is
.
This expression, obtained from least-squares fitting, is a good approximation for .
Compute the cutoff frequency for the SG filter using a sample rate of 1000 Hz.
Fs = 1000;
F3dB = Fs/(6.352*(nh+1/2)/(m+1.379) - ...
(0.513+0.316*m)/(nh+1/2));
disp(F3dB/Fs)0.0230
Compute the frequency response of the SG filter using 1024 DFT points. Plot the magnitude of the frequency response. Zoom in for the highest 20 dB of magnitude and up to 0.1 times the sample rate. The expression accurately approximates the cutoff frequency for the designed filter gSG.
NDFT = 1024; [HSG,F] = freqz(gSG,1,NDFT,Fs); figure plot(F/Fs,mag2db(abs(HSG))) xline(F3dB/Fs) yline(-3) title("Savitzky-Golay Filter Frequency Response") xlabel("Normalized Frequency (F/Fs)") ylabel("Magnitude (dB)") legend(["SG filter" "F_{-3dB}/F_s"]) axis([0 0.1 -20 0]) grid on
Weighting Vector in Savitzky-Golay Filters
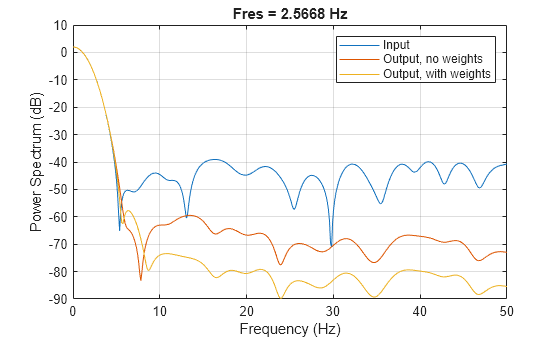
You can use a weighting vector in SG filters to optimize the frequency response by further reducing the high-frequency components.
pspectrum([s sgolayfilt(s,3,301) sgolayfilt(s,3,301,hamming(301))],Fs) legend(["Input" "Output, no weights" "Output, with weights"]) xlim([0 0.1*Fs/2])
Analytical expressions provide a relation between filter characteristics and filter response. You can use these expressions when designing SG filters with weights. For instance, the half-width half magnitude of an SG filter with weights, which has the same normalized cutoff frequency as the regular SG filter without weighting, is given by this expression [2]:
.
This expression is based on least-squares fitting and connects with the half-width interval . The suffix in denotes the use of a weighting vector. Using weighting vectors when designing SG filters results in a wider half-magnitude interval, nhW, compared to nh.
nhW = round((0.509+0.1922*m-0.001485*m^2)/(F3dB/Fs)-1); disp(table([nh;nhW],VariableNames="Value",RowNames=["nh";"nhW"]))
Value
_____
nh 50
nhW 69
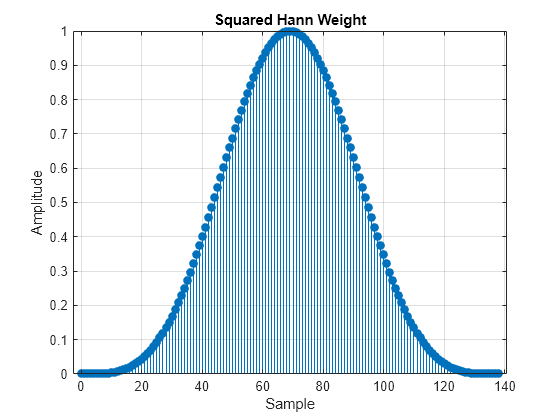
Design a squared Hann window. The sgolay function does not accept zeros in the weighting vector argument. Ensure that all the samples are positive numbers. Plot the window.
flW = 2*nhW+1; weightsSqHann = hann(flW+2).^2; weightsSqHann([1 end]) = []; figure stem(0:flW-1,weightsSqHann,"filled") title("Squared Hann Weight") xlabel("Sample") ylabel("Amplitude") grid on
Design an SG filter using squared Hann weights. Return the first differentiation filter and compute its frequency response.
[~,gSGwSqHann] = sgolay(m,flW,weightsSqHann); gSGwSqHann = gSGwSqHann(:,1); HSGwSqHann = freqz(gSGwSqHann,1,NDFT,Fs);
Effect of Weighting in Savitzky-Golay Filters
To observe the impact of weighting on the SG filter design, compare the filter impulse and frequency responses.
Filter Impulse Response
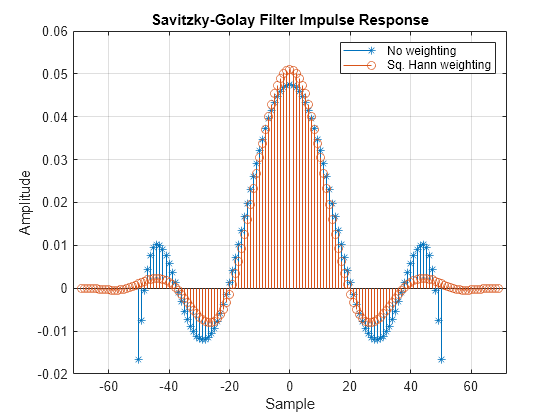
Plot the impulse response for the SG filters without weighting (gSG) and with squared-Hann weighting (gSGwSqHann). Compare the impulse responses by using a symmetric x-axis. Observe that adding a weighting vector in the SG filter redistributes the amplitudes, reducing sidelobes while taking a longer duration to reach the zero-value steady response.
figure stem(-nh:nh,gSG,"*") hold on stem(-nhW:nhW,gSGwSqHann) hold off title("Savitzky-Golay Filter Impulse Response") xlabel("Sample") ylabel("Amplitude") legend(["No weighting" "Sq. Hann weighting"]) grid on
Filter Frequency Response
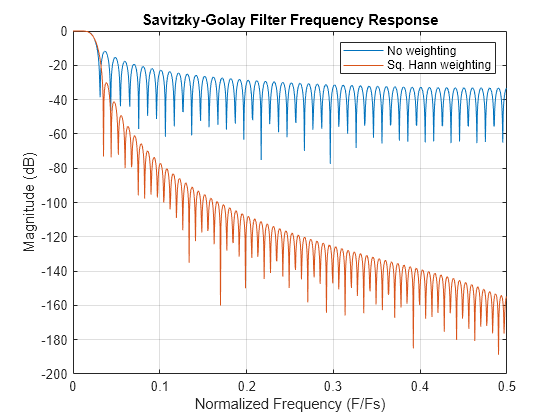
Plot the magnitude of the frequency response for the SG filters without weighting (HSG) and with squared Hann weighting (HSGwSqHann). Use the sample rate to normalize the frequency on the x-axis. Compare the frequency responses. Observe that adding a weighting vector in the SG filter significantly reduces the noise at frequencies above the cutoff frequency.
figure plot(F/Fs,mag2db(abs(HSG)),F/Fs,mag2db(abs(HSGwSqHann))) title("Savitzky-Golay Filter Frequency Response") xlabel("Normalized Frequency (F/Fs)") ylabel("Magnitude (dB)") legend(["No weighting" "Sq. Hann weighting"]) grid on
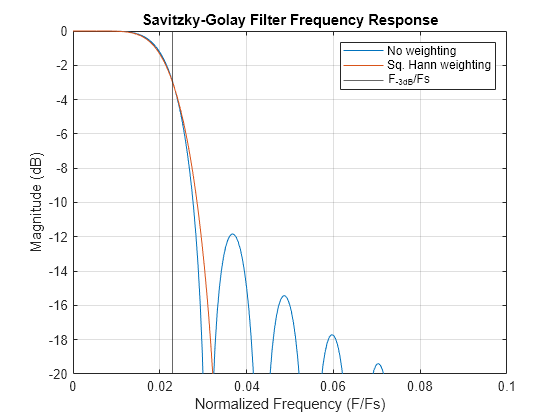
Zoom in for the highest 20 dB of magnitude and up to 0.1 times the sample rate. The half-magnitude cutoff frequency for the SG filter with squared Hann weighting remains unchanged at approximately 0.023 times the sample rate. Even though SG filters with weighting require a larger order to achieve the same cutoff frequency, the frequency response shows an enhanced attenuation of unwanted frequencies.
xline(F3dB/Fs) title("Savitzky-Golay Filter Frequency Response") xlabel("Normalized Frequency (F/Fs)") ylabel("Magnitude (dB)") legend(["No weighting" "Sq. Hann weighting" "F_{-3dB}/Fs"]) axis([0 0.1 -20 0]) grid on
Optimal Weights with Optimal Smoothness
Weighting vectors in SG filters reduce more noise in signals as compared to SG filters that do not use weighting. As an added benefit, you can achieve optimal smoothness by choosing optimal weights during the design of SG filters.
Optimal Weighting Formulation
Consider the input signal , modeled as , where is the signal component without noise, is an independent and identically distributed (IID) noise signal component with a variance , and counts the samples along these signals. Filtering yields the output signal :
,
where and .
The output vs. input noise ratio is defined as
The output noise is considered to be smooth to the extent that the difference between successive values of the output noise, , is small.
One way to quantify smoothness is to use the ratio of noise energy between consecutive samples at the filter output to the noise energy between consecutive samples at the filter input. Assuming that the noise is IID, the smoothness is given by
The output gets smoother as gets smaller.
By construction, the weight sequence that minimizes is a quadratic function.
If the column vector and the -by- Toeplitz matrix are expressed as:
,
Then . The optimal weights are given by , , where and .
Filter Design with Optimal Weighting Vector
To illustrate SG filtering with optimal weights and compare with other weights, this example uses the half-magnitude half width for SG filters with weighting, , calculated in the Weighting Vector in Savitzky-Golay Filters section. Therefore, the number of frames to use in this design is nFramesW.
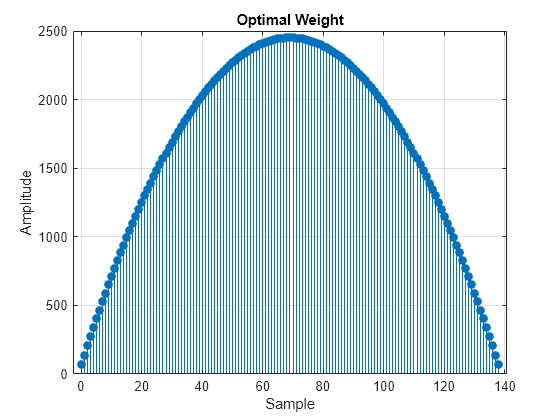
Design an optimal weighting vector based on the quadratic function formulation. Plot the window.
Tn = toeplitz([2 -1 zeros(1,flW-2)]); v = ones(flW,1); weightsOptimal = Tn\v; figure stem(0:flW-1,weightsOptimal,"filled") title("Optimal Weight") xlabel("Sample") ylabel("Amplitude") grid on
Design an SG filter with the optimal weighting vector weightsOptimal and nFramesW frames. Compute the frequency response, output vs. input noise ratio, and smoothness.
[~,gSGwOptimal] = sgolay(m,flW,weightsOptimal); gSGwOptimal = gSGwOptimal(:,1); HSGwOptimal = freqz(gSGwOptimal,1,NDFT,Fs);
Calculate the output vs. input noise ratio and the smoothness for the SG filter with optimal weighting.
rSGwOptimal = gSGwOptimal'*gSGwOptimal; sSGwOptimal = diff([0;gSGwOptimal;0]); sSGwOptimal = sum(abs(sSGwOptimal).^2)/2;
Effect of Optimal Weighting in Savitzky-Golay Filters
To compare the effect of optimal weighting, this example analyzes the frequency response of the SG filters with these weighting strategies: none, squared Hann, triangular, and optimal.
Design an SG filter without weighting with nFramesW frames. Compute the frequency response.
[~,gSGwNone] = sgolay(m,flW); gSGwNone = gSGwNone(:,1); HSGwNone = freqz(gSGwNone,1,NDFT,Fs);
Calculate the output vs. input noise ratio and the smoothness for the SG filter without weighting, gSGwNone.
rSGwNone = gSGwNone'*gSGwNone; sSGwNone = diff([0;gSGwNone;0]); sSGwNone = sum(abs(sSGwNone).^2)/2;
Calculate the output vs. input noise ratio and the smoothness for the SG filter with square Hann weighting, gSGwSqHann.
rSGwSqHann = gSGwSqHann'*gSGwSqHann; sSGwSqHann = diff([0;gSGwSqHann;0]); sSGwSqHann = sum(abs(sSGwSqHann).^2)/2;
Design an SG filter with triangular weighting and nFramesW frames. Compute the frequency response, output vs. input noise ratio, and smoothness. As described in Turton [3], triangular weighting improves the frequency response of SG filters.
weightsTriang = triang(flW); [~,gSGwTriang] = sgolay(m,flW,weightsTriang); gSGwTriang = gSGwTriang(:,1); HSGwTriang = freqz(gSGwTriang,1,NDFT,Fs); rSGwTriang = gSGwTriang'*gSGwTriang; sSGwTriang = diff([0;gSGwTriang;0]); sSGwTriang = sum(abs(sSGwTriang).^2)/2;
To observe the impact of optimal weighting on SG filters, compare the output vs. input noise ratios, smoothness, and the filter impulse and frequency responses.
Noise Reduction and Smoothness
Display a table with the output vs. input noise ratios, , and smoothness parameter values, , for the four SG filters. Observe that the smoothness improves for SG filters with weighting vectors, at the cost of slightly less noise reduction. The filter with optimal weighting also provides the best smoothness.
disp(table(["None";"Sq. Hann";"Triangular";"Optimal"], ... db([rSGwNone;rSGwSqHann;rSGwTriang;rSGwOptimal]), ... db([sSGwNone;sSGwSqHann;sSGwTriang;sSGwOptimal]), ... VariableNames=["Weighting" ... "Output/Input Noise Ratio (dB)" "Smoothness (dB)"]))
Weighting Output/Input Noise Ratio (dB) Smoothness (dB)
____________ _____________________________ _______________
"None" -29.258 -70.13
"Sq. Hann" -26.815 -75.17
"Triangular" -28.526 -79.955
"Optimal" -28.822 -80.513
Filter Impulse Response
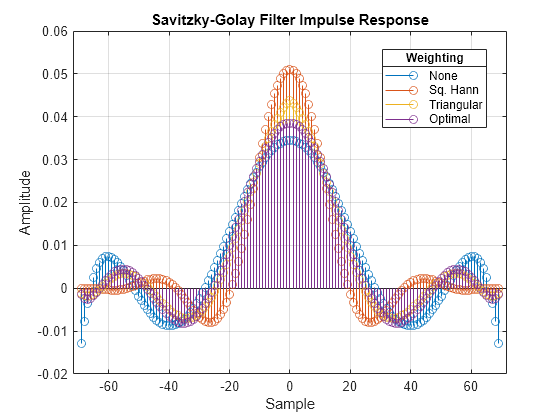
Plot the impulse response for the four SG filters. Compare the impulse responses by using a symmetric x-axis. Observe that using the quadratic-function optimal weighting vector in the SG filter redistributes the amplitudes as well as with the other vectors, with a more balanced increase in the peak at the main lobe while maintaining low sidelobes levels.
figure stem(-nhW:nhW,[gSGwNone gSGwSqHann gSGwTriang gSGwOptimal]) title("Savitzky-Golay Filter Impulse Response") xlabel("Sample") ylabel("Amplitude") lgn = legend(["None" "Sq. Hann" "Triangular" "Optimal"], ... Location="best"); title(lgn,"Weighting") grid on
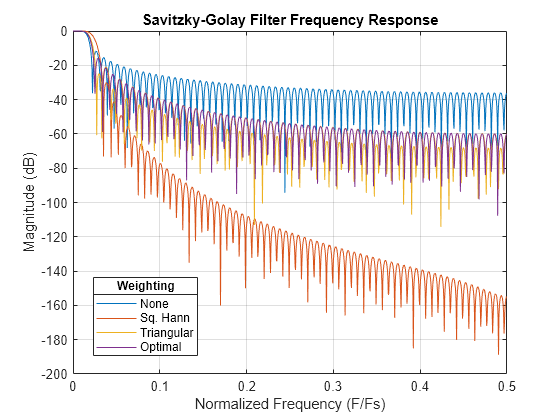
Filter Frequency Response
Plot the magnitude of the frequency response for the SG filters without weighting (HSG) and with the squared Hann weighting (HSGwSqHann). Use the sample rate to normalize the frequency on the x-axis. Compare the frequency responses. Observe that the SG filter with the optimal weighting vector produces a significant noise reduction at frequencies above the cutoff frequency, even though the magnitude attenuates at a slower slope over the frequency range.
figure plot(F/Fs,mag2db(abs( ... [HSGwNone HSGwSqHann HSGwTriang HSGwOptimal]))) title("Savitzky-Golay Filter Frequency Response") xlabel("Normalized Frequency (F/Fs)") ylabel("Magnitude (dB)") lgn = legend(["None" "Sq. Hann" "Triangular" "Optimal"], ... Location="best"); title(lgn,"Weighting") grid on
Filter Noisy Gaussian Peak Sequence
You can apply SG filtering to noisy signals to smooth or differentiate them. This example smooths a noisy sequence of Gaussian peaks using SG filtering.
Generate Gaussian Peak Sequence
Design a sequence of three Gaussian peaks with these specifications:
The first peak occurs at a time seconds.
The full-width half-maximum (FWHM) width of the first peak, , is 3.2 seconds.
The FWHM ratio between consecutive peaks is .
nPeaks = 3;
tp1 = 10;
wp1 = 3.2;
alpha = 1/log(2);
wp = wp1./alpha.^(0:nPeaks-1);
tp = tp1+2*cumsum([0 wp(1:nPeaks-1)+wp(2:nPeaks)]);
% Gaussian peak sequence
t = (0:1/Fs:tp(end)+5*wp(end))';
u = generateGaussianPeaks(t,tp,wp);See Appendix: Helper Function for more information about the generateGaussianPeaks function.
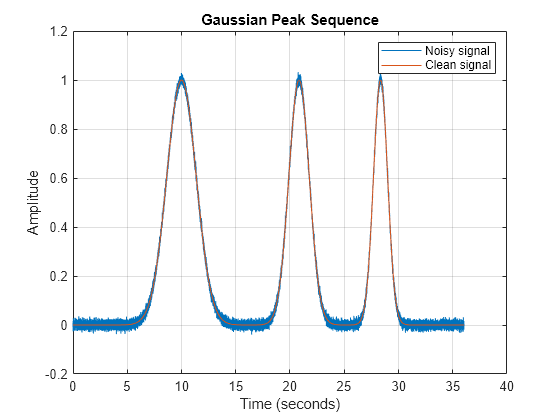
Add normally-distributed noise to the peaks with standard deviation . Plot a comparison of the clean and noisy sequence of Gaussian peaks.
sd = 0.01; noise = sd*randn(size(u)); x = u + noise; figure plot(t,x,t,u) title("Gaussian Peak Sequence") xlabel("Time (seconds)") ylabel("Amplitude") legend(["Noisy" "Clean"]+ " signal") grid on
Filter Noisy Signal
Apply SG filtering to the noisy Gaussian-peaks sequence x using square Hann, triangular, and optimal weighting vectors.
ySGwSqHann = sgolayfilt(x,m,flW,weightsSqHann); ySGwTriang = sgolayfilt(x,m,flW,weightsTriang); ySGwOptimal = sgolayfilt(x,m,flW,weightsOptimal);
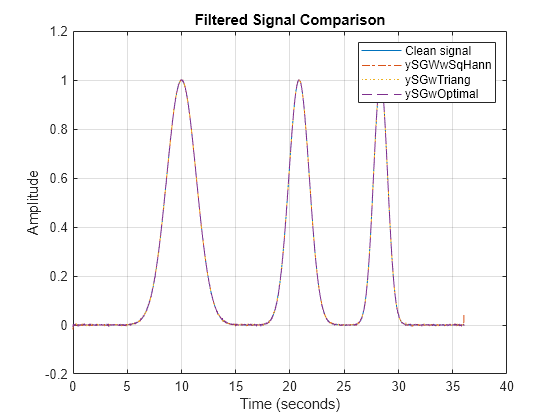
Plot the clean signal, and compare it with the filtered signals. The filtered signals closely resemble the clean signal, demonstrating effective noise removal.
figure plot(t,u) hold on plot(t,ySGwSqHann,"-.") plot(t,ySGwTriang,":") plot(t,ySGwOptimal,"--") title("Filtered Signal Comparison") xlabel("Time (seconds)") ylabel("Amplitude") legend(["Clean signal" ... "ySGWwSqHann" "ySGwTriang" "ySGwOptimal"]) grid on
Filter Performance
To further compare the effect of the weighting vectors in the SG filtering performance, this example computes the signal residues and compares them with the input noise to observe the noise reduction for each of the SG filters.
Calculate the residual signals for each SG filter, defined as the difference between the output filtered signal and the clean signal.
eSGwSqHann = ySGwSqHann-u; eSGwTriang = ySGwTriang-u; eSGwOptimal = ySGwOptimal-u;
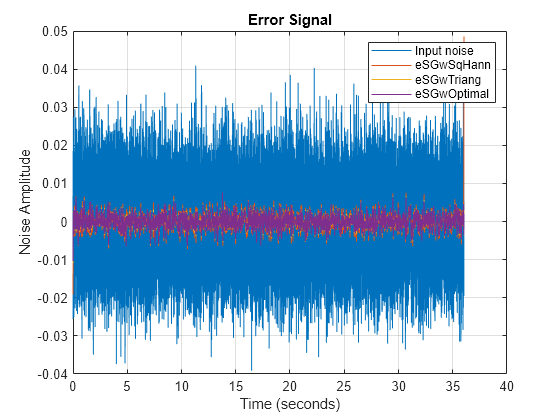
Plot the input noise and compare it with the residual signals for each SG filter. All the SG filters show lower noise levels compared with the input noise.
figure plot(t,[noise eSGwSqHann eSGwTriang eSGwOptimal]) title("Error Signal") xlabel("Time (seconds)") ylabel("Noise Amplitude") legend(["Input noise" "eSGwSqHann" "eSGwTriang" "eSGwOptimal"]) grid on
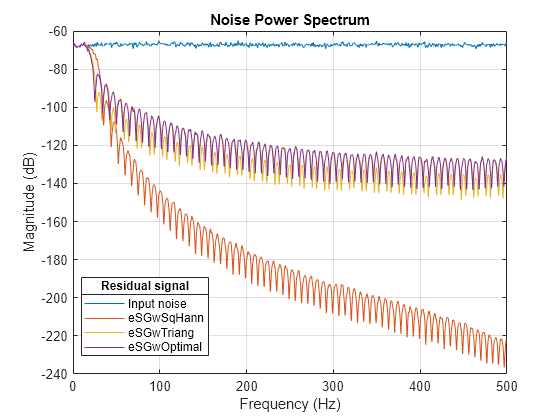
Plot the power spectrum for the input noise and for the residual signals corresponding to each SG filter. Observe that the SG filters significantly reduce signal noise. The SG filter with the optimal weighting vector produces a significant noise reduction at frequencies above the cutoff frequency, although the magnitude attenuates at a slower slope over the frequency range than with square Hann weights.
figure pspectrum([noise eSGwSqHann eSGwTriang eSGwOptimal],Fs); title("Noise Power Spectrum") xlabel("Frequency (Hz)") ylabel("Magnitude (dB)") lgn = legend(["Input noise" ... "eSGwSqHann" "eSGwTriang" "eSGwOptimal"],Location="best"); title(lgn,"Residual signal") grid on
Conclusion
This example introduces the use of Savitzky-Golay Filters using Signal Processing Toolbox™. You can use the sgolay function to design Savitzky-Golay filters for signal smoothing or differentiation. Smooth signals by applying Savitzky-Golay filters with the sgolayfilt function. You can leverage the smoothing performance by using optimal weighting vectors for a better filter performance.
References
[1] R. W. Schafer, "What Is a Savitzky-Golay Filter? [Lecture Notes]." IEEE Signal Processing Magazine, vol. 28, no. 4 (July 2011), pp. 111–117.
[2] M. Schmid, D. Rath, and U. Diebold, "Why and How Savitzky–Golay Filters Should Be Replaced." ACS Measurement Science, vol. 28, no. 4 (2022), pp. 185–196.
[3] B. C. H. Turton, "A novel variant of the Savitzky-Golay filter for spectroscopic applications." Measurement Science and Technology, vol. 3 (1992), pp. 858–863.
Appendix: Helper Function
The function listed in this section is only for use in this example and might be changed or be removed in a future release.
generateGaussianPeaks
This function creates a train of Gaussian peaks, given a time sequence t, the peak time locations tp and the corresponding full-width half-maximum time intervals wp. Specify tp and wp as row vectors with the same length.
function gPeaks = generateGaussianPeaks(t,tp,wp) gPeaks = sum(exp(-4*log(2)*((t-tp)./wp).^2),2); end
See Also
freqz | sgolay | sgolayfilt | pspectrum