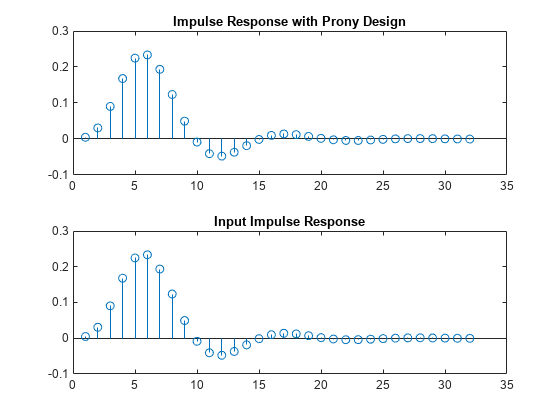
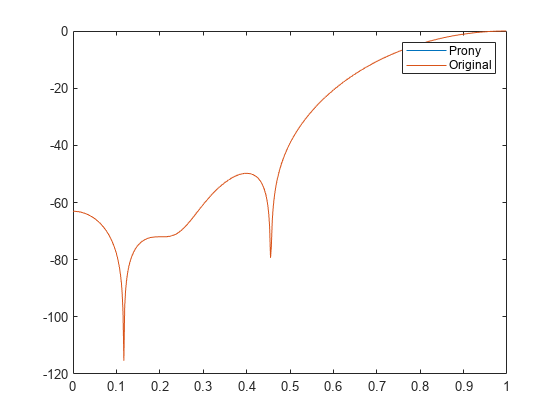
prony
Prony method for filter design
Description
Examples
Input Arguments
Output Arguments
More About
References
[1] Parks, Thomas W., and C. Sidney Burrus. Digital Filter Design. New York, NY, USA: Wiley-Interscience, 1987.
Extended Capabilities
Version History
Introduced before R2006a