enbw
Equivalent noise bandwidth
Description
Examples
Determine the equivalent noise bandwidth of a Hamming window 1000 samples in length.
bw = enbw(hamming(1000))
bw = 1.3638
Determine the equivalent noise bandwidth in Hz of a flat top window 10000 samples in length. The sample rate is 44.1 kHz.
bw = enbw(flattopwin(10000),44.1e3)
bw = 16.6285
Obtain the equivalent rectangular noise bandwidth of a 128-sample Hann window.
Generate the window and compute its discrete Fourier transform over 2048 frequencies. Shift the transform so it is centered at zero frequency and compute its squared magnitude.
lw = 128; win = hann(lw); lt = 2048; windft = fftshift(fft(win,lt)); ad = abs(windft).^2; mg = max(ad);
Specify a sample rate of 1 kHz. Use enbw to compute the equivalent noise bandwidth of the window and verify that the value coincides with the definition.
fs = 1000; bw = enbw(win,fs)
bw = 11.8110
bdef = sum((win).^2)/sum(win)^2*fs
bdef = 11.8110
Plot the squared magnitude of the window. Overlay a rectangle with height equal to the peak of the squared magnitude and width equal to the equivalent noise bandwidth.
freq = -fs/2:fs/lt:fs/2-fs/lt; plot(freq,ad, ... bw/2*[-1 -1 1 1],mg*[0 1 1 0],'--') xlim(bw*[-1 1])
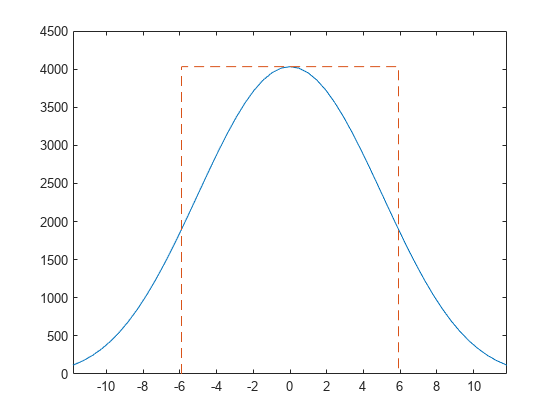
Verify that the area of the rectangle contains the same total power as the window.
Adiff = trapz(freq,ad)-bw*mg
Adiff = 1.4552e-11
Repeat the computation using normalized frequencies. Find the equivalent noise bandwidth of the window. Verify that enbw gives the same value as the definition.
bw = enbw(win)
bw = 1.5118
bdef = sum((win).^2)/sum(win)^2*lw
bdef = 1.5118
Plot the squared magnitude of the window. Overlay a rectangle with height equal to the peak of the squared magnitude and width equal to the equivalent noise bandwidth.
freqn = -1/2:1/lt:1/2-1/lt; plot(freqn,ad, ... bw/2*[-1 -1 1 1]/lw,mg*[0 1 1 0],'--') xlim(bw*[-1 1]/lw)
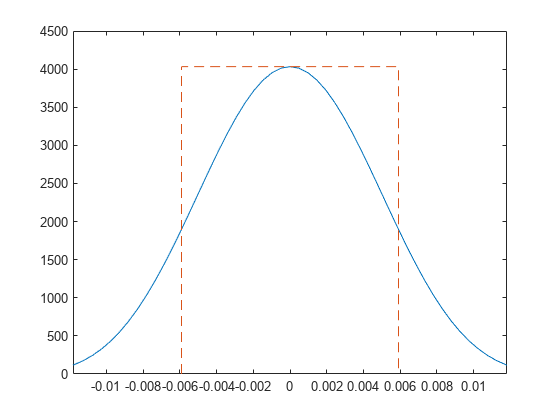
Verify that the area of the rectangle contains the same total power as the window.
Adiff = trapz(freqn,ad)-bw*mg/lw
Adiff = 1.4211e-14
Input Arguments
Uniformly sampled window vector, specified as a row or column vector with real-valued elements.
Example: hamming(1000)
Data Types: double | single
Sampling frequency, specified as a positive scalar.
Output Arguments
Equivalent noise bandwidth, specified as a positive scalar.
Data Types: double | single
More About
The total power contained in a window is the area under the curve produced by the squared magnitude of the Fourier transform of the window. The equivalent noise bandwidth of the window is the width of a rectangle with height equal to the peak of the squared magnitude of the Fourier transform and area equal to the total power.
Parseval's theorem states that the total energy for the N-sample window w(n) equals the sum of the squared magnitudes of the time-domain window samples or the integral over frequency of the squared magnitude of the Fourier transform of the window:
The power spectrum of the window has peak magnitude at f = 0:
To find the width of the equivalent rectangle, and thus the equivalent noise bandwidth, divide the area by the height:
When a sample rate fs
is specified, enbw returns the previous expression
multiplied by fs:
For normalized frequencies, the function divides by the bin width, fs/N:
See Equivalent Rectangular Noise Bandwidth for an example that, for a given window:
Compares the result of
enbwto the definition for a specified sample rate and for normalized frequencies.Plots the equivalent rectangular bandwidth over the magnitude spectrum of the window.
Verifies that the total power contained in the window is the same as the power contained in a rectangle with height equal to the peak squared magnitude of the Fourier transform of the window and width equal to the equivalent noise bandwidth.
References
[1] harris, fredric j. “On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform.” Proceedings of the IEEE®. Vol. 66, January 1978, pp. 51–83.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Version History
Introduced in R2013a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)