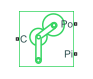
Planet-Planet
Planetary gear set of carrier, inner planet, and outer planet wheels with adjustable gear ratio and friction losses
Libraries:
Simscape /
Driveline /
Gears /
Planetary Subcomponents
Description
The Planet-Planet gear block represents a carrier and two inner-outer planet gear couples. Both planet gears are connected to and rotate with respect to the carrier. The planet gears corotate with a fixed gear ratio that you specify. For model details, see Equations.

Thermal Model
You can model
the effects of heat flow and temperature change by enabling the optional thermal port. To enable
the port, set Friction model to Temperature-dependent
efficiency.
Equations
The Planet-Planet block imposes one kinematic and one geometric constraint on the three connected axes:
The outer planet-to-inner planet gear ratio is
where N is the number of teeth on each gear. In terms of this ratio, the key kinematic constraint is
The three degrees of freedom reduce to two independent degrees of freedom. The gear pair is (1, 2) = (Pi,Po).
The torque transfer is
In the ideal case where there is no torque loss, τloss = 0.
In the nonideal case, τloss ≠ 0. For more information, see Model Gears with Losses.
Variables
Use the Variables settings to set the priority and initial target values for the block variables before simulating. For more information, see Set Priority and Initial Target for Block Variables.
Assumptions and Limitations
Gear inertia is assumed to be negligible.
Gears are treated as rigid components.
Coulomb friction slows down simulation. For more information, see Adjust Model Fidelity.
Ports
Conserving
Parameters
More About
Extended Capabilities
Version History
Introduced in R2011a