Double-Pinion Planetary Gear
Planetary gear train with two meshed planet gear sets
Libraries:
Simscape /
Driveline /
Gears
Description
The Double-Pinion Planetary Gear block represents a planetary gear train with two meshed planet gear sets between the sun gear and the ring gear. A single carrier holds the two planet gear sets at different radii from the sun gear centerline, while allowing the individual gears to rotate with respect to each other. The gear model includes power losses due to friction between meshing gear teeth and viscous damping of the spinning gear shafts.

Structurally, the double-pinion planetary gear resembles a Ravigneaux gear without its second, large, sun gear. The inner planet gears mesh with the sun gear and the outer planet gears mesh with the ring gear. Because it contains two planet gear sets, the double-pinion planetary gear reverses the relative rotation directions of the ring and sun gears.
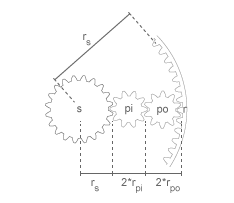
The teeth ratio of a meshed gear pair fixes the relative angular velocities of the two gears in that pair. In the Double-Pinion Planetary Gear block, you can specify the gear teeth ratios between the ring and sun gears and the outer planet and inner planet gears. A geometric constraint fixes the remaining teeth ratios—the ring gear to the outer planet gear and the inner planet gear to the sun gear. This constrains the ring gear radius to the sum of the sun gear radius and the inner and outer planet gear diameters.
where:
rr is the ring gear radius.
rs is the sun gear radius.
rpi is the inner planet gear radius.
rpo is the outer planet gear radius.
The ring to outer planet gear teeth ratio is
The inner planet-sun teeth ratio is
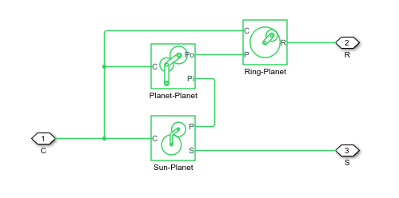
The Double-Pinion Planetary Gear block is a composite component. It contains three underlying blocks—Ring-Planet, Planet-Planet, and Sun-Planet—connected as shown in the figure. Each block connects to a separate drive shaft through a rotational conserving port.
Thermal Model
You can model
the effects of heat flow and temperature change by enabling the optional thermal port. To enable
the port, set Friction model to Temperature-dependent
efficiency.
Assumptions and Limitations
Gear inertia is assumed to be negligible.
Gears are treated as rigid components.
Coulomb friction slows down simulation. For more information, see Adjust Model Fidelity.
