Robust Stability and Worst-Case Gain of Uncertain System
This example shows how to calculate the robust stability and examine the worst-case gain of the closed-loop system described in System with Uncertain Parameters. The following commands construct that system.
m1 = ureal('m1',1,'percent',20); m2 = ureal('m2',1,'percent',20); k = ureal('k',1,'percent',20); s = zpk('s'); G1 = ss(1/s^2)/m1; G2 = ss(1/s^2)/m2; F = [0;G1]*[1 -1]+[1;-1]*[0,G2]; P = lft(F,k); C = 100*ss((s+1)/(.001*s+1))^3; T = feedback(P*C,1); % Closed-loop uncertain system
This uncertain state-space model T has three uncertain parameters, k, m1, and m2, each equal to 1±20% uncertain variation. Use robstab to analyze whether the closed-loop system T is robustly stable for all combinations of possible values of these three parameters.
[stabmarg,wcus] = robstab(T); stabmarg
stabmarg = struct with fields:
LowerBound: 2.8826
UpperBound: 2.8864
CriticalFrequency: 575.0339
The data in the structure stabmarg includes bounds on the stability margin, which indicate that the control system can tolerate almost 3 times the specified uncertainty before going unstable. It is stable for all parameter variations in the specified ±20% range. The critical frequency is the frequency at which the system is closest to instability.
The structure wcus contains the smallest destabilization perturbation values for each uncertain element.
wcus
wcus = struct with fields:
k: 1.5773
m1: 0.4227
m2: 0.4227
You can evaluate the uncertain model at these perturbation values using usubs. Examine the pole locations of that worst-case model.
Tunst = usubs(T,wcus); damp(Tunst)
Pole Damping Frequency Time Constant
(rad/seconds) (seconds)
-8.82e-01 + 1.55e-01i 9.85e-01 8.95e-01 1.13e+00
-8.82e-01 - 1.55e-01i 9.85e-01 8.95e-01 1.13e+00
-1.25e+00 1.00e+00 1.25e+00 7.99e-01
8.10e-08 + 5.75e+02i -1.41e-10 5.75e+02 -1.23e+07
8.10e-08 - 5.75e+02i -1.41e-10 5.75e+02 -1.23e+07
-1.50e+03 + 6.44e+02i 9.19e-01 1.63e+03 6.67e-04
-1.50e+03 - 6.44e+02i 9.19e-01 1.63e+03 6.67e-04
The system contains a pair of poles very close to the imaginary axis, with a damping ratio of less than 1e-7. This result confirms that the worst-case perturbation is just enough to destabilize the system.
Use wcgain to calculate the worst-case peak gain, the highest peak gain occurring within the specified uncertainty ranges.
[wcg,wcug] = wcgain(T); wcg
wcg = struct with fields:
LowerBound: 1.0474
UpperBound: 1.0731
CriticalFrequency: 7.3245
wcug contains the values of the uncertain elements that cause the worst-case gain. Compute a closed-loop model with these values, and plot its frequency response along with some random samples of the uncertain system.
Twc = usubs(T,wcug); Trand = usample(T,5); bodemag(Twc,'b--',Trand,'c:',{.1,100}); legend('Twc - worst-case','Trand - random samples','Location','SouthWest');
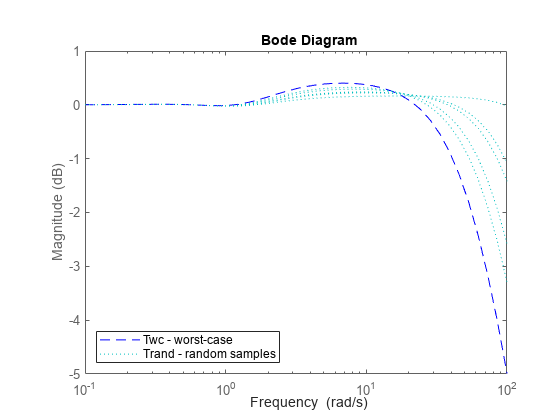
Alternatively use wcsigmaplot to visualize the highest possible gain at each frequency, the system with the highest peak gain, and random samples of the uncertain system.
wcsigmaplot(T,{.1,100})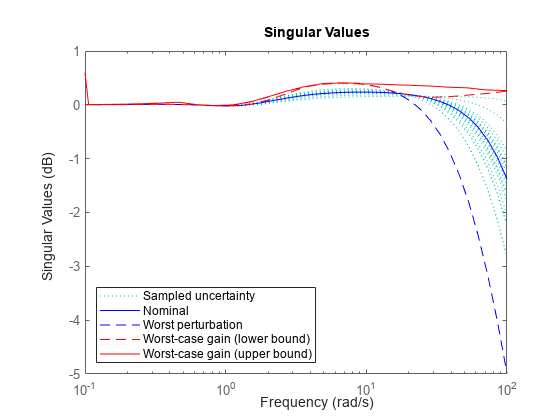
See Also
robstab | wcgain | wcsigmaplot