Surrogate Based Optimization of a Planar Spiral Inductor

This example shows you how to use an optimization based approach for designing a planar PCB spiral inductor. A surrogate optimization technique available in Global Optimization Toolbox™ is used as the optimizer. The spiral inductor material parameters and geometry gives rise to an effective inductance across the input and output ports. A rectangular spiral on a silicon substrate is chosen based on [1]. The target inductance to be achieved is 10 nH at a frequency of 3 GHz.

Define Parameters

Define units, design, and analysis parameters. Set a target inductance of 10 nH.

Hz = 1;
H = 1;
nH = 1e-9*H;
GHz = 1e9*Hz;
fc = 3*GHz;                     % Center frequency  
Ltarget = 10*nH;                % Target inductance
Z0 = 50;                        % Ref. impedance
fracBW = 0.1;                   % Fractional bandwidth
BW = fc*fracBW;                 % Absolute bandwidth
fmin = fc - 2*(BW);             % Minimum frequency
fmax = fc + 2*(BW);             % Max frequency
Nf = 50 ;                       % No. of frequency points
freq = linspace(fmin,fmax,Nf);  % Frequency points

% Populate Analysis Parameters in a struct
AnalysisParams.CenterFrequency = fc;
AnalysisParams.Bandwidth = BW;
AnalysisParams.Freq = freq;
AnalysisParams.ReferenceImpedance = 50;

Create Spiral Inductor

Use the catalog object spiralInductor to create the spiral inductor component. Assign the fixed parameters such as the groundplane dimensions, substrate material, and height. Choose the inner diameter, trace width, spacing between turns, and the number of turns as optimization variables. These four parameters are given an initial value and assigned to the appropriate properties.

% Define component to optimize
component = spiralInductor;

% Initialize component geometry and material parameters
gndL = 250e-6;
gndW = 250e-6;
h = 303e-6;
initialdesign = [70e-6,3e-6,2e-6,3];
component.InnerDiameter     = initialdesign(1);
component.Width             = initialdesign(2);
component.Spacing           = initialdesign(3);
component.NumTurns          = initialdesign(4);
component.GroundPlaneLength = gndL;
component.GroundPlaneWidth  = gndW;
component.Height = h;
d = dielectric('Name',{'Silicon','sio2'},...
               'EpsilonR',[11.9,4.1],...
               'LossTangent',[0.005,0],...
               'Thickness',[300e-6,3e-6]);
component.Substrate = d;
figure
show(component)

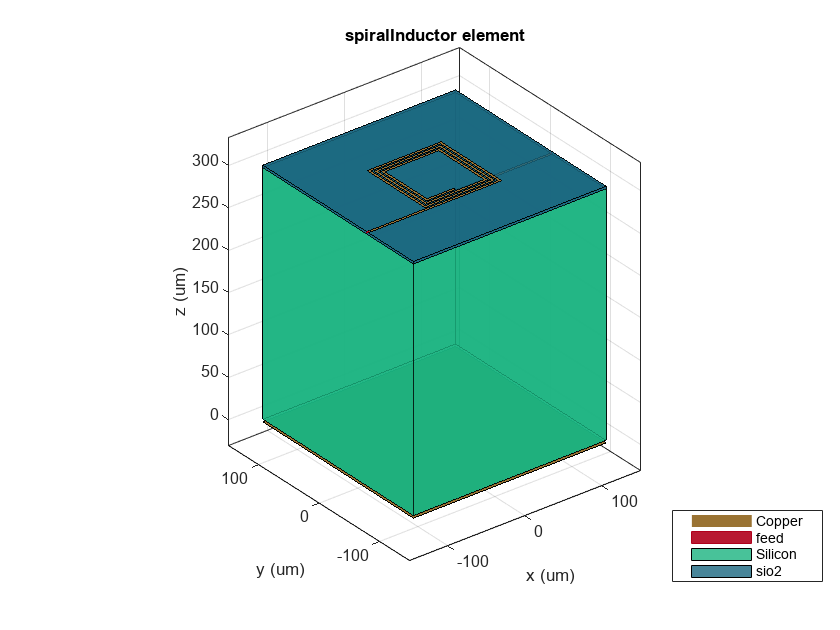
Calculate Inductance at Design Frequency

Before optimizing, calculate the inductance at the design frequency of 3 GHz

Linitial = inductance(component,fc)

Linitial = 2.1775e-09

This initial spiral inductor design does not realize the desired inductance of 10 nH at the center frequency of 3 GHz.

Set up the optimization by identifying the optimization variables and their bounds.

Set Up Optimization

The following properties are the optimization variables:

• Inner Diameter

• Width

• Spacing

• NumTurns

In terms of the list of available properties on the spiral inductor identify the indices of the four listed optimization variables. Decide and assign the lower and upper bounds on the search space for each optimization variable. The 4th property in the list, NumTurns can only take on integer values and the optimizer handles it as an integer constraint.

% Get all design variables
designVars = getObjectProperties(component)

designVars = 10×1 cell
    {'SpiralShape'      }
    {'InnerDiameter'    }
    {'Width'            }
    {'Spacing'          }
    {'NumTurns'         }
    {'Height'           }
    {'GroundPlaneLength'}
    {'GroundPlaneWidth' }
    {'Substrate'        }
    {'Conductor'        }

% Indices array into designVars to identify optim variables
optimVarIndx = [2,3,4,5];
% Lower and Upper bound for optimization on optim variables
optimVarBounds = [70e-6 90e-6;...               % InnerDiameter
                  4e-6 8e-6;...                 % Width 
                  2e-6 6e-6;...                 % Spacing
                  3 9];                         % NumTurns - Integer only
IntConstr = [0,0,0,1];                          % Identify which of the optim variables have integer contraints
% Create Design variable and Optimization Variable data structure
Design.Component = component;
Design.Variables = designVars;
Design.OptimVarIndx = optimVarIndx;
Design.OptimVarBounds = optimVarBounds;

Surrogate Based Optimization

The Global Optimization Toolbox™ provides a surrogate based optimization function called surrogateopt and you can use this with options specified with the optimoptions function. At every iteration, plot the best value of the objective function. Pass the objective function to the surrogateopt function by using an anonymous function together with the bounds and the options structure. You can find the objective function used by surrogateopt in the file spiralInductor_objective_function.

OptimParams = optimoptions(@surrogateopt);
OptimParams.UseParallel = true;
OptimParams.MinSampleDistance = 1e-9;
OptimParams.InitialPoints = initialdesign;

% Set constraints
Constraints.Ltarget = Ltarget;          % Target inductance to achieve
Constraints.Ldeviation = 0.01;          % Deviation from target allowed in percent
Constraints.Penalty = 100;              % Penalty for not achieving
Constraints.IntConstr = IntConstr;      % Specify integer constraint on NumTurns

poolobj = gcp;

Starting parallel pool (parpool) using the 'Processes' profile ...
Connected to parallel pool with 6 workers.

optimdesign = optimizeInductorSurrogate(Design,AnalysisParams,OptimParams,Constraints);

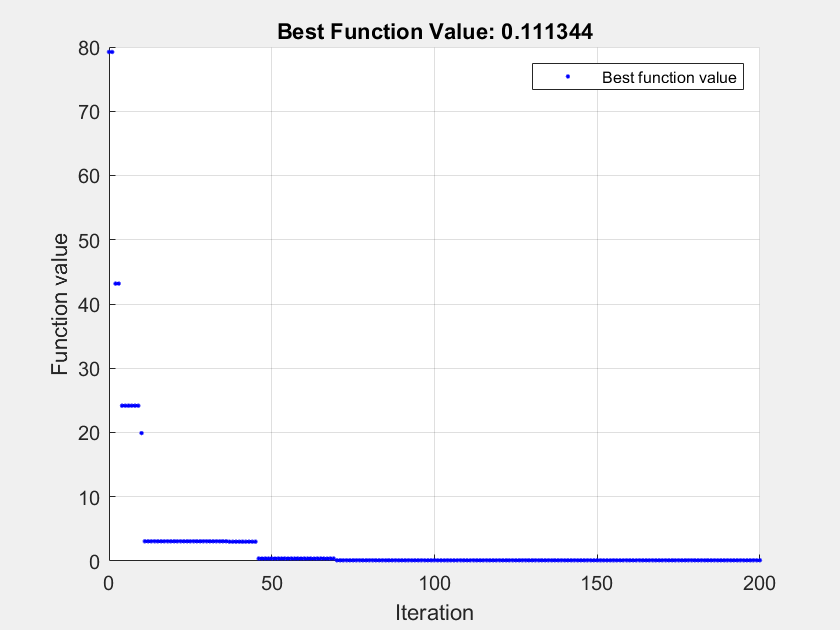
surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

Visualize Optimized Component and Compute Inductance

Assign the values returned by the optimization routine for the variables and recompute the inductance realized by the component at the center frequency

for q = 1:numel(optimVarIndx)
    component.(designVars{optimVarIndx(q)}) = optimdesign(q);
end
figure
show(component)

Loptimized = inductance(component,fc)

Loptimized = 1.0111e-08

Compare Initial and Optimized Design

Comparing the initial design guesses and the final optimized design values shows significant change to 3 of the 4 properties chosen. Note in particular the increase in the number of turns from 3 to 7. The inductance target is achieved to within 1% of error.

componentparam =  designVars(optimVarIndx);        
initialdesign = [initialdesign';Linitial/nH];
optimdesign = [optimdesign';Loptimized/nH];
designComparison = table(initialdesign,optimdesign,'RowNames',[componentparam;{'Inductance (nH)'}])

designComparison=5×2 table
                       initialdesign    optimdesign
                       _____________    ___________

    InnerDiameter          7e-05        7.2969e-05 
    Width                  3e-06        6.2813e-06 
    Spacing                2e-06        5.5938e-06 
    NumTurns                   3                 7 
    Inductance (nH)       2.1775            10.111 

Reference

1. Tuan Huu Bui, "Design and Optimization of a 10 nH Square-Spiral Inductor for Si RF Ics", University of North Carolina at Charlotte, October, 1999