value
Description
rcsval = value(rcssig,az,el,freq)rcsval, of the radar cross-section (RCS) specified
by the radar signature object, rcssig, computed at the specified
azimuth az, elevation el, and frequency
freq. If the specified azimuth and elevation is outside of the region
in which the RCS signature is defined, the RCS value, rcsval, is
returned as -Inf in dBsm.
Input Arguments
Output Arguments
Examples
Algorithms
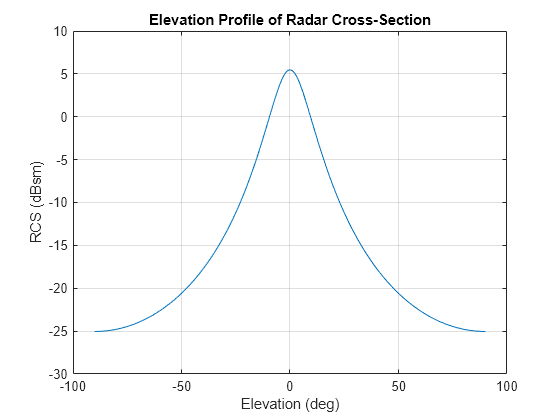
The RCS signature, is first linearly interpolated at the specified azimuth,
az, and elevation, el, view angles for the
provided frequencies, freq. The interpolated signature is then used as an
expected value of a probability distribution that generates a signature pattern value
according to the RCS fluctuation model specified by the FluctuationModel
property.. az and el are specified in degrees and
are defined in the body frame of the pattern. freq is in hertz.
If FluctuationModel is 'Swerling0', the returned
pattern value is a deterministic constant equal to the interpolated signature.
If FluctuationModel is 'Swerling1', the returned
pattern value is a random variable distributed according to an exponential distribution with a
mean value equal to the interpolated signature.
If FluctuationModel is 'Swerling3', the returned
pattern value is a random variable distributed according to a chi-square distribution with
four degrees of freedom and a mean value equal to the interpolated signature.
Extended Capabilities
Version History
Introduced in R2021a