faultBands
Generate fault frequency bands for spectral feature extraction
Syntax
Description
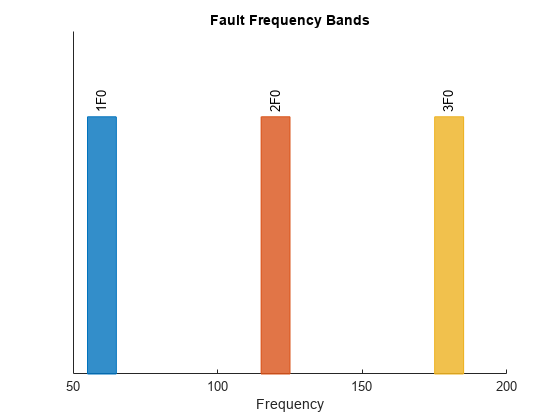
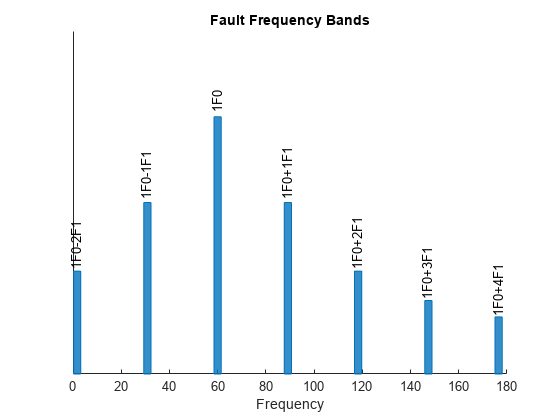
FB = faultBands(F0,N0,F1,N1)FB, using the distance of the first
sideband F1 from the fundamental frequency F0.
N1 is the array of the sidebands around F0. If
F1 is not specified, then faultBands sets
F1 to 10 percent of F0 by default.
N1 is equivalent to the 'Sidebands' name-value
pair. You can use the 'Type' name-value pair to specify separation
between successive sidebands.
___ = faultBands(___,Name,Value) allows
you to specify additional parameters using one or more name-value pair arguments.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Version History
Introduced in R2019b